Тема 9. Розгортки поверхонь
-
Розгортки гранних поверхонь
Кожна грань гранної поверхні представляє собою плоску фігуру, визначивши одним із розглянутих вище способів натуральні величини всіх граней необхідно побудувати їх на кресленику в тій чи іншій композиції.
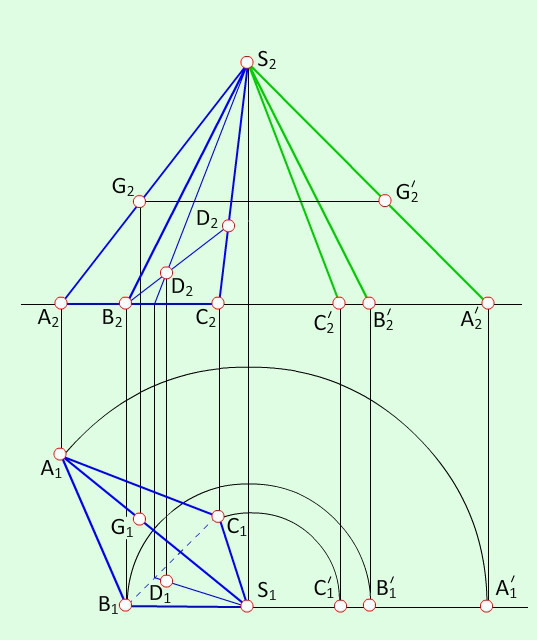
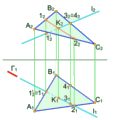
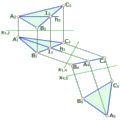
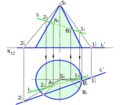
Нехай потрібно побудувати розгортку повної поверхні піраміди (рис. 9.1). За такого розміщення піраміди на площину П1 її основа спроекціюється в натуральну величину. Щоб визначити натуральну величину бокових граней, потрібно знайти дійсну довжину (натуральну величину) кожного бокового ребра. Для цього скористаємося обертанням ребер навколо осі і, що проходить через вершину піраміди перпендикулярно до площини П1.
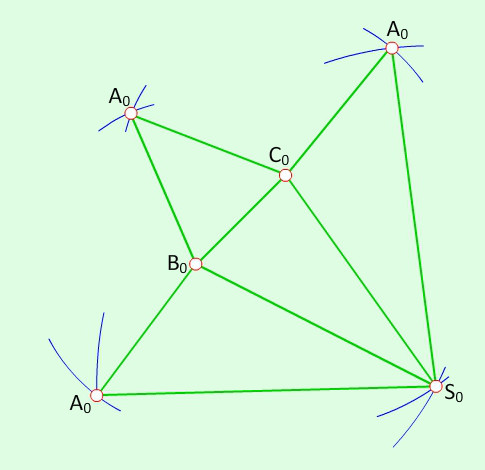
Рис. 9.1, а
Рис. 9.1, б
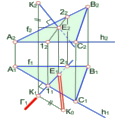
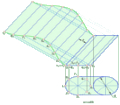
Як відомо, найменшою відстанню між двома точками є пряма. Якщо на поверхні задано дві точки які потрібно сполучити найкоротшою лінією, яка має назву геодезичної, то спочатку будують розгортку такої поверхні, наносять на неї задані точки, сполучають їх прямою, а потім результат переносять на поверхню.
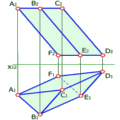
Нехай на піраміді задані точки G i D. Потрібно побудувати їх на розгортці та визначити найкоротшу відстань між ними по поверхні піраміди. Так як точка G розміщена на ребрі AS, потрібно при визначенні його натуральної величини перенести й точку G, тоді відстань від цієї точки до вершини спроекціюється на площину П2 в натуральну величину (S2G2=SG). Відклавши отриманий відрізок на прямій AS, отримаємо шукану точку G. Точку D можна перенести на розгортку за допомогою прямих, що проходять через неї, наприклад FS i BE. На перетині цих прямих на розгортці знайдемо точку D. З’єднавши прямою лінією точки G i D на розгортці отримаємо на ребрі SВ проміжну точку H геодезичної лінії.
Нехай на піраміді задані точки G i D. Потрібно побудувати їх на розгортці та визначити найкоротшу відстань між ними по поверхні піраміди. Так як точка G розміщена на ребрі AS, потрібно при визначенні його натуральної величини перенести й точку G, тоді відстань від цієї точки до вершини спроекціюється на площину П2 в натуральну величину (S2G2=SG). Відклавши отриманий відрізок на прямій AS, отримаємо шукану точку G. Точку D можна перенести на розгортку за допомогою прямих, що проходять через неї, наприклад FS i BE. На перетині цих прямих на розгортці знайдемо точку D. З’єднавши прямою лінією точки G i D на розгортці отримаємо на ребрі SВ проміжну точку H геодезичної лінії.