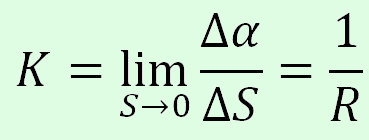• Плоскі криві. Криві другого порядку

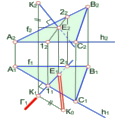
     Криву лінію можна розглянути як траєкторію точки, що рухається за певним законом, або як наслідок перетину кривих поверхонь. В інженерній графіці криві вивчають за їхніми проекціями.

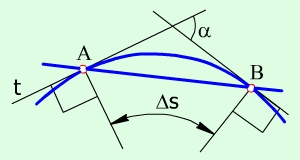
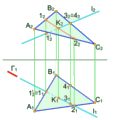
Рис. 7.1

     Викривленість кривої характеризується кривиною:

     Кривина є величиною оберненою до радіуса кола кривини R, проведеною через три точки дві з яких нескінченно близькі до третьої, яка розміщена між ними.
Єдиною кривою сталої кривини є коло.
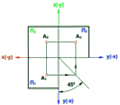
Множина нормалей до плоскої кривої утворює жмуток, обвідною якого є крива, що називається - еволютою (рис. 7.2).

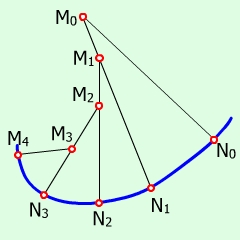
Рис. 7.2

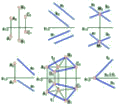
     Крива відносно своєї еволюти називається евольвентою. Форму евольвенти кола мають бічні поверхні зубців деяких зубчатих коліс і шестерень (рис. 7.3).

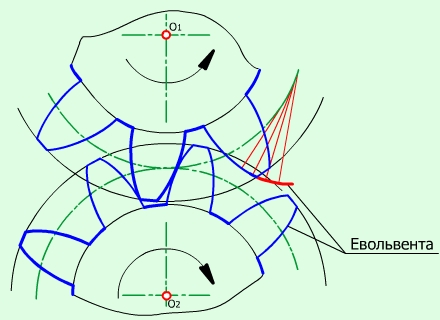
Рис. 7.3

     Кривинами другого порядку є еліпс, гіпербола, парабола та коло, які найбільш поширені в різних галузях техніки. Оскільки їх можна одержати в результаті перерізу конуса площиною, вони ще звуться конічними перерізами.
Еліпсом називається множина точок площини, сума відстаней від кожної з яких до двох даних точок (фокусів) є величиною сталою та дорівнює 2а (рис. 7.4).

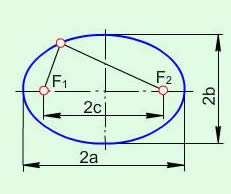
Рис. 7.4

Рівняння еліпса має вигляд:

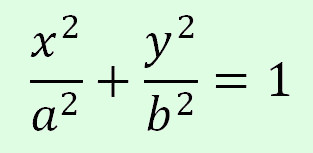
де .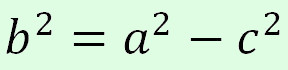

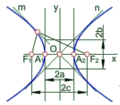
Гіперболою називається множина точок різниця відстаней яких до двох даних точок (фокусів) є величиною сталою та дорівнює 2с (рис. 7.5).

Гіпербола має також дві осі (х – дійсна, у – уявна) та дві асимптоти m,і n – прямі.



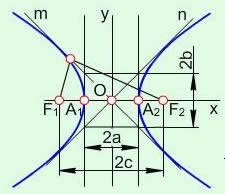
Рис. 7.5

Рівняння гіперболи:

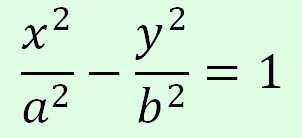
де .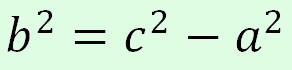

Парабола є геометричною множиною точок на площині, рівновіддалених від заданої точки (фокуса) (рис. 7.6). Рівняння параболи в прямокутних декартових координатах:

.

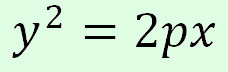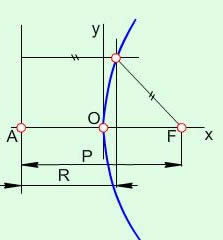
Рис. 7.6

• Просторові криві лінії
• Криві поверхні. Способи їх утворення
• Перелік тем