• Точка та пряма

     Метричні задачі – це задачі на визначення значень геометричних величин (довжин відрізків, кутів, відстаней).
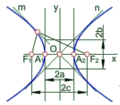
При частковому положенні прямої відстань від точки до прямої може проекціюватися на одну з площин проекції у натуральну величину. Тобто, якщо пряма є горизонтально-проекціюючою, то відстань від точки до прямої на горизонтальній площині проекцій П1 проекціюється в натуральну величину (рис.2.9,а), відповідно якщо пряма є фронтально-проекціюючою – натуральна величина відстані від точки до прямої проекціюється на полі П2.
Відстань від точки до прямої проекціюється в натуральну величину на полі П1, якщо площина, що задана точкою та прямою, є горизонтальною площиною рівня, аналогічно для фронтальної площини проекції.

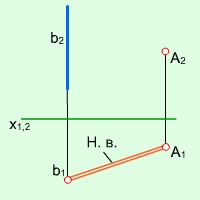
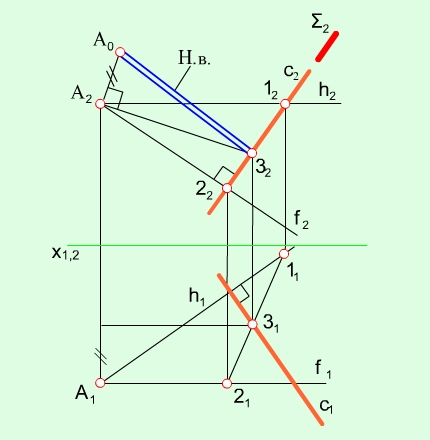
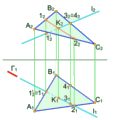
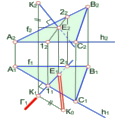
     Для визначення відстані від точки А до прямої с загального положення необхідно виконати такі побудови:
1) через точку А проводять площину, перпендикулярну до прямої с (рис.2.10);
2) через пряму с проводять фронтально-проекціюючу площину E;
3) точки перетину площини E з горизонталлю h та фронталлю f опускаємо на відповідні проекції горизонталі та фронталі в площині П1;
4) проводимо слід площини E;
5) знаходимо точку перетину В сліду 1-2 та прямої с;
6) за правилом прямокутного трикутника знаходимо натуральну величину (н. в.) відрізка АВ..

• Дві прямі
• Пряма та площина
• Точка та площина
• Дві площини
• Перелік тем