LABORATORY WORK № 13

INVESTIGATION OF STEPPER MOTOR. RESONANCE

13.1. Objectives

Analyze characteristics of stepper motor using different connection and control modes.

 

13.2. Task

Use experimental investigation to obtain maximum rotation speed and other characteristics of different stepper motor connection modes – unipolar and bipolar. Test and examine successive control modes:

·          full step;

·          wave;

·          half step;

·          break.

 

13.3. Resonance

At specific step rates stepper motors often experience an undesired reaction called resonance. The indications are a sudden loss of torque with possible skipped steps and loss of synchronization. Resonance is inherent in the design and operation of all step-ping motors. Slow stepping rates combined with high rotor inertia and elevated torque produce ringing as the rotor overshoots its de-sired angular displacement and is pulled back into position. Resonance arises when the step rate coincides with rotor ringing, typically about 100 to 200 steps/sec. Unable to overcome the combined effects of both load inertia and ringing, the motor skips steps and loses torque and synchronization. The resonant frequency of the stepper motor rotor depends on the amplitude of the oscillation, but as the amplitude decreases, the resonant frequency rises to a well-defined small-amplitude frequency. This frequency depends on the step angle and on the ratio of the holding torque to the moment of inertia of the rotor. Either a higher torque or a lower moment will increase the frequency. Formally, the small-amplitude resonance can be computed as follows: First, recall Newton’s law for angular acceleration:

 

                                                          (13.1)

 

where: T – torque applied to rotor; µ – moment of inertia of rotor and load, A – angular acceleration [rad/s]. For small amplitudes, the torque on the rotor can be approximated as a linear function of the displacement from the equilibriun position. Therefore, Hooke’s law is applied:

 

                                                      (13.2)

 

where: k – the «spring constant» of the system, in torque units per radian; – angular position of rotor [rad].

From (13.1) and (13.2) is solution of the resonant frequency f as function of k and µ is:

 

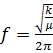                                                       (13.3)

 

It is very important, that moment of inertia of the rotor plus any coupled load matters, so the resonant frequency depends on the load. In practice, this oscillation can cause significant problems when stepping rate is anywhere near a resonant frequency of the system – random and uncontrollable motion can appear.

Changing any one of the three parameters – inertia load, step rate, or torque – will reduce or eliminate resonance. As a practical matter, only torque is the easiest to change using a technique called micro-stepping. Micro-stepping applies power to the stator windings of the mo-tor in incremental steps. Torque builds slowly reducing overshoot and canceling resonance.

 

Time Constant

Because of motor winding inductance, the current will not increase or decrease instantaneously. If a voltage V is connected to a winding with the resistance Rand inductance L, the current in-creases exponentially:

 

                                                    (13.4)

 

Value L / R is called time constant and indicates time needed for the current to rise up to 63 % of the final value i = V / R. For the equipment motor with R = 2.5 and L = 8 mH used in laboratory the time constant τ = L / R = 3.2 ms. It means, the step switching frequency is limited to about 200 steps per second. There is a way to increase maximal rotation speed: time constant τ can be decreased sing additional series connected resistor (increasing R) and accord ingly increased supply voltage to reach the normal motor current. If the 10 resistor added and supply voltage increased to 25 V, τ = 0.64 ms, and 1000 steps per second speed can be reached.

 

The Workflow

The laboratory equipment for the stepper motor investigation – TERCO SD1664-1 Stepper motor trainer is shown in Fig. 13.1. It consists of a motor block with adjustable load on the left, and control block in the centre. Closer view of control measurement part is presented in Fig. 13.2. The oscilloscope for voltage form monitoring and voltmeter for coil current measurement are necessary.

 

Fig. 13.1. Stepper motor TERCO SD1664-1

 

Measurement equipment connection

 

Fig. 13.2. Measurement part of stepper motor train

 

13.4. Method of testing

Maximum pull-in, pull-out and torque characteristic measurement.

1.       Set «Speed» potentiometer to the minimum value. Turn down the adjusting screw until the braking cord is loose. Switch «Instrument selector» to torque mode (Nm), adjust zero on display by «Zero setting torque» potentiometer (Fig. 13.1).

2.       Switch «Instrument selector» to frequency mode (Hz), select «Unipolar» in driver section and «Normal» in «Program selector».

3.       Start the motor at very low speed, stop and restart the motor (use the Hold/Run switch). Increase the frequency until the motor does not start properly and write the frequency value into table 13.1.

4.       Adjust three different torque values in range 0 – 1 Nm, and re-peat procedure 3.

5.       Repeat steps 3 and 4 for bipolar mode.

6.       Repeat steps 3 – 5 using one and two additional weights on motor shaft, fill in the results into table 13.1.

7.       Measure the maximum pull-in torque: loose the braking cord; select «Unipolar» in driver section and «Normal» in «Program selector»; set the operational frequency 20 Hz; increase the torque and try to restart the motor. Proceed until the motor cannot start, and write down the obtained torque value in table 13.2.

8.       Repeat step 7 for 50 Hz, 100 Hz, 200 Hz, 400 Hz, 600 Hz and 800 Hz operational frequency and write down the data in table 13.2.

9.       Repeat steps 7 and 8 using bipolar conection mode.

10.  Measure the maximum pull-out torque: loose the braking cord; select «Unipolar» in driver section and «Normal» in «Program selector»; set the operational frequency 20 Hz; run the motor and increase the torque. Proceed until the motor stops, and write down the obtained torque value in table 13.2.

11.  Repeat step 10 for 50 Hz, 100 Hz, 200 Hz, 400 Hz, 600 Hz and 800 Hz operational frequency and write down the data in table 13.2.

12.  Repeat steps 10 and 11 using bipolar conection mode.

 

 

Table 13.1.

The maximum pull-out rate

Weight No	Load, Nm	Frequency, Nz
		Unipolar	Bipolar

 

 

Table 13.2.

The maximum pull-in and pull-out torq

Mode	Maximum torque, Nm
	20 Hz	50 Hz	100 Hz	200 Hz	400 Hz	600 Hz	800 Hz
Pull-in unipolar
Pull-in bipolar
Pull-out unipolar
Pull-out bipolar

 

 

13.5. Content of Report

1.       Objective, task and motor parameters of the laboratory work.

2.       Work results for Experiment 1 – table with maximum rotation speed achieved using different connection and control modes; control pulse and coil voltage oscillograms, coil current de-pendence from pulse frequency for the offered control mode, ramping diagram.

3.       Work results for Experiment 2: maximum pull-out, resonance and maximum pull-in frequency values for both unipolar and bipolar connection modes of unloaded motor and with addition-al load.

4.       Work results for Experiment 3: maximum pull-in and pull-out rates (Table 13.1) and torques (Table 13.2) for different operation modes.

5.       Conclusions.

 

13.6. Control questions

1.       Enumerate advantages and drawbacks of stepper motors.

2.       What are the main connection types for stepper motors?

3.       How do the parameters depend on connection type?

4.       What are control modes for stepper motors?

5.       What control mode can achieve maximum rotation speed?

6.       What is the speed resonance and how to avoid it?

7.       What is the back-phasing mode?

8.       Explain the ramp mode using the diagram.

9.       How to find the maximum pull-in and pull-out frequency?

10.  How to find the maximum pull-in and pull-out torque?