LABORATORY WORK №10

DEVELOPMENT OF EQUIVALENT CIRCUITS

1.1.         Objectives

Get acquainted with starting transients of the current and velocity of the squirrel-cage induction motor.

 

1.2.             Tasks

1.       Experimentally obtain starting transients of motor phase cur-rent at no load.

2.       Experimentally obtain starting transients of motor speed at no load.

 

1.3.         Development of equivalent circuits

The three-phase induction motor is represented by a stationary equivalent circuit.

Considering the rotor first and recognizing that the frequency of rotor currents is the slip frequency, we may express the per-phase rotor leakage reactance  at a slip s in terms of the standstill per phase reactance :

 

                                                          (10.1)

 

Next we observe that the magnitude of the voltage induced in the rotor circuit is also proportional to the slip.

A justification of this statement follows from transformer theory because we may view the induction motor at standstill as a transformer with an air gap. For the transformer, we know that the induced voltage, say , is given by:

 

                                                  (10.2)

 

But at a slip s, the frequency becomes sf. Substituting this value of frequency for Eq. (10.2) yields the voltage at a slip s as:

 

=                                        (10.3)

 

If  is the per-phase voltage induced in the rotor at standstill, then the voltage at a slip s is given by:

 

                                                        (10.4)

 

Using Eqs. (10.3) and (10.4), we obtain the rotor equivalent circuit shown in Fig. 10.1 a. The rotor current  is given by:

 

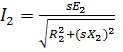                                                (10.5)

 

which may be rewritten as:

 

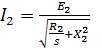                                                  (10.6)

 

resulting in the alternative form of the equivalent circuit shown in Fig. 10.1 b. Notice that these circuits are drawn on a per-phase basis. To this circuit we may now add the per-phase stator equivalent circuit to obtain the complete equivalent circuit of the induction mo-tor.

In an induction motor, only the stator is connected to the ac source. The rotor is not generally connected to an external source, and rotor voltage and current are produced by induction. In this regard, as mentioned earlier, the induction motor may be viewed as a transformer with an air gap, having a variable resistance in the secondary. Thus, we may consider that the primary of the trans-former corresponds to the stator of the induction motor, whereas the secondary corresponds to the rotor on a per-phase basis. Because of the air gap, however, the value of the magnetizing reactance X_m tends to be relatively low, compared to that of a transformer. As in a transformer, we have a mutual flux linking both the stator and the rotor, represented by the magnetizing reactance and various leakage fluxes. For instance, the total rotor leakage flux is denoted by X₂ in Fig. 10.1.

 

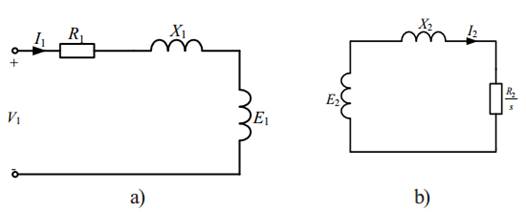
Fig. 10.1. Stator and rotor as coupled circuits

 

Now considering that the rotor is coupled to the stator as the secondary of a transformer is coupled to its primary, we draw the circuit shown in Fig. 10.2.

Fig. 10.2. Two forms of rotor equivalent circuit

 

To develop this circuit further, we need to express the rotor quantities as referred to the stator. However, having referred the rotor quantities to stator, we obtain from the circuit given in Fig. 10.2 the exact equivalent circuit (per phase) shown in Fig. 10.3.

 

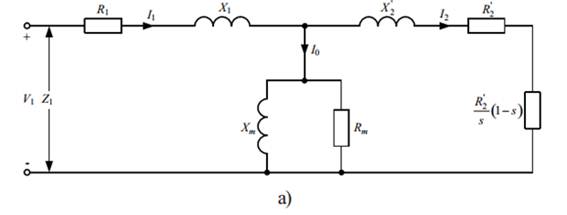
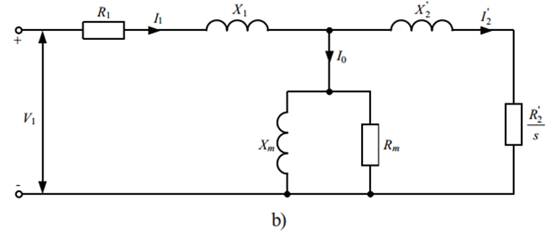
Fig. 10.3. Two forms of equivalent per phase circuit of induction motor

 

Performance criteria of induction motors

The performance of an induction motor may be characterized by the following major factors: locked rotor torque and current, pull up torque, breakdown torque and percent slip. In addition, full-load torque and current must be considered when evaluating an application.

Locked Rotor Torque. Locked rotor torque, also referred to as starting torque, is developed when the rotor is held at rest with the rated voltage and frequency applied. This condition occurs each time the motor is started. When the rated voltage and frequency are applied to the stator there is a brief amount of time before the rotor turns.

Locked Rotor Current. Locked rotor current is also referred to as starting current. This is the current taken from the supply line at the rated voltage and frequency with the rotor at rest.

Pull Up Torque. Pull up torque is the torque developed during acceleration from start to the point breakdown torque occurs.

Breakdown Torque. Breakdown torque is the maximum torque a motor develops at the rated voltage and speed without an abrupt loss of speed.

Full-Load Torque. Full-load torque is the torque developed when the motor is operating with the rated voltage. A typical torque-slip curve is presented in Fig. 10.4. Locked rotor torque (at standstill) is greater than full load torque and the motor can be started at full load. Its speed increases and rotor reaches speed determined by load, frequency and load.

Full-Load Current. Full-load current is the current taken from the supply line at rated voltage, frequency and load. Three-phase AC motors, for example, typically requires 600 % starting current and 150 % starting torque.

 

 

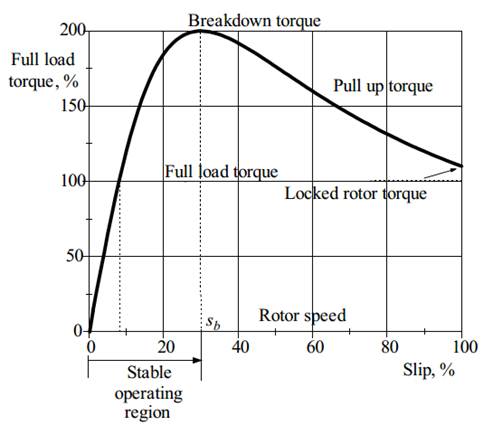
Fig. 10.4. A typical torque-slip curve

 

1.4.         Method of testing

1.       Measurement of current transient .

2.       Connect the circuit shown in Fig. 10.5.

 

 

Fig. 10.5. Electrical circuit for measurement of current and speed

Transients

3.       Switch on and adjust the oscilloscope.

4.       Switch on the induction motor and get the curve of current transient in the screen.

5.       Measurement of speed transient .

6.       Connect the oscilloscope to the terminals of tachogenerator BR load resistor.

7.       Switch on and adjust the oscilloscope.

8.       Switch on the induction motor and get the curve, proportional to rotational speed of motor.

9.       Calculate electromechanical time constant from the obtained curve.

 

 

1.5.         Content of report

1.       Task of the work and experimental circuit.

2.       Experimental curve of current starting transients.

3.       Experimental curve of speed starting transients.

4.       Calculation of electro-mechanical time constant from speed starting transient curve.

5.       Conclusions.

 

1.6.         Control questions

1.       Explain what elements are denoted as QF, PA, PV, TA, BR in the electrical circuit.

2.       What is called electromechanical time constant?

3.       How can you find value of electromechanical speed constant from the speed transient curve?

4.       What current is measure red by ammeter PA?

5.       What will happen if resistance TA will be turned off?

6.       For what purpose is tachogenerator BR used in the circuit?