1. Утворення енергетичних зон в твердих тілах

Зонна теорія твердого тіла дозволяє не лише пояснювати, але й передбачати, як радикально можна змінювати фізичні властивості твердих тіл. Енергетичний спектр електронів ізольованих атомів суттєво змінюється при утворенні з них твердого тіла. Під час зближення двох сусідніх атомів їх електронні оболонки зазнають перекриття. В результаті чого різко змінюється характер руху електронів: електрони, які знаходились на визначеному рівні ізольованого атома, отримують можливість для переходу без втрати енергії на відповідний рівень сусіднього атома і таким чином вільно рухатись твердим тілом. Утворення твердого тіла можна уявити собі як зближення великого числа N ізольованих атомів. Замість

одного однакового для всіх атомів рівня виникає N дуже близьких густо розміщених рівнів, які утворюють відповідну енергетичну зону. Кожна така зона являє собою відповідний розщеплений енергетичний рівень ізольованого атома, на якому може знаходитись 2(2l+1) електронів (l – орбітальне квантове число). На s – рівні.(l=0) може бути 2 електрона, на p – рівні (l=1) 6 електронів, на d (l=2) 10 електронів і т.д.. В результаті зближення атомів замість окремих рівнів , , , , , утворюються відповідні енергетичні зони: 1s, 2s, 2p, 3s, 3p, 3d…(див. рис.1).

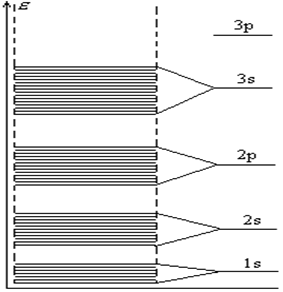
Рис. 1. Утворення енергетичних зон в твердому тілі

Кожна така зона має N енергетичних рівнів, а число електронів, енергії яких утворюють дану зону, може бути не більшим, ніж 2N для s – зон, 6N для p – зон, 10 N для d – зон і т.д. Отже, кожному рівню ізольованого атома в кристалі відповідає зона дозволених енергій. Зони дозволених енергій розділені між собою областями заборонених енергій – забороненими зонами …(див рис. 2). Із збільшенням енергії електрона в атомі ширина дозволених зон збільшується, а заборонених – зменшується. Це пояснюється тим, що електрони зовнішніх оболонок взаємодіють сильніше, ніж внутрішніх. Глибокі внутрішні рівні атомів при утворені кристалу майже зовсім не розщеплюються і залишаються такими вузькими, як і в атомах. Відповідно до цього ширина заборонених зон зменшується із зростанням енергії. Ширина енергетичних зон залежить від віддалі між атомами (сталої гратки) і не залежить від розмірів кристалу.

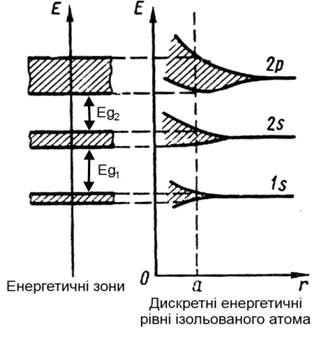
Рис. 2. Розщеплення енергетичних рівнів ізольованих атомів при утворені кристалу

Подібно до того, як і в ізольованому атомі, так і в кристалі електрони можуть переходити з одного рівня на інший, можливі також переходи з однієї дозволеної зони в іншу або в середині тієї ж зони. Фізичні властивості твердого тіла визначаються взаємним розміщенням різним енергетичних зон і розподілом електронів в них. В ізольованому атомі внутрішні енергетичні рівні повністю заповнені електронами, частково заповненим може бути лише зовнішній рівень, який називається рівнем валентних електронів. Тому зона, яка утворилась із енергетичних рівнів валентних електронів називають валентною. Ця зона може бути частково або повністю заповненою електронами, залежно від того, на скільки заповнений електронами валентний рівень ізольованих атомів. Вище валентного рівня за шкалою енергій знаходяться інші рівні, які вільні від електронів. Ці рівні можна заповнити, збудивши електрони валентного рівня. Аналогічна картина спостерігається і в кристалі. Вище валентної зони (V – зони) розміщена повністю вільна від електронів зона, яку називають зоною провідності (C – зона).

З точки зору зонної теорії різниця електричних властивостей твердих тіл визначається двома причинами: 1) взаємним розміщенням зони провідності і валентної; 2) ступенем їх заповнення електронами. Поділ твердих тіл на провідники, напівпровідники та діелектрики (ізолятори) в першу чергу визначається ступенем заповнення валентної зони. Якщо валентна зона заповнена не повністю, то кристал є провідником (рис. 3 а). Але й також провідником може бути такий кристал, в якому валентна зона заповнена повністю і перекривається із зоною провідності (рис. 3 б). Якщо в кристалі валентна зона повністю заповнена електронами та відділена від зони провідності забороненою зоною шириною від 0,1 до 3 еВ, то такий кристал відноситься до напівпровідників (рис. 3 в). Якщо ширина забороненої зони більша 3 еВ, то речовина буде діелектриком (рис. 3 г).

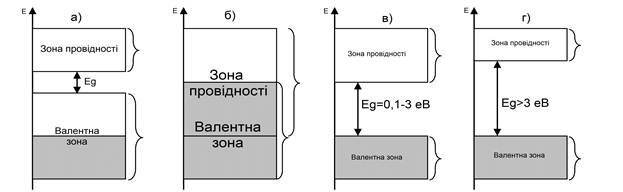
Рис.3. Схема можливого взаємного розміщення зон та їх заповнення електронами в

твердому тілі

Розглянуті вище положення зонної теорії стосуються ідеальних кристалів. В реальних кристалах завжди існують порушення періодичності потенціалу кристалічної гратки, викликані різними домішками, вакантними вузлами, міжвузловими атомами, дислокаціями, гранями мікрокристалів, коливаннями атомів (фононами) та ін. Це обумовлено, по – перше, технологічними труднощами при отриманні кристалів і, по – друге, цілеспрямованим створенням дефектів для надання речовині заданих властивостей. Різні дефекти можуть суттєво впливати на зонну структуру кристалів, а отже, і на їх фізичні властивості. Якщо в кристалі є дефект, то його електричне поле може захоплювати електрон. Такий локалізований поблизу дефекту електрон має енергію, що попадає в заборонену зону, а в енергетичному спектрі кристалу появляється набір локальних рівнів в забороненій для ідеального кристалу зоні. Ці рівні називаються локальними, бо вони виникають в місцях розміщення дефектів. Наявність таких рівнів суттєво впливає на електропровідність, оптичне поглинання, люмінісценсію та інші явища в напівпровідниках та діелектриках. Для металів дефекти гратки виконують роль, як правило, додаткових центрів розсіяння для електронів. Якщо енергетичні рівні дефектів здатні віддавати в зону провідності електрони, то їх називають донорними, а самі дефекти – донорами. Мінімальна енергія, яку необхідно надати електрону донорного рівня, щоб перевести його в зону провідності називається енергією іонізації донора. Якщо енергетичні рівні дефектів здатні приймати електрони із валентної зони, то їх називають акцепторними, а відповідні дефекти – акцепторами. Мінімальна енергія, яку необхідно надати електрону валентної зони, щоб збудити його на акцепторний рівень, називається енергією іонізації акцептора. Існують також дефекти, які проявляють амфотерні властивості, тобто вони можуть бути як донорами, так і акцепторами.

2. Поняття про ефективну масу електрона

Нехай на електрон, який рухається в періодичному полі кристалу, додатково діє деяка зовнішня сила . Якщо дана сила є достатньо малою, то електрони під її дією не будуть переходити з одної дозволеної зони в іншу, а будуть лише змінювати свій напрям руху, тобто хвильовий вектор . Так як класичне рівняння руху є справедливим для середніх квантовомеханічних значень величин, то закон збереження та зміни енергії має вигляд:

, (1)

де , а .

Тоді

, (2)

а сила

. (3)

Отже, квазіімпульс електрона в кристалі відіграє ту ж саму роль, що імпульс вільного електрона. Із виразу (3) слідує, що хвильовий вектор електрона не зберігається в часі при порушеннях періодичності потенціалу кристала . Під прискоренням електрона в кристалі розуміють швидкість зміни середньої квантовомеханічної швидкості , тобто

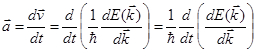. (4)

Для і – ої компоненти прискорення, де і=x,y,z,

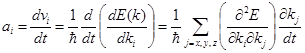. (5)

Тоді, згідно з (3),

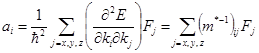. (6)

Сукупність дев’яти величин

(7)

називається тензором оберненої ефективної маси електрона в кристалі. Його можна також подати у вигляді матриці:

Враховуючи те, що , отримаєм

. (9)

Оскільки ,

то тензор оберненої ефективної маси є симетричним. При відповідному виборі осей системи координат даний тензор можна звести до діагонального виду:

Такі осі називаються головними осями тензора. Тензор, обернений тензорові оберненої ефективної маси, називається тензором ефективної маси . Якщо є діагональним, то

Для недіагонального тензора оберненої ефективної маси це несправедливо. Наприклад, для напівпровідникових кристалів кремнію та германію залежність енергії електрона від хвильового вектора являє собою еліпсоїд обертання, який характеризується трьома відмінними від 0 компонентами тензора ефективної маси та . Тут та ефективна маса вздовж та поперек головної осі еліпсоїда відповідно.

З’ясуємо, що дає введення поняття ефективної маси електрона в кристалі. Для спрощення розглянемо випадок, коли ефективна маса є скаляром, тобто . Тоді для зовнішньої сили маємо, що . З іншої сторони, згідно з другим законом Ньютона, з врахуванням внутрішніх сил ,

, (12)

де маса вільного електрона; компонента незалежних внутрішніх сил, тобто сил обумовлених потенціалом кристалу . З іншої сторони

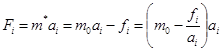, (13)

тобто .

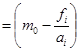Отже, незалежні внутрішні сили із сторони кристалічної гратки включені в означення тензора ефективної маси і ефективна маса електрона в кристалі може бути як більшою, так і меншою за масу вільного електрона, додатною та від’ємною. При цьому рух електрона в періодичному потенціалі кристалу формально можна звести до класичного руху вільного електрона під дією зовнішньої сили з цим же зарядом, але з масою, яка рівна ефективній.