1. Загальні властивості напівпровідників

До напівпровідників відносяться речовини, які за питомою електропровідністю займають проміжне місце між провідниками (металами) та діелектриками. Значення питомої електропровідності та питомого опору для цих трьох класів речовин представлено в таблиці 1.

Таблиці 1.

Питома електропровідність та питомий опір різних класів твердих речовин

Клас речовин	Питома електропровідність,	Питомий опір,
Провідники Напівпровідники Діелектрики	10^4 10^4 – 10^–10 <10^-10	<10^–4 10^-4 – 10^10 >10^10

Основною ознакою, яка виділяє напівпровідники серед інших речовин, є сильна залежність їх питомої електропровідності від температури та концентрації домішки. Так, наприклад, при збільшенні температури на 1⁰С питома електропровідність зростає на 5—6%. Провідність металів із збільшенням температури незначно зменшується (зменшення складає долі відсотка на 1⁰С). Введення домішок в напівпровідники в кількості 10^–7 – 10^–9 % вже суттєво збільшує їх електропровідність. У багатьох напівпровідників різка зміна питомої електропровідності виникає під час дії на них світла, іонізуючого випромінювання та інших факторів. До напівпровідників належить широкий клас речовин. Такі хімічні елементи, як бор, вуглець, кремній, сірка, германій, миш’як, селен, сіре олово, йод, телур, хімічні сполуки CuCl, CaAs, GeSi, CuO, PbS і також багато органічних сполук, мінералів – природних хімічних сполук належать до напівпровідників. В електроніці широко використовуються кремній, германій, арсенід галію, які є сировинним матеріалом для виготовлення багатьох напівпровідникових приладів. Бор, фосфор, миш’як і деякі інші речовини використовуються в якості домішок. Більшість напівпровідників, які використовуються в електроніці, мають монокристалічну структуру. Це означає, що по всьому об’єму такої речовини атоми розміщені в строго періодичній послідовності, на визначених сталих відстанях один від одного, утворюючи кристалічну гратку. У германія і кремнія кристалічна гратка має структуру алмаза: кожний атом оточений чотирма сусідами, які знаходяться у вершинах правильного тетраедра (рис. 1).

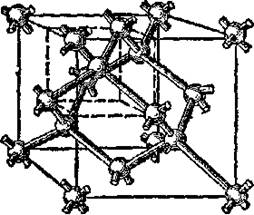
Рис. 1. Кристалічна гратка германія та кремнія

Кожний атом кристалічної гратки електрично нейтральний, але існують сили, які утримують атоми у вузлах гратки. Ці сили виникають за рахунок валентних електронів, які створюють ковалентний зв’язок. В германії та кремнії, які є чотирьохвалентними елементами, на зовнішній електронній оболонці знаходиться по чотири валентних електрона, тому кожен атом утворює чотири ковалентних зв’язки з чотирма найближчими сусідами. В ідеальній кристалічній гратці всі електрони зв’язані зі своїми атомами, тому така структура не проводить електричний струм. Під час нагрівання або опромінення частина електронів може відірватися від своїх атомів. Такі вільні від валентного зв’язку електрони можуть вільно переміщуватись по всьому кристалу, тому їх називають електронами провідності. Під час розриву валентного зв’язку утворюється вакантний стан (дірка), який має нескомпенсований позитивний заряд, який рівний за величиною зарядові електрона. Оскільки на незаповнений зв’язок за рахунок теплового руху можуть легко переходити електрони, то даний вакантний стан, в якому відсутній електрон, може легко переміщуватись по гратці. При наявності зовнішнього електричного поля дірка буде рухатись в напрямку вектора напруженості поля, тобто виникне електричний струм. Напівпровідник, який має у вузлах кристалічної гратки лише свої атоми називається власним. Для власного напівпровідника носіями струму є електрони і дірки. В електроніці часто використовують напівпровідники, в яких частина атомів основної речовини заміщена атомами іншої. Такі напівпровідники називають домішковими. Для германію і кремнію частіше всього використовуються п’ятивалентні (фосфор, сурма, миш’як) і трьохвалентні (бор, алюміній, індій, галій) домішки. При наявності п’ятивалентної домішки чотири валентних електрона домішкового атома спільно з чотирма валентними електронами сусідніх атомів утворюють ковалентні зв’язки, а п’ятий валентний електрон домішки виявляється “зайвим”. Енергія зв’язку його із сусіднім атомом набагато менша енергії необхідної для звільнення валентного електрона основної речовини, оскільки енергія іонізації домішки набагато менша ширини забороненої зони типових напівпровідників (табл. 2).

Таблица 2.

Значення енергії іонізації п’ятивалентних домішок в германії та кремнії

Домішка	Енергія іонізації домішки, еВ
	германій		кремній
Фосфор Миш’як Сурма	0.012 0,013 0,0096	0.044 0,049 0,039

Завдяки малості енергії іонізації п’ятий валентний електрон при кімнатній температурі (при Т=300 К середня енергія теплового руху kT~ 0,026 еВ.), а то і меншій, враховуючи статистичний розподіл Максвелла – Больцмана, може бути відірваним від свого домішкового атома. При цьому утворюється електрон провідності і позитивно заряджений іон – атом домішки, який втратив даний електрон і буде коливатись навколо положення рівноваги. Такі домішки називаються донорними, а такі леговані напівпровідники матимуть електронний тип провідності (n – тип).

При введені в кристал трьохвалентної домішки домішковий атом віддає три своїх валентних електрона для утворення ковалентного зв’язку з трьома найблищими сусідніми атомами. Зв’язок з четвертим атомом виявляється незаповненим, але на нього можуть порівняно легко переходити валентні електрони атомів основної речовини, оскільки енергія іонізації троьохвалентної домішки, як і п’ятивалентної, набагато менша за ширину забороненої зони напівпровідника (Табл. 3).

Таблиця 3.

Значення енергії іонізації трьохвалентних домішок в германії та кремнії

Домішка	Енергія іонізації домішки, еВ
	германій		кремній
Бор Алюміній Галій Індій	0,0104 0,0102 0,0108 0,0112	0,045 0,057 0,065 0,160

У разі переходу валентного електрона на незаповнений зв’язок, домішковий атом разом з даним приєднаним електроном утворюватиме негативно заряджений іон, який коливатиметься навколо свого положення рівноваги. При цьому утвориться дірка, яка вільно може рухатись по всьому кристалу. Домішки, які захоплюють електрони, називаються акцепторними, а такі напівпровідники матимуть дірковий тип провідності (p – тип).

2. Концентрація електронів та дірок для невиродженого напівпровідника

В адіабатному наближені вважається, що тепловий рух атомів кристалічної гратки впливає на ймовірність заповнення носіями заряду квантових станів в дозволених зонах, але не на самі стани. В напівпровідниках, так як і в металах, ймовірність заповнення електроном енергетичного рівня з енергією визначається функцією Фермі – Дірака:

, (1)

де – хімічний потенціал або рівень Фермі. Дану функцію розподілу використовувати можна лише для рівноважних носіїв заряду, що і позначають знаком “0”. Із (1) слідує, що при T=0 K⁰ всі енергетичні рівні з енергією заповнені електронами , а при енергетичні рівні вільні від електронів . При T>0 K⁰ “сходинка” в функції розподілу розмивається і з’являється “хвіст” кривої розподілу (рис. 2).

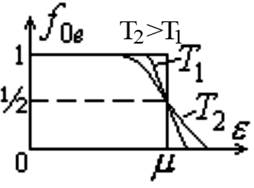
Рис. 2. Залежність функції Фермі – Дірака від енергії

При температурі T>0 K⁰ ймовірність заповнення рівня з енергією, згідно з (1), рівна ½. Отже, рівень хімічного потенціалу (рівень Фермі) – це такий рівень, який може з однаковою ймовірністю бути заповнений електронами або бути вільним від них. Функція розподілу Фермі – Дірака для дірок матиме вигляд:

. (2)

Число електронів , які знаходяться в одиничному об’ємі кристалу, енергії яких лежать в інтервалі від до буде визначатись ймовірностями заповнення електронами енергетичних рівнів (функцією Фермі – Дірака) та числом можливих квантових станів в даному інтервалі енергій:

. (3)

Двійка у виразі (3) враховує спін електрона.

Для сферичної ізоенергетичної поверхні число квантових станів, які можуть займати електрони кристалу одиничного об’єму з

енергією від до (див. рис. 3)рівне:

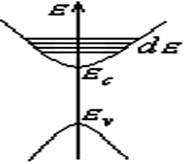
Рис. 3. Заповнення електронами квантових станів зони провідності

, (4)

де ефективна маса густини станів для електронів провідності. Також вводять поняття “функції густини станів” для електронів зони провідності:

. (5)

Дана функція визначає число квантових станів в кристалі одиничного обʼєму, які знаходяться в одиничному інтервалі енергій. Як видно з (5), густина станів збільшується при збільшенні енергії та ефективної маси електронів. Для дірок валентної зони функція густини станів має вигляд:

, (6)

де ефективна маса густини станів для дірок.

У непрямозонних напівпровідниках до яких належать, наприклад, германій та кремній, дно зони провідності є складним і характеризується трьома компонентами тензора ефективної маси: . В цьому випадку вираз для функції густини станів має аналогічний вигляд, але під ефективною масою густини станів у виразі (5) треба розуміти таку величину:

, (7)

де M – число еквівалентних мінімумів (долин). Для кремнію M=6, а для германію M=4. Враховуючи вирази (3) та (4),

. (8)

Розглянемо спочатку випадок, коли . Тоді

. (9)

Для даного випадку електронний газ в зоні провідності описується класичною статистикою Максвелла – Больцмана. Напівпровідники, для яких рівноважні носії заряду підлягають цій статистиці називаються невиродженими. Умова має виконуватись для всіх енергій електрона, в тому числі і для мінімальних енергій , тобто . Це дозволяє сформулювати висновок: в невироджених напівпровідниках рівень Фермі знаходиться нижче дна зони провідності на величину не меншу, ніж .

Концентрація всіх електронів буде рівна:

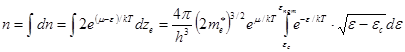. (10)

Так як підінтегральна функція швидко спадає, то верхню межу інтегрування можна замінити на нескінченість, тоді:

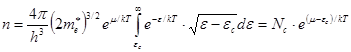, (11)

 – ефективна густина станів в зоні провідності,

яка чисельно рівна концентрації електронів в зоні провідності при умові, що рівень Фермі співпадає з дном зони провідності. Аналогічно можна отримати і вираз для концентрації дірок в невиродженому напівпровіднику:

, (12)

– ефективна густина станів у валентній зоні.

3. Концентрація носіїв заряду та рівень Фермі у власному напівпровіднику

У власному напівпровіднику носії заряду утворюються за рахунок збудження електронів з валентної зони в зону провідності. В таких напівпровідниках електрони і дірки утворюються в однаковій кількості. Концентрацію носіїв заряду у власному напівпровіднику будемо позначати так: , , . Для визначення концентрації власних носіїв заряду скористуємось формулами (11) та (12). Тоді ,

. (13)

Як слідує з (13), концентрація носіїв заряду у власному напівпровіднику зростає при збільшенні температури за експоненціальним законом. Відомо, що існує незначне зменшення за лінійним законом ширини забороненої зони напівпровідника при збільшенні температури:

(14)

– ширина забороненої зони при T=0 K⁰. Підставимо (14) в (13). Тоді

,

, (15)

, (16)

де , , . Тоді

.

Таким методом визначають ширину забороненої зони напівпровідника. Питома електропровідність власного напівпровідника

, (17)

де , рухливість електронів і дірок відповідно.

Знайдемо положення рівня Фермі (хімічного потенціалу) у власному напівпровіднику, враховуючи, що :

,

. (18)

Після математичних спрощень отримаємо, що

(19)

Із (19) слідує, що:

1. Якщо , то при всіх температурах .

2. Якщо , то при T=0 . Для даних двох випадків рівень Фермі буде знаходитись точно по середині забороненої зони (рис. 4, крива 1).

3. Якщо , то із збільшенням температури рівень Фермі піднімається вверх від середини забороненої зони (рис. 4, крива 2).

4. Якщо , то із збільшенням температури рівень Фермі опускається вниз від середини забороненої зони (рис. 4, крива 3).

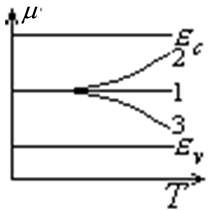
Рис. 4. Температурна залежність рівня Фермі для власного напівпровідника

4. Концентрація носіїв заряду та рівень Фермі у домішковому напівпровіднику з одним типом домішки

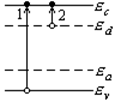Розглянемо для прикладу напівпровідник, який має мілкі донорні рівні одного типу. За рахунок теплового збудження в зоні провідності будуть утворюватись електрони, а у валентній зоні – дірки. Із зонної діаграми видно, що електрони утворюються при переходах 1 і 2, а дірки лише при переході 1. В такому напівпровіднику очевидно концентрація електронів буде більшою, ніж концентрація дірок. Для знаходження концентрації електронів використаємо закон діючих мас та рівняння електронейтральності.

1. Закон діючих мас.

Розглянемо добуток концентрацій носіїв заряду. Згідно з (11) та (12),

. (20)

Співвідношення (20) є законом діючих мас для носіїв заряду в напівпровіднику. Зауважимо, що для даного напівпровідника при фіксованій температурі . Із (20) слідує, що у разі збільшення концентрації електронів концентрація дірок зменшується. Якщо , то напівпровідник матиме електронний тип провідності ( – тип). Із збільшенням концентрації електронів, збільшується ймовірність зустрічі електронів з дірками і внаслідок рекомбінації дірки зникають частіше, ніж у випадку малих значень концентрації електронів, хоча кількість переходів для всіх випадків залишається сталою.

2. Рівняння електронейтральності.

Рівняння електронейтральності засноване на тому, що для будь-якого фізично малого об’єму напівпровідника сумарний заряд всіх заряджених частинок рівний нулю. В напівпровідниках  – типу провідності негативний заряд утворюють електрони зони провідності, а позитивний – дірки та позитивно заряджені іони донора. Будемо позначати концентрацію позитивно заряджених донорів через . Тоді рівняння електронейтральності для напівпровідників – типу провідності матиме вигляд:

, (21)

де ; .

Функція Фермі – Дірака визначає розподіл зонних рівноважних носіїв заряду і незастосовна для носіїв заряду, які локалізовані на домішкових центрах. Для зонних носіїв заряду справедливий принцип Паулі: на кожному енергетичному рівні може знаходитись не більше двох електронів з протилежними спінами. Сильне кулонівське відштовхування призводить до того, що принцип Паулі непримінимий для носіїв заряду на домішкових центрах. Ймовірність заповнення таких центрів електронами і дірками визначається наступними співвідношеннями:

– ймовірність заповнення електроном донорного рівня з

енергією (незаряджений донор).

– ймовірність заповнення діркою акцепторного рівня з

енергією (незаряджений акцептор).

– ймовірність заповнення діркою донорного рівня з

енергією (донорний рівень позитивно заряджений).

 – ймовірність заповнення електроном акцепторного рівня

(акцепторний рівень негативно заряджений).

При низьких температурах число теплових переходів дуже мале, тому і величиною в рівнянні (21) можна знехтувати.

Розглянемо спочатку такі температури, при яких донори не повністю іонізовані. Тоді

(22)

, (23)

Позначимо ,

,

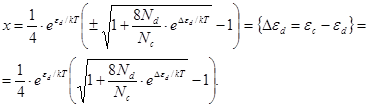
При низьких температурах величина і тоді

,

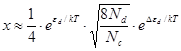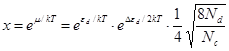
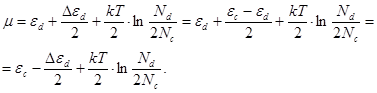(24)

Тоді концентрація електронів в зоні провідності, згідно з (11) та (24),

. (25)

Аналогічно можна отримати вирази для положення рівня Фермі та концентрації дірок в напівпровіднику, який містить мілкі акцепторні центри:

, (26)

. (27)

Співвідношення (25) і (27) в координатах () та () являють собою прямі, тангенс кута нахилу яких чисельно рівний та

відповідно, що дозволяє знайти в напівпровіднику енергію іонізації донорів та акцепторів.

При високих температурах всі донори будуть іонізовані, тобто , і не можна при цьому також знехтувати концентрацію дірок . Тоді

. (28)

Використовуючи закон діючих мас (20),

, (29)

, .

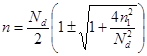Так, як , то від’ємний корінь треба відкинути. Отже,

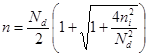. (30)

Вираз для рівня Фермі, згідно з (11) та (30),

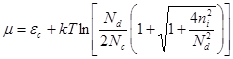. (31)

Розглянемо два випадки в області високих температур.

1. Проміжні високі температури, коли .

Тоді з (30) слідує, що , а .

В цій області температур концентрація електронів не залежить від температури і рівна концентрації донорів. Таку область температур, коли концентрація електронів рівна концентрації домішки і не залежить від температури називають областю виснаження домішки.

2. Дуже високі температури, коли . Тоді, згідно з (30), ,

а .

При таких температурах концентрація електронів і рівень Фермі будуть визначатись як і для власного напівпровідника.

На рис. 5 зображено залежність в широкому інтервалі температур для трьох різних концентрацій домішки.

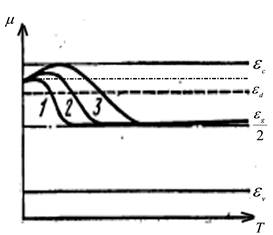
Рис. 5. Залежність рівня Фермі від температури для трьох різних концентрацій донорної домішки:

Із даного рисунка слідує, що при T=0 рівень Фермі в напівпровіднику – типу провідності знаходиться посередині між дном зони провідності та донорним рівнем і при збільшенні температури піднімається вгору до рівня , а потім опускається вниз до середини забороненої зони.

Температурну залежність концентрації носіїв заряду представлено на (рис. 6).

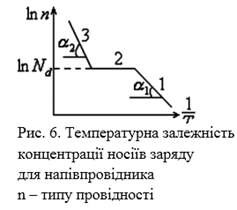
Тут

, .

1 – область домішкової провідності;

2 – область виснаження домішки;

3 – область власної провідності.

За величиною концентрації носіїв заряду в області виснаження домішки можна визначити концентрацію донорів.

5. Концентрація носіїв заряду та рівень Фермі у виродженому напівпровіднику. Критична концентрація домішки

До цього ми розглядали невироджені напівпровідники, для яких розподіл носіїв заряду описується статистикою Максвелла – Больцмана . Для виготовлення багатьох напівпровідникових приладів використовуються напівпро-відникові матеріали з концентрацію домішок , що відповідає виродженому стану. Для прикладу розглянемо напівпровідник типу провідності. Умовою переходу такого напівпровідника у вироджений стан будемо вважати рівність (для типу ). Як відомо, рівень Фермі досягає максимального значення при низьких температурах, коли описується виразом (24): . Знайдемо концентрацію донорів , при якій напівпровідник переходить у вироджений стан . Для цього спочатку знайдемо температуру , при якій функція має максимум:

, , ,

, ,

, (32)

,

, (33)

,

. (34)

Максимальне значення , коли .

Тоді, згідно з співвідношеннями (32) та (33),

. (35)

Знайдемо критичну концентрацію донорів, поклавши

, ,

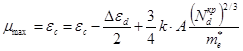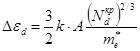. (36)

Із співвідношення (36) слідує, що найбільш вигідним напівпровідниковим матеріалом для створення виродженого стану є напівпровідники з малою енергією іонізації домішок та малою ефективною масою носіїв заряду. У разі цього можна створити вироджений стан при невеликому рівні легування, наприклад, для антимоніда індія (InSb) .

Слід також зауважити, що концентрація домішки, згідно з (36), яка необхідна для виродження є насправді меншою. Це пояснується тим, що при великих концентраціях домішки домішковий рівень розщеплюється і перетворюється в зону. При цьому енергія іонізації домішки із збільшенням її концентрації зменшується. Типова залежність енергії іонізації домішки миш’яку в германії від її концентрації представлена на рис. 7.

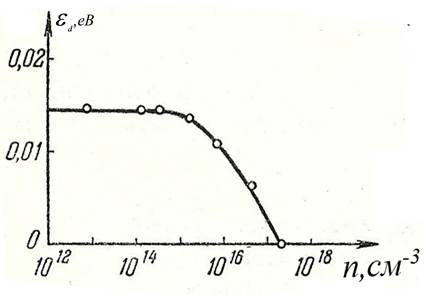
Рис. 7. Залежність енергії іонізації домішки мишʼяку в германії від її концентрації

На рис. 8 представлено температурну залежність концентрації носіїв заряду з різним вмістом домішки

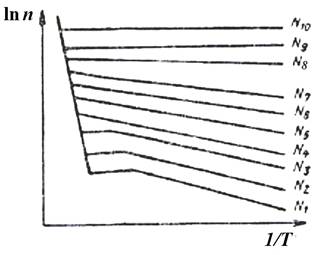
Рис. 8. Температурна залежність концентрації носіїв заряду в напівпровіднику з різним вмістом домішки

Як видно з рис. 8, при деякій концентрації домішки N₄ горизонтальна ділянка області виснаження домішки зникає. Це означає, що збудження електронів з валентної зони почалось раніше, ніж повністю іонізувались домішкові атоми. При концентрації домішки рівній N₈ енергія її іонізації буде рівна нулю, а концентрація носіїв заряду не залежатиме від температури.

Умова є умовою переходу напівпровідника – типу провідності у вироджений стан. Але це не є повністю вироджений напівпровідник, в якому концентрація електронів не залежить від температури (так як і в металі). Дослідження показують, що напівпровідник буде повністю виродженим, якщо , тобто рівень Фермі має знаходитись в зоні провідності на відстанні від її дна більшому, ніж . Для знаходження концентрації електронів та рівня Фермі у виродженому напівпровіднику необхідно використати квантову статистику Фермі – Дірака.

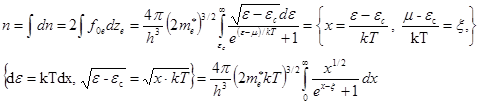
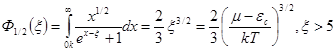
. (37)

Із (37) можна знайти вираз для знаходження рівня Фермі у виродженому напівпровіднику:

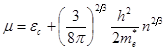. (38)