7.15. Простий алгоритм заповнення із затравкою

Використовуючи стек, можна розробити простий алгоритм заповнення гранично-визначеної області. Стек − це просто масив або інша структура даних, в яку можна послідовно поміщати значення і з якої їх можна послідовно витягувати. Коли нові значення додаються або поміщаються в стек, всі інші значення опускаються вниз на один рівень. Коли значення видаляються або витягуються із стека, інші значення спливають або піднімаються вгору на один рівень. Такий стек називається стеком прямої дії або стеком з дисципліною обслуговування «першим прийшов, останнім обслужений» (FIFO). Простий алгоритм заповнення із затравкою можна представити у наступному вигляді:

Простий алгоритм заповнення із затравкою і стеком

Помістити затравочний піксель в стек

Доки стек непорожній.

Витягти піксель зі стека

Присвоїти пикселю потрібне значення

Для кожного із сусідніх до поточного 4-зв'язого пікселя перевірити: чи є він граничним піксельом або чи не присвоєно вже пікселю потрібне значення. Проігнорувати піксель в будь-якому з цих двох випадків. В іншому випадку помістити піксель в стек.

Алгоритм можна модифікувати для 8-зв'язних областей, якщо переглядати 8-зв'язні пікселі, а не лише 4-зв'язні. Наведемо більш формальний виклад алгоритму, в якому припускається існування затравочного пікселя і гранично-визначеної області

Простий алгоритм заповнення

Затравка (х, у) видає затравочний піксель

Push − процедура, яка поміщає піксель в стек

Pop − процедура, яка витягує піксель зі стека

Піксель (х, у) = затравка (х, у)

ініціалізуємо стек

Push Піксель (х, у)

while (стек не порожній)

витягаємо піксель зі стека

Pop Піксель (х, у)

if Піксель (х, у) <> Нов___ значення then

Піксель (х, у) = Нов___значення

end if

перевіримо, чи потрібно поміщати сусідні пікселі в стек

if (Піксель (х + 1, у) <> Нов___значення and

Піксель (х + 1, у) <> Гран___значення) then

Push Піксель (х + 1, у)

if (Піксель (х, у + 1) <> Нов___значення and

Піксель (х, у + 1) <> Гран___значення) then

Push Піксель (х, у + 1)

if (Піксель (х - 1, у) <> Нов___значення and

Піксель (х - 1, у) <> Гран___значення) then

Push Піксель (х - 1, у)

if Піксель (х, у – 1) <> Нов___значення and

Піксель (х , у- 1) <> Гран___значення) then

Push Піксель (х, у - 1)

end if

end while

В алгоритмі перевіряються і поміщаються в стек 4-зв'язні пікселі, починаючи з правого від поточного пікселя. Напрямок обходу пікселів − проти годинникової стрілки.

Приклад 7.10. Простий алгоритм заповнення із затравкою.

Як приклад застосування алгоритму розглянемо гранично-визначену полігональну область, задану вершинами (1, 0), (7, 0), (8, 1), (8, 4), (6, 6), (1, 6), (0, 5) і (0, 1). Область наведена на рис. 7.32. Затравний піксель − (4, 3). Область заповнюється піксель за піксельом в порядку, зазначеному на рис. 7.32 лінією зі стрілками. Числа, зображені на пікселі, позначають позицію пікселя в стеці, що займається при роботі алгоритму. Для деяких пікселів таких чисел декілька. Це означає, що піксель поміщали в стек більше одного разу. Коли алгоритм доходить до пікселя (5, 5), стек налічує 25 рівнів глибини і містить пікселі (7, 4), (7, 3), (7, 2), (7, 1), (6, 2), ( 6, 3), (5, 5), (6, 4), (5, 5), (4, 4), (3, 3), (3, 4), (3, 5), (2, 4), (2, 3), (2, 2), (2, 2), (3, 2), (5, 1), (3, 2), (5, 2), (3, 3) , (4, 4), (5, 3).

Так як всі пікселі, що оточують (5, 5), містять або граничні, або нові значення кольору, то жоден з них в стек не поміщається. Отже, зі стека витягується піксель (7, 4) і алгоритм продовжує заповнювати колонку (7, 4), (7, 3), (7, 2), (7, 1). При досягненні пікселя (7, 1) перевірка знову показує, що суміжні пікселі або вже заповнені, або є граничними пікселями. Так як в данй момент багатокутник повністю заповнений, то витягання пікселів зі стека до повного його ощищення не викликає появи додаткових пікселів, які слід заповнити. Коли стек стає порожнім, алгоритм завершує роботу.

Багатокутник з прикладу 7.12 є однозв'язною областю, але алгоритм буде правильно заповнювати ті області, що містять порожнини. Це показано в наступному прикладі.

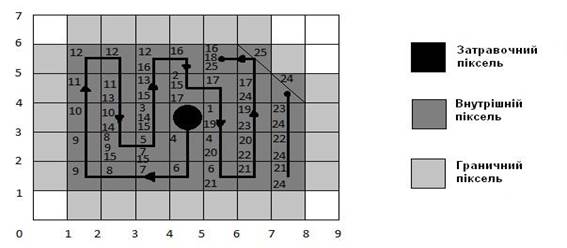
Рис. 7.32. Затравне заповнення за допомогою простого стекового алгоритму

Приклад 7.11. Алгоритм заповнення із затравкою для багатокутника з порожниною.

Як приклад застосування алгоритму розглянемо гранично-визначену область, що містить порожнину. Вона наведена на рис. 7.33. Як і в попередньому прикладі, вершини багатокутника задані пікселями (1, 0), (7, 0), (8, 1), (8, 4), (6, 6), (1, 6), (0 , 5) і (0, 1). Внутрішня порожнина визначається пікселями (3, 2), (5, 2), (5, 3), (3, 3). Затравний піксель − (4, 4). Через порожнини багатокутник заповнюється не в тому порядку, як у прикладі 7.10. Новий порядок заповнення наведений на рис. 7.33 лініями зі стрілками. Як і в попередньому прикладі, числа у квадраті пікселя показують позицію, що займається піксельом в стеці. Коли обробка доходить до пікселя (3, 1), всі суміжні його 4-зв'язні пікселі або вже заповнені, або являються граничними. Тому ні один з пікселів не поміщається в стек. Глибина стека в цей момент дорівнює 15. У стеці знаходяться пікселі (7, 1), (7, 2), (7, 3), (6, 5), (7, 4), (6, 5), (3, 1), (1, 2 ), (1, 3), (1, 4), (2, 5), (3, 5), (4, 5), (5, 4).

Після видалення зі стека пікселя (7, 1) заповнюється колонка (7, 1), (7, 2), (7, 3), (7, 4), при цьому ні один новий піксель в стек не додається. Для пікселя (7, 4) знову всі 4-зв'язні суміжні пікселі або вже заповнені, або є граничними. Звертаючись до стека, алгоритм витягує піксель (6, 5), його заповнення завершує заповнення цього багатокутника. Подальша обробка відбувається без будь-якого затравлення, і коли стек стає порожнім, алгоритм завершує роботу.