7.16. Построковий алгоритм заповнення із затравкою
Як видно з обох
прикладів, стек може стати досить великим. Ще один недолік попереднього
алгоритму − стек найчастіше містить дублюючу або
непотрібну інформацію. В порядковому алгоритмі заповнення із затравкою розмір стека мінімізується за рахунок зберігання
лише одного затравочного пікселя для будь-якого безперервного інтервалу на скануючому рядку. Неперервний інтервал − це група приєднаних один до одного пікселів (обмежена вже заповненими
або граничними пікселями). Для розробки алгоритму використовуємо евристичний
підхід, проте також можливий і теоретичний підхід, що заснований на теорії
графів.
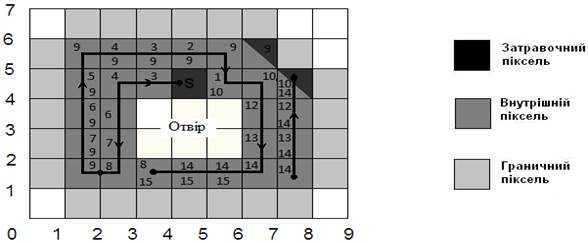
Рис. 7.33. Затравне заповнення області з порожниною за допомогою
простого стекового алгоритму
Даний алгоритм
застосуємо до гранично-визначених областей. Гранично-визначена 4-зв'язна
область може бути як опуклою, так і не опуклою, а також може містити порожнини.
В області,
зовнішньої і прилеглої до нашої гранично-визначеної області, не повинно бути
пікселів з кольором, яким область або багатокутник заповнюється. Схематично
роботу алгоритму можна розбити на чотири етапи.
Порядковий алгоритм
заповнення із затравкою − затравний піксель на інтервалі витягується зі стека, що
містять затравні пікселі.
Інтервал із затравним піксельом заповнюється
вліво і вправо від затравки вздовж скануючого рядка до тих пір, поки не буде знайдена межа.
У змінних Xлів і Хправ
запам'ятовуються крайній лівий і крайній правий піксель інтервалу.
У діапазоні Xлів ≤ х ≤ Хправ.
перевіряються рядки, що розміщуються безпосередньо над і під поточним рядком.
Визначається, чи є на них ще не заповнені пікселі. Якщо пікселі є (тобто, не
всі пікселі граничні або вже занаповнені), то в
зазначеному діапазоні крайній правий піксель в кожному інтервалі відзначається
як затравний і поміщається в стек.
При ініціалізації
алгоритму в стек поміщається єдиний затравний
піксель, робота завершується при очищенні стека. Як наведено на рис. 7.34 і в
прикладі нижче, алгоритм справляється з порожнинами та зубцями на межі. Нижче
наводиться більш докладний опис алгоритму на псевдокоді.
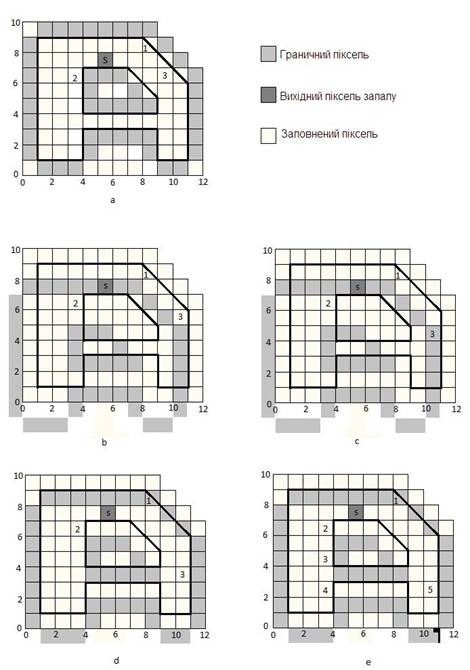
Рис. 7.34.
Порядковий алгоритм заповнення із затравкою для
багатокутника
Построковий алгоритм заповнення із затравкою
Затравка (х, у) видає затравний
піксель
Pop − процедура,
яка витягує піксель зі стека.
Push −
процедура, яка поміщає піксель в стек
Ініціалізуєм стек
Push Затравка (х,
у)
while (стек не порожній)
витягуємо піксель зі стека і
присвоюємо йому нове значення
Pop Піксель (х, у)
Піксель (х, у) = Нов значення
зберігаємо х-координату затравного пікселя
Час___х = х
заповнюємо інтервал праворуч
від затравки
X
= X + 1
while Піксель (х, у) <> Гран___ значення
Піксель
(х, у) = Нов___значення
х
= х + 1
end while
зберігаємо крайній праворуч
піксель
Х-прав
= х - 1
відновлюємо х-координату затравки
х
= Час х
заповнюємо інтервал ліворуч
від затравки
х
= х - 1
While Піксель (х, у) <> Граничні значення
Піксель
(х, у) = Нові значення
X
= X - 1
end while
зберігаємо крайній ліворуч
піксель
Хлів
= х + 1
відновлюємо х-координату затравки
х
= Час х
перевіримо, чи рядок вище не
є ні межею багатокутника, ні вже повністю заповненим; якщо це не так, то знайти
затравку, починаючи з лівого краю підінтервалу
скануючого рядка
х = Хлів
у
= у + 1
while х <Хправ
шукаємо затравку
на рядку вище
Флажок = 0
while (Піксель (х, у) <> Гран___значення
and
Піксель (х, у) <> Нов___значення
and x <Хправ
if Флажок = 0 then Флажок
= 1
X
= X + 1
end while
поміщаємо в стек крайній
праворуч піксель
if Флажок = 1 then
if (x = Хправ and Піксель (х,
у) < > Гран_значення and Піксель (х, у) < > Нов_значення) then
Push Піксель (х, у)
else
Push Піксель (х - 1, у)
end if
Флажок = 0
end if
продовжимо перевірку, якщо
інтервал був перерваний
Хвхід = х
while ((Піксель (х, у) = Гран_значення
or Піксель
(х, у) =
=
Нов значення) and x <Хправ)
X
= X + 1
end while
переконаємось, що координата
пікселя збільшена
If х = Хвхід then х = х + 1
end while
перевіримо, чи рядок нижче
не є ні межею багатокутника, ні вже повністю заповненою
ця частина алгоритму
абсолютно аналогічна перевірці для рядка вище, за винятком того, що замість у = у + 1 потрібно підставити у = у - 1
end while
finish
Тут функція Pop витягує
координати х,у пікселя зі стека, а функція Push поміщає їх
в стек.
Приклад 7.12. Построковий алгоритм заповнення із затравкою.
Розглянемо роботу
алгоритму для гранично-визначеної області наведеної на рис. 7.34. При ініціалізації в стек
поміщається затравний піксель, позначений як затравка (5,7) на рис. 7.34,а. Спочатку в якості затравки інтервалу зі стека витягується цей піксель.
Інтервал заповнюється праворуч і ліворуч від затравки.
Знайдені при цьому кінці інтервал Xправ = 9 та Хлів =
1. Тоді перевіряється строка, що розміщена вище
поточної і виявляється, що вона не гранична і не заповнена. Крайнім правим піксельом в діапазоні 1 ≤ х ≤ 9 виявляється
піксель (8,8), позначений цифрою 1 на рис. 7.34,а. Цей піксель потрапляє у
стек. Тоді аналогічним чином обробляється рядок нижче поточного. У діапазоні Хправ є два підінтервали на цьому
рядку. Для лівого інтервалу в якості затравки
виступає піксель (3,6), що позначений цифрою 2 на рис. 7.34,а, він теж
поміщається в стек. Затравка
для правого підінтервала − піксель (9,6), він потрапляє у стек. Зауважимо, що піксель (9,6) − це не самий крайній правий піксель на інтервалі, однак це самий
крайній правий піксель в діапазоні Хлів ≤ х ≤ Хправ,
тобто, в діапазоні 1 ≤ х ≤ 9. На цьому завершується перший прохід
алгоритму.
Далі зі стека
витягується верхній піксель. Тут заповнюються інтервали, розміщені в правій
частині багатокутника на послідовних скануючих
рядках. Для рядка 3 затравкою служить піксель (10, 3)
(рис. 7.34, d). У результаті заповнення інтервалу праворуч і ліворуч від затравки отримуємо нові межі діапазону: Хлів = 1 та Xправ = 10. Обробляючи рядок вище, отримуємо для лівого підінтервалу затравний піксель
(3,4), який потрапляє у стек. Правий підінтервал до
цього часу вже заповнений. Обробка рядка нижче дає затравку
(3,2) для лівого і (10,2) для правого підінтервалів.
Ці пікселі також помішаються в стек. Саме зараз досягається максимальна глибина
стека для оброблюваного багатокутника.
Тепер залишається
лише один цікавий момент. Після заповнення 4-зв'язних полігональних підобластей з затравними
пікселями 5, 4 і 3 на рис. 7.34,е зі стека витягується піксель, що позначений
цифрою 2. Тут ми виявляємо, що всі пікселі на цьому рядку і на сусідніх рядках
(вище і нижче) вже заповнені. Таким чином, ні один піксель в стек не
поміщається. Зі стека витягується піксель
1 і рядок обробляється, при цьому знову додаткових пікселів не
з'являється. Тепер стек порожній, багатокутник заповнений і робота алгоритму
завершена.
Максимальна глибина
стека в цьому випадку дорівнює п'яти.
Приклади
реалізації
Приклад 7.13. У
площині x-y знайти точки перетину площини з колом.
Вершини:
P0(4:4), P1(4:26), P2(20:26), P3(28:18), P4(21:4), P5(21:8), P6(10:8),
P7(10:4), V0(10:12), V1(10:20), V2(17:20), V3(21:16), V4(21:12)
Uses crt,graph;
Type TPoint = record
X,y:integer;
End;
Const n=7; m=4; s=10; max_elem=32;
Var
grDriver:integer;
grMode:integer;
ErrCode:integer;
P:array[0..n]
of tpoint;
V:array[0..m]
of tpoint;
R:array[0..max_elem-1,0..20]
of integer;
I,j,y,k,bf,im:integer;
Buf:tpoint;
Function det(a11,a12,a21,a22:integer):integer;
Begin
Det2:=a11*a22-a12*a21;
End;
Procedure myline(p1,p2:tpoint;
vara,b,c:integer);
Begin
A:=p2.y-p1.y;
B:=-p2.x+p1.x;
C:=p1.x*(p2.y-p1.y)-p1.y*(p2.x-p1.x);
End;
Function mix(a,b:integer):integer;
Begin if a<=b then min:=a else
min:=b; end;
Function max(a,b:integer):integer;
Begin if a>=b then max:=a else
max:=b; end;
Function intersect (p11,
p12, p21, p22:tpoint; var p:t point):
boolean;
Var d, a1, b1, c1, a2, b2, c2: integer;
Begin
Line(p11, p12, a1,
b1, c1);
Line(p21, p22, a2,
b2, c2);
D:=det2(a1,
b1, a2, b2);
If d=0 then peretun:=false
Else begin
p.x:=round(det2(c1,b1,c2,b2)/d);
p.y:=round(det2(a1,c1,a2,c2)/d);
if p.y in [min(p1.y,p2.y)..max(p1.y,p2.y)] then
peretunsc:true;
end;
end;
function intersectline
(p1,p2:tpoint; y:integer; var p:tpoint):boolean;
var a,b,c,d:integer;
begin
peretunsc:=false;
priama(p1,p2,a,b,c);
if a<>0 then
begin
p.x:=round((c-b*y)/a);
p.y:=round((a*y)/a);
if p.y in [min(p1.y,p2.y)..max(p1.y,p2.y)] then
peretunsc:=true; end;
end;
begin
grDriver:=detect;
InitGraph(grDriver, grMode,’’);
ErrCode:=GraphResult;
If ErrCode=grOk
then
Begin
P[0].x:=4
P[0].y:=4
P[1].x:=4
P[1].y:=26
P[2].x:=20
P[2].y:=26
P[3].x:=28
P[3].y:=18
P[4].x:=21
P[4].y:=4
P[5].x:=21
P[5].y:=18
P[6].x:=10
P[6].y:=8
P[7].x:=10
P[7].y:=4
V[0].x:=10
V[0].y:=12
V[1].x:=10
V[1].y:=20
V[2].x:=17
V[2].y:=20
V[3].x:=21
V[3].y:=16
V[4].x:=21
V[4].y:=12
For i:=0 to max_elem-1 do
For j:=0 to 20 do
r [I,j]:=0;
Moveto(p[n].x*s,p[n].y*s);
For i:=0 to n do
Lineto (p[i].x*s,p[i].y*s);
Moveto(v[m].x*s,v[m].y*s);
For i:=0 to m do
Lineto (v[i].x*s,v[i].y*s);
For y:=0 to max_elem-1 do
For i:=1 to n do
If peretunsc (p[i-1],p[i],y,buf) then begin
Circle(buf.x*s, buf.y*s,s div 2);
K:=r[buf.y,0];inc(k);
R[buf.y,k]:=buf.x;
R[buf.y,0]:=k;
End;
For y:=0 to max_elem-1 do
Begin
K:=r[y,0];
For i:=1 to k do
begin
im:=i;
For j:=i+1 to k-1 do
If r[y,j]<r[y,im]
then im:=j;
Bf:=r[y,im];
R[y,im]:=r[y,i];
R[y,i]:=bf;
End;
End;
For i:=0 to k do
writeln(r[i].x:4,r[i].y:4);
For i:=1 to k do
If (r[i].y<r[i-1].y) or
((r[i].y=r[i-1].y) and (r[i].x<r[i=1].x)) then
Begin
Buf:=r[i-1];
R[i-1]:=r[i];
R[i]:=buf;
End;
Readln;
clrscr;
For i:=0 to k do
writeln (r[i].4:4,r[i].y:4);
Readln;
Circle(r.x*s,r.y*s,s div 2);
closeGraph;
writeln;
for i:=0 to max_elem-1 do begin
for j:=1 to r[I,0] do
write(r[i,j],’’);
writeln;
end;
end
end.
Приклад
7.14. Даний багатокутник, зовнішня частина якого задана точками (4,
5), (4, 26), (20, 26), (28, 18), (21, 4), (21, 8), (10, 8), (10, 4), а
внутрішня точками (10, 12), (10, 20), (17, 20), (21, 16), (21, 12) на растрі
32х32. Напишіть програму, в якій реалізовано стрічковий алгоритм з затравкою для заповнення внутрішньої частини багатокутника.
Затравка – піксель (14, 20)
Uses graph;
Label Label1, Label2, Label3, Label4, Label5,
Label6, Label7, Label8;
Type tpoint=record
X,y:integer;
End;
Var
grDriver:integer;
grMode:integer;
ErrCode:integer;
Right, left, top, down, x1, x2, y1,
y2:integer;
T1, t2: array[1..4] of integer;
Flag:integer;
P, p1, p2,
ppn, pn, pp1, pp2:tpoint;
N, I, h,
s1, s2, m, x, y:integer;
Begin
If x1<left then
t1[4]:=1 else t1[4]:=0;
If x1>right then
t1[3]:=1 else t1[3]:=0;
If y1<down then
t1[2]:=1 else t1[2]:=0;
If x1<top then
t1[1]:=1 else t1[1]:=0;
If x2<left then
t2[4]:=1 else t2[4]:=0;
If x2<right then
t2[3]:=1 else t2[3]:=0;
If y2<down then
t2[2]:=1 else t2[2]:=0;
If y2<top then
t2[1]:=1 else t2[1]:=0;
Flag:=0;
s1:=0;
s2:=0;
Pp1:=p1;
Pp2:=p2;
M:=32000;
For i:=1 to 4 do
begin
s1:=s1+t1[i];
s2:=s2+t2[i];
end;
If (s1=0) and (s2=0) then
goto Label7;
H:=0;
For i:=1 to 4 do
begin
H:=h+trunk((t1[i]+t2[i])/2);
If h<>0 then begin
Flag:=-1;
Goto Label7; end; end;
If s1=0 then begin
N:=1;
Pp1:=p1;
P:=p2;
Goto Label2;
end;
If s2=0 then begin
N:=2;
Pp1:=p2;
P:=p1;
Goto Label2;
end;
N:=0;
Label1: if n<>0 then ppn:=p;
N:=n+1;
If n>2 then goto
Label7;
P:=pn;
Label2: if x2-x1=0 then goto Label4;
M:= round((y2-y1)/(x2-x1));
If left < p.x
then goto label3;
y:=m*(left-p.x)+p.y;
If y>top then
goto Label3;
If y<down then
goto Label3;
p.y:=y;
p.x:=Left;
goto Label1;
Label3: if right>p.x
then goto Label4;
y:= m(right-p.x)+p.y;
If y>top then
goto label4;
If y<down then
goto label4;
p.y:=y;
p.x:=right;
goto Label1;
If m=0 then goto
Label1;
If top>p.y then goto Label5;
X:=trunk(1/m)*(top-p.y)+p.x;
If x<left then
goto Label5;
If x>right then
goto Label5;
p.x:=x;
p.y:=top;
goto label1;
If down < p.y
then goto Label8;
x:=trunc(1/m*(down-p.y)+p.x);
If x<left then
goto Label6;
If x>right then
goto Label6;
p.x:=x;
p.y:=down;
goto label1;
Label6: flag:=-1;
Label7: if flag=-1 then
goto Label 8;
grDriver:=detect;
initGraph(grDriver, grMode,’’);
ErrCode:=Graphresult;
If ErrCode:=grOk
then begin
Line(pp1.x,pp1.y,pp2.x,pp2.y);
End;
Readln;
Label8;
End.