7.14. Алгоритм заповнення із затравкою

У наведених вище алгоритмах заповнення відбувається в порядку сканування. Інший підхід використовується в алгоритмах заповнення із затравкою. В них передбачається, що відомий хоча б один піксель з внутрішньої області багатокутника. Алгоритм намагається знайти і зафарбувати всі інші пікселі, що належать внутрішній області. Області можуть бути або внутрішньо-, або гранично-визначеними. Якщо область відноситься до внутрішньо-визначеної, то всі пікселі, що належать внутрішній частині, мають один і той же колір або інтенсивність, а всі пікселі, які зовнішні по відношенню до області, мають інший колір. Це наведено на рис. 7.28. Якщо область відноситься до гранично-визначеної, то всі пікселі на межі області мають виділене значення або колір, як це наведено на рис. 7.29. Жоден з пікселів з внутрішньої частини такої області не може мати це виділене значення. Тим не менше пікселі, які зовнішні у відношенні до межі, також можуть мати граничне значення. Алгоритми, що заповнюють внутрішньо-визначені області, називаються внутрішньо-заповнюючими, а алгоритми для гранично-визначених областей − гранично-заповнюючими. Далі будуть обговорюватися гранично-заповнюючі алгоритми, однак відповідні внутрішньо-заповнюючі алгоритми можна отримати аналогічним чином.

Внутрішньо- або гранично-заповненні області можуть бути 4- або 8-зв'язними. Якщо область 4-зв'яна, то будь-якого пікселя в області можна досягти за допомогою комбінації рухів лише в 4 напрямках: наліво, направо, вгору, вниз. Для 8-зв'язної області пікселя можна досягти за допомогою комбінації рухів у двох горизонтальних, двох вертикальних і 4 діагональних напрямках.

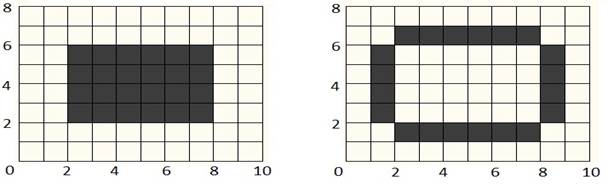
Рис. 7.28. Внутрішньо-визначена область Рис. 7.29. Гранично-визначена область

Алгоритм заповнення 8-зв'язної області заповнить і 4-зв'язну область, проте зворотне невірно. На рис. 7.30 наведені прості приклади 4- і 8-зв'яних внутрішньо-визначених областей. Хоча кожна з підобластей 8-зв'язної області на рис. 7.30,b є 4-зв'язною, для переходу з однієї підобласті в іншу потрібен 8-зв'язний алгоритм. Однак у ситуації, коли потрібно заповнити різними кольорами дві окремі 4-зв'язні підобласті, використання 8-зв'язного алгоритму викличе неправильне заповнення обох областей одним і тим же кольором.

На рис. 7.31 наведена 8-зв'язна область з рис. 7.30, що перевизначена у вигляді гранично-визначеній області. На рис. 7.31 ілюструється той факт, що для 8-зв'язної області, у якої дві підобласті дотикаються кутами, межа 4-зв'язна, а межа 4-зв'язної області 8-зв'язна. Далі мова, в основному, піде про алгоритми для 4-зв'язних областей, проте їх можна легко переробити для 8-зв'язкних областей, якщо заповнення проводити не в 4, а в 8 напрямах.

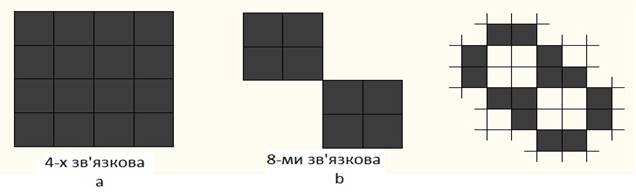
Рис. 7.30. 4 - і 8-зв'язні внутрішньо-визначені області

Рис. 7.31. - і 8-зв'язні гранично-визначені області