Практична робота №2.

Обробка результатів ПРЯМИХ багатократних вимірювань.

 

ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ

 

Похибкою результату вимірювання (або похибкою вимірювання) називається відхилення результату вимірювання від дійсного значення вимірюваної величини.

Всі похибки  вимірювань містять в собі систематичну і випадкову складові, що називаються також систематичною і випадковою похибками .

Систематичними називають похибки, які залишаються постійними або закономірно змінюються при повторних вимірюваннях однієї і тієї ж величини.

Випадковими називаються похибки, що змінюються випадковим чином при повторних вимірюваннях тієї ж величини.

На відміну від систематичних, випадкові похибки не можна заздалегідь виявити і усунути. Вони можуть бути зменшені при багатократних спостереженнях однієї і тієї ж величини, фільтрацією похибок і ін. При цьому необхідно на основі певного ряду значень отримати найкраще наближення вимірюваної величини до її істинного значення.

При вимірюванні ці похибки виявляються спільно, внаслідок чого сукупність результатів вимірювання утворює нестаціонарний, випадковий процес.

Для характеристики випадкового процесу визначають інтегральну і диференційну функції розподілу імовірності випадкової величини.

Інтегральна функція розподілу показує імовірність того, що випадкова величина Х знаходиться в інтервалі від - ∞ до деякого значення, меншого х1, при цьому функція є не спадаюча і F(-∞)=0, а F(+∞)=l.

 

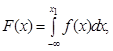                                               (1)

Диференційна функція (густина імовірності) показує імовірність того, що випадкова величина Х набуде значення в інтервалі між x1 і x2, і рівна:

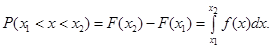                     (2)

 

У практиці електровимірювань  найчастіше мають справу з нормальним законом розподілу. Випадкова величина х розподілена нормально (за законом Гаусса), якщо її густина імовірності має вигляд:

 

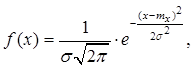                                  (3)

 

де σx – середнє квадратичне відхилення (CКВ), mx – математичне очікування випадкової величини. Функція показує розсіювання результатів навколо деякого середнього значення, і повністю характеризується середнім квадратичним відхиленням (рис. 2.2.б). Чим менше значення СКВ, тим частіше зустрічаються малі випадкові похибки, тобто тим точніше виконані вимірювання.

   

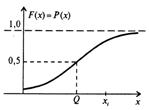
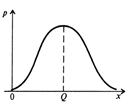
Рис 2.1. Інтегральна  і диференційна функції нормального розподілу імовірності результатів вимірювання.

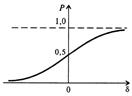
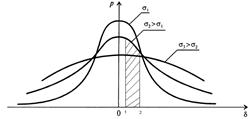
Рис 2.2. Інтегральна  і диференційна функції нормального розподілу імовірності похибок вимірювання.

 

Імовірність появи випадкової величини в інтервалі  визначається площею заштрихованої ділянки (рис 2.б) і визначається як визначений інтеграл від функції (3) в межах (х1, х2). Інтеграл не обчислюється в елементарних функціях, його обчислюють за допомогою таблиць. Для спрощення запису здійснюють заміну змінних:

 

     ,  тоді .                             (4)

Тоді імовірність попадання  результатів вимірювання (або їх похибок) в інтервал  обчислюється  за відомими значеннями t1 i t2 через табличні значення Ф1 і Ф2  (таблиця 2.):

 

.                                         (5)

 

Способи знаходження оцінок ряду спостережень і показники їх якості залежать від законів розподілу. Для нормального розподілу, як і для всіх симетричних розподілів, як оцінку математичного очікування ряду n спостережень приймають середнє арифметичне ряду спостережень:

 

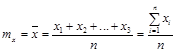     .                                        (6)

 

Величина відхилення результату одиничного вимірювання від середнього значення  є випадковою похибкою і може бути додатною або від’ємною. Якщо систематична похибка  відсутня, то за результат вимірювання беруть математичне очікування випадкової величини:

 

 = ХВ .                                                           (7)

 

Оцінка відхилення результату одного спостереження  від дійсного значення називається дисперсією і обчислюється за формулою:

 

, де                             (8)

 

Тоді середнє квадратичне відхилення однократного вимірювання:

 

     .                                              (9)

 

Середнє арифметичне значення теж залежить від числа спостережень і є випадковою величиною, яка володіє деякою дисперсією відносно дійсного значення величини Хд. Тоді оцінкою середнього квадратичного для середнього арифметичного ряду спостережень відносно дійсного значення (тобто відхилення  при повторних вимірюваннях) є:

 

     ,                                   (11)

 

S – середнє квадратичне відхилення результату вимірювань.

Отже, збільшення кількості вимірювань n веде до зменшення СКВ результату вимірювань.

Оцінки  і  є так званими точковими оцінками вимірюваної величини. Вони вказують інтервал значень вимірюваної величини, усередині якого знаходиться дійсне значення: . 

На відміну від точкової при інтервальній оцінці визначається довірчий інтервал εр, в якому з довірчою імовірністю Р знаходиться дійсне значення Хд:

.                                               (12)

При заданій імовірності Р і обчисленому  значення  визначається законом розподілу. В випадку нормального розподілу і числа вимірювань  n>20 вибирається по таблиці функцій Лапласа. Якщо число вимірювань  n<20, то довірчий інтервал випадкової величини визначається по формулі Стьюдента:

 

,

                                             (13)

де  – коефіцієнт розподілу Стьюдента, який залежить від заданої імовірності Р і числа вимірювань n (таблиця 1).

Таким чином при інтервальній оцінці результат вимірювання записується у вигляді , при Р = ..%. Як правило, приймають Р=0,95. Якщо ж вимірювання не можна повторити, то приймають Р=0,99, а в особливо відповідальних випадках ще вище.

Таблиця 1.

Таблиця коефіцієнтів Стьюдента .

n \ P

0,5

0,6

0,7

0,8

0,9

0,95

0,98

0,99

0,999

2

1,00

1,38

2,0

3,1

6,3

12,7

31,8

63,7

636,6

3

0,82

1,06

1,3

1,9

2,9

4,3

7,0

9,9

31,6

4

0,77

0,98

1,3

1,6

2,4

3,2

4,5

5,8

12,9

5

0,74

0,94

1,2

1,5

2,1

2,8

3,7

4,6

8,6

6

0,73

0,92

1,2

1,5

2,0

2,6

3,4

4,0

6,9

7

0,72

0,90

1,1

1,4

1,9

2,4

3,1

3,7

6,0

8

0,71

0,90

1,1

1,4

1,9

2,4

3,0

3,5

5,4

9

0,71

0,90

1,1

1,4

1,9

2,3

2,9

3,4

5,0

10

0,70

0,88

1,1

1,4

1,8

2,3

2,8

3,3

4,8

20

0,69

0,86

1,1

1,3

1,7

2,1

2,5

2,9

3,9

40

0,68

0,85

1,1

1,3

1,7

2,0

2,4

2,7

3,6

∞

0,67

0,84

1,0

1,3

1,6

2,0

2,3

2,6

3,3

 

Таблиця 2.

 

Інтегральна функція нормального розподілу

 

t

Ф(x)

t

Ф(x)

t

Ф(x)

t

Ф(x)

-3,5

0,00023

-1,7

0,0446

+0,0

0,5000

+1,8

0,9641

-3,4

0,00034

-1,6

0,0548

+0,1

0,5398

+1,9

0,9713

-3,3

0,00048

-1,5

0,0558

+0,2

0,5793

+2,0

0,9773

-3,2

0,00069

-1,4

0,0808

+0,3

0,6179

+2,1

0,9821

-3,1

0,00097

-1,3

0,0968

+0,4

0,6554

+2,2

0,9861

-3,0

0,00135

-1,2

0,1151

+0,5

0,6915

+2,3

0,9893

-2,9

0,0019

-1,1

0,1357

+0,6

0,7157

+2,4

0,9918

-2,8

0,0026

-1,0

0,1587

+0,7

0,7580

+2,5

0,9938

-2,7

0,0035

-0,9

0,1841

+0,8

0,7881

+2,6

0,9953

-2,6

0,0047

-0,8

0,2119

+0,9

0,8159

+2,7

0,9965

-2,5

0,0062

-0,7

0,2420

+1,0

0,8413

+2,8

0,9974

-2,4

0,0082

-0,6

0,2743

+1,1

0,8643

+2,9

0,9981

-2,3

0,0107

-0,5

0,3085

+1,2

0,8849

+3,0

0,99865

-2,2

0,0139

-0,4

0,3440

+1,3

0,9032

+3,1

0,99903

-2,1

0,0179

-0,3

0,3821

+1,4

0,9192

+3,2

0,99931

-2,0

0,0228

-0,2

0,4207

+1,5

0,9332

+3,3

0,99952

-1,9

0,0287

-0,1

0,4602

+1,6

0,9452

+3,4

0,99966

-1,8

0,0359

-0,0

0,5000

+1,7

0,9554

+3,5

0,99977

 

Виключення грубих похибок

В деяких випадках виявляється, що результат одного вимірювання різко відрізняється від результатів інших вимірювань, виконаних за тих же контрольованих умов. В цьому випадку говорять про грубу похибку (промах). Причиною можуть стати помилка оператора, поява значної короткочасної перешкоди, поштовх, порушення електричного контакту і так далі. Такий результат, що містить грубу похибку необхідно виявити, виключити і не враховувати при подальшій статистичній обробці результатів вимірювань.

Згідно формули , для довірчого інтервалу , довірча імовірність рівна 0,9973. Тобто імовірність появи похибки, більшої за 3σ рівна 1-0,9973=0,0027≈1/370. Така довірча імовірність означає, що з 370 випадкових похибок тільки одна по абсолютному значенню буде більша за 3σ. Тому 3σ вважається максимально можливою випадковою похибкою, похибки більше 3σ вважаються грубими і при обробці результатів вимірювань не враховуються.

 

Правила додавання похибок прямих спостережень

Випадкова похибка вимірювального пристрою , що складається з m блоків з випадковими похибками кожного блоку, знаходиться шляхом геометричного додавання:

 

                                                        (14)

Аналогічно визначається відносна і граничні похибки, а також середньоквадратичне відхилення. Систематичні похибки  додаються з врахуванням їх знаків, сумарна похибка  є модулем отриманої суми:

 

.                                                  (15)

При наявності і випадкових і систематичних похибок загальна похибка  приймається рівною їх геометричній сумі:

 

 .                                              (16)

 

МЕТОДИКА РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ

 

Приклад 2.1. Проведено 10 вимірювань фізичної величини Хі, результати показані в таблиці:

 

1

2

3

4

5

6

7

8

9

10

Хі

20,5

20,7

18,6

19,4

20,2

21,1

20,4

21,1

20,2

22,3

Визначити:

-    математичне очікування значення фізичної величини;

-    оцінку СКВ результату вимірювання та

-    інтервал дійсних значень вимірюваної величини;

-    оцінку дійсного значення величини з довірчою імовірністю Р=0,6%, Р=0,99%;

-    такі значення фізичної величини, що означали б появу грубої похибки.

 

Розв’язання

Математичне очікування вимірюваної величини:

 

Середнє квадратичне відхилення результату вимірювання:

 

 

Похибки вимірювання відповідно : 

 

 

1

2

3

4

5

6

7

8

9

10

Хі

20,5

20,7

20,6

19,4

20,2

21,1

20,4

21,1

20,2

22,3

-0,15

0,05

-0,05

-1,25

-0,45

0,45

-0,25

0,45

-0,45

1,65

Виключимо можливість появи грубої похибки: .

Вимірювання № 4 і №10 включають грубу похибку, тому їх потрібно виключити з розрахунку. Перерахуємо значення  і :

 

; .

 

Тоді дійсне значення вимірюваної величини:

 

 

Оцінка дійсних значень вимірюваної величини в довірчому інтервалі:

з імовірністю Р=0,6%:

 

, ;

 

з імовірністю Р=0,99%:

 

, .

 

 

ЗАВДАННЯ ДЛЯ САМОСТІЙНОГО ОПРАЦЮВАННЯ

 

1. Випадкові похибки ряду вимірювань підлягають нормальному закону розподілу:  = 0,5; -1,7; 0,7; -1,4; -0,6; 0,2; 1,1; 0,4; 1,1; 0,2; 2,3. Визначити імовірність того, що величина похибки не перевищує  ±2.

2. Відомий результат вимірювання  при кількості вимірювань n=20, імовірності Р=0,98% і нормальних умовах. Визначити середньоквадратичне відхилення результату вимірювання.

3.       Чи входить результат вимірювання 0,16 мВ до ряду з 14 спостережень з імовірністю 0,95: -0,14; -0,12; -0,1; -0,08; -0,06; -0,04; -0,02; 0,00; 0,02; 0,04; 0,06; 0,08; 0,1; 0,12мВ?

4.       Результат вимірювання напруги в нормальних умовах рівний 225,3±1,5мВ, довірча імовірність 0,95, число спостережень n=19. Визначити середньоквадратичне відхилення результату вимірювання.

5.       При вимірюванні струму в нормальних умовах проведений ряд спостережень в мА: 10,07; 10,08; 10,10; 10,12; 10,15; 10,16; 10,17; 10,20; 10,40. Перевірити чи результат 10,40 містить грубу похибку.

6.       При вимірюванні опору прилад показав: 47,4; 48; 48,1;  48,6; 49,2; 49,8; 50,0; 50,2; 50,4; 50,6; 50,8; 51,0; 52 Ом. Визначити імовірність попадання величини опору в інтервал 49..51 Ом.

7.       При вимірюванні фізичної величини в нормальних умовах виконано 4 спостереження: 2,57; 2,59; 2,58; 2,60. Визначити таке найближче значення величини, яке означало б появу грубої похибки для даного ряду .

8.       При вимірювання струму амперметром класу точності 0,5, з  кінцевим значенням шкали 300А були отримані такі результати, А: 152,5; 153,8; 153,0; 152,3; 152,8; 152,1; 153,2. Записати результат вимірювання з довірчою імовірністю 0,997.

9.       При повірці амперметра класу точності 1,5 з діапазоном вимірювань 2,5А зразковим приладом в точці шкали 1А отримали такі покази: 1,05; 0,95; 1,1; 1,08; 1,05 А. Чи відповідає похибка приладу його класу точності з імовірністю 0,997.

10.   Амперметром класу точності 0,5 з діапазоном вимірювань (0…1)А, зі шкалою на 100 поділок і вхідним опором 0,1 Ом кілька разів вимірюється струм джерела, що має вихідний опір 10 Ом. Відлік по шкалі приладу становить 75; 75,5; 73; 76  поділок. Записати результат вимірювання.

 

ПИТАННЯ ДЛЯ САМОПЕРЕВІРКИ

 

1.   Що таке систематична і випадкова похибки. Які є види запису цих похибок?

2.   Що характеризує математичне очікування випадкової величини?

3.   Як розрахувати середньоквадратичне відхилення ряду вимірювань? Чим від нього відрізняється СКВ результату вимірювання?

4.   Як знайти імовірність попадання випадкової величини в певний інтервал?

5.   Чим відрізняються точкова і інтервальна оцінки дійсного значення величини?

6.   Що таке довірчий інтервал?

7.   Як виявити появу грубої похибки вимірювання?

8.   Як записується результат вимірювання, якщо ряд виміряних величин містить грубу похибку?

9.   Як записується результат вимірювання, що містить і систематичну і випадкову складові похибки?