Коливання та хвилі.

Приклади розв’язування задач

Задача 1. Камертон коливається з частотою 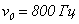 і амплітудою 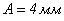. Знайти максимальне прискорення його гілки, що

коливається.

Розв'язання

Рівняння руху гілки камертона має вигляд (у системі СІ):       (1)

Початкова фаза нам не відома, але її значення може бути довільним. За формулою для прискорення:  

.                    (2)

 

Максимальне значення прискорення відповідає тим моментам часу, коли значення синуса, що входить до формули (2), дорівнює

+1 або -1, оскільки істотним є абсолютне значення прискорення. При цьому за абсолютною величиною

.

Задача 2. За час  амплітуда коливань маятника зменшилась у три рази. Визначити коефіцієнт згасання .

Залежність амплітуди згасаючих коливань від часу подається співвідношенням: . 

  

Розв'язання    

 

Відношення амплітуд через проміжок часу : .

 

Коефіцієнт  знайдемо, прологарифмувавши останню рівність: ;   .

Обчислення дають значення  .

Задача 3. Поперечна хвиля поширюється вздовж пружного шнура зі швидкістю . Період коливань точок шнура , амплітуда . Визначити а) довжину хвилі ;     б) фазу коливань, зміщення і швидкість точки середовища, яка знаходиться на відстані  від джерела хвиль в момент часу ; в) різницю фаз коливань двох точок, які лежать на промені і віддалені від джерела хвиль на  і .

Розв'язання

Довжина хвилі дорівнює відстані, яку хвиля проходить за один період, і може бути знайдена зі співвідношення .

Підставивши значення величин  і  одержимо .

Запишемо рівняння хвилі: ,      

де  - зміщення точки, що коливається,  - відстань точки від джерела хвиль,  - швидкість поширення хвиль.

Фаза коливань точки з координатою  в момент часу  визначається виразом, який стоїть під знаком косинуса:

, або ,

 

де враховано, що .

 

Провівши обчислення за останньою формулою, одержимо:

 

, або .

 

Зміщення визначимо, підставивши у рівняння плоскої хвилі значення амплітуди  і фази:

.

Швидкість точки знаходимо, взявши першу похідну від зміщення по часу:

.

 

Підставивши значення величин  і провівши обчислення, одержимо:

Різниця фаз коливань двох точок хвилі зв'язана з відстанню  між цими точками співвідношенням:

.

 

Підставивши значення величин ,  і  та обчисливши, одержимо:

, або .