Т.3 Рівняння Шредінгера

§1. Загальне рівняння Шредінгера (1926 р.)

В нерелятивістській квантовій механіці існує рівняння яке, як і другий закон Ньютона для класичної механіки є основоположним і не виводиться, а постулюється. Таким є рівняння Шредінгера.

•      Рівняння Шредінгера – це основне рівняння квантової механіки.

•      Рівняння Шредінгера дозволяє визначити хвильові функції частинок, які рухаються в силових полях.

•      Рівняння Шредінгера є постулатом, справедливість якого підтверджується тим, що всі наслідки, які випливають з нього добре узгоджуються з експериментальними результатами.

Загальне рівняння Шредінгера має вигляд:

§2. Стаціонарне і часове рівняння Шредінгера

Для задач, в яких потенціальна енергія не залежить від часу:

,

наприклад рух електрона в атомі, необхідно знати стаціонарні (які не містять часової залежності) розв’язки рівняння Шредінгера.

Щоб знайти стаціонарне рівняння Шредінгера представимо псі-функцію частинки у вигляді добутку відокремлених змінних:

^.

Тут:

Підставимо таку псі-функцію у загальне рівняння Шредінгера:

^.

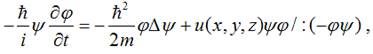
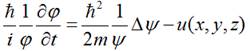Оскільки, ліва частина даного виразу залежить лише від часу, а права – лише від координат, то вираз перетворюється у рівність, якщо обидві частини його рівні тій самій постійній величині (-W):

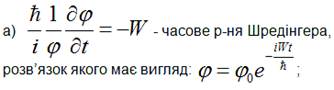
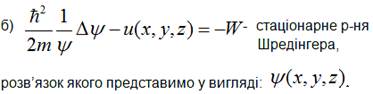
Перепишемо стаціонарне рівняння у стандартному вигляді:

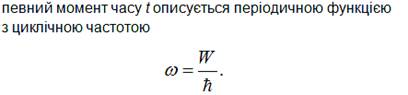
§3. Розв’язок загального рівняння Шредінгера для вільної частинки

1. Для вільної частинки потенціальна енергія рівна нулю:

2. Повна енергія частинки рівна її кінетичній енергії:

.

3. Направимо вісь Ох вздовж вектора швидкості розглядуваної частинки, тоді стаціонарне рівняння Шредінгера набере вигляду:

4. Розв’язком такого диференціального рівняння є функція:

5. Враховуючи, що розв’язком загального рівняння Шредінгера є вираз:

^,

підставивши вираз для в останню формулу, одержимо розв’язок загального рівняння Шредінгера для вільної частинки:

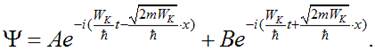
Висновки з розв’язку.

1. Плоска хвиля у комплексному представленні має вигляд:

,

тому видно, що розв’язок для є суперпозицією двох плоских хвиль з однаковими частотами:

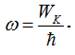
2. Одна з хвиль, з амплітудою А, поширюється в напрямі осі Ох (бо хвильове число – від’ємне), друга – з амплітудою В, поширюється в протилежному напрямі (хвильове число – додатне).

3. Хвильове число для вільної частинки рівне:

4. Враховуючи, що

,

вираз для k набере вигляду:

5. Співпадіння виразу “ k ” для вільної частинки і плоскої хвилі ще раз доводить, що у квантовій механіці вільній частинці відповідає плоска хвиля де Бройля.

§4. Висновки із стаціонарного рівняння Шредінгера для частинки в потенціальній ямі

ІV. І. Умови потенціальної ями

Потенціальна яма - вид потенціального поля, у якому потенціальна енергія частинки має наступні значення (див. рис.3. 1):

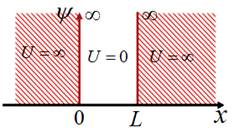
Рис. 3. 1

Зауваження. частинка набути не може, отже, поза межами ями частинка не існує.

Застосуємо до частинки в потенціальній ямі (електрона в бруску провідника) стаціонарне рівняння Шредінгера:

Для одномірного випадку в межах ями () дане рівняння запишеться:

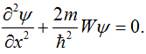
Відомо, що:

Тоді рівняння набере вигляду:

Розв’язком такого диференціального рівняння є вираз:

ІV. ІІ. Квантування хвильового числа хвиль де Бройля

Розглянемо розв’язок диференціального рівняння для частинки в потенціальній ямі:

В точці

^,

бо поза ямою частинка не існує.

тому наш розв’язок матиме вигляд:

Для того, щоб дана рівність виконувалась треба, щоб

В точці

^,

бо поза ямою частинка не існує.

У випадку, коли , розв’язок набере вигляду:

Якщо вважати, що , тоді:

тобто в потенціальній ямі k повинно набувати лише такі дискретні значення, які задовольняють умову:

Виходячи з попереднього:

Висновок. Хвильове число частинки в потенціальній ямі є квантованим.

ІV. ІІІ. Квантування довжини хвилі де Бройля для частинки в потенціальній ямі

Відомо, що:

З іншого боку хвильове число визначається:

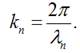
Прирівнявши праві частини даних виразів, одержимо:

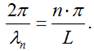
Звідки:

Висновок. Довжина хвилі де Бройля для даної частинки повинна бути такою, щоб в ямі шириною L вкладалось ціле число півхвиль де Бройля, що їй відповідають.

ІV.ІV. Квантування енергії частинки в потенціальній ямі

З умови потенціальної ями відомо, що

З цього рівняння знайдемо значення енергії частинки:

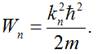
Підставивши значення хвильового числа у таку формулу, одержимо:

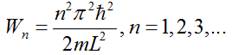
Висновок. Енергія частинки в потенціальній ямі може мати лише дискретні значення, тобто є квантованою (n-головне квантове число).

ІV. V. Власні функції для частинки в потенціальній ямі

Для частинки в потенціальній ямі:

У випадку, коли , хвильова функція запишеться:

де

Щоб знайти коефіцієнт В застосуємо умову нормування функції, яка в нашому випадку має вигляд:

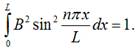
Існує табличний інтеграл:

Тоді з останніх двох формул:

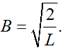
Отже, власні функції частинки в потенціальній ямі матимуть вигляд:

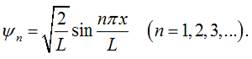
§5. Тунельний ефект

V.І. Сходиноподібний потенціальний бар’єр.

Нехай частинка рухається вздовж осі Оx і зустрічає потенціальний бар’єр, зображений на рисунку 3. 2.

Рис. 3. 2

Потенціальна енергія частинки при x<0 U=0, а при x>0 U=U₀.

1. Поведінка класичної частинки.

а) У випадку, коли повна енергія частинки E₁<U₀, частинка відіб’ється від бар’єру та полетить у зворотній бік з тією самою енергією, яку вона мала спочатку.

б) Якщо повна енергія частинки E₂>U_0, частинка пройде над бар’єром, втративши частину своєї швидкості і буде рухатися далі без перешкод.

2. Поведінка квантової частинки.

У випадку E₁<U₀, частинка проникне в бар’єр на певну глибину, причому її хвильова функція буде зменшуватися за експонентою і тільки потім поверне назад.

Глибиною проникнення називається відстань, на якій ймовірність виявити частинку зменшується в e разів.

Приклад. Для електронів у металі , тобто вільні електрони вилітають за межі металу на відстань такого порядку, після чого повертаються назад. Отже, металеве тіло виявляється оточене з усіх боків хмарою електронів.

V.ІІ. П – подібний потенціальний бар’єр.

Розглянемо випадок потенціального бар’єру конечної ширини d, який зображено на рисунку 3. 3.

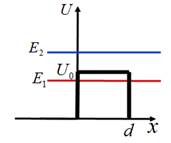
Рис. 3. 3

1. Класична частинка відбивається так само, як від нескінченного бар’єру. Ймовірність пройти крізь бар’єр у класичної частинки дорівнює нулю.

2.Квантова частинка може опинитися за бар’єром навіть при Е₁<U₀ та відбитися від нього навіть при Е₂>U₀.

Ймовірність того, що частинка опиниться за бар’єром, визначається коефіцієнтом прозорості:

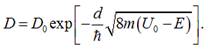
Ймовірність того, що квантова частинка відіб’ється від бар’єру і полетить у зворотному напрямку визначається коефіцієнтом відбивання: