Т.2 Елементи квантової механіки
§1. Корпускулярно – хвильовий дуалізм речовини і поля. Гіпотеза де Бройля
І.І. У 1924 р. де Бройль висунув
гіпотезу про універсальність
корпускулярно-хвильового дуалізму: кожному мікрооб’єкту з одного боку притаманні
корпускулярні характеристики (енергія і імпульс), а з іншого – хвильові
характеристики (частота і довжина хвилі).
Припустивши, що співвідношення між імпульсом фотона і довжиною
його хвилі має універсальний характер для довільного матеріального об’єкта, де
Бройль довів наступну формулу:
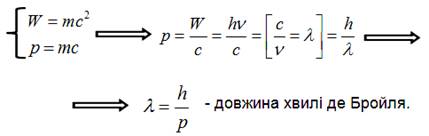
Висновок.
Кожному матеріальному об’єкту, що має імпульс, відповідає плоска
хвиля з певною довжиною хвилі.
І.ІІ. Для частинки, що має масу і швидкість
набагато меншу за швидкість світла:
1)
імпульс частинки: ![]()
а значить
довжина хвилі де Бройля визначатиметься:
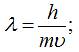
2) якщо
відома кінетична енергія частинки, тоді імпульс частинки:
![]()
а
значить:
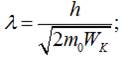
3) для
електрона, прискореного різницею потенціалів:
![]()
а
значить:
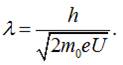
І.ІІІ. Якщо швидкість частинки співмірна з швидкістю світла:
1)
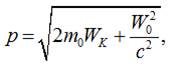
де ![]()
Тоді:
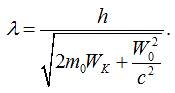
2) Якщо
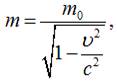
враховуючи,
що імпульс:
![]()
одержимо:
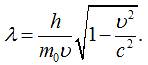
§2.
Дослід Девіссона і Джермера
на підтвердження корпускулярно - хвильового дуалізму (1927р.)
ІІ. І. Схема експерименту
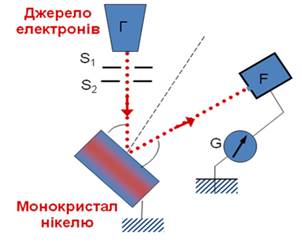
Рис. 2. 1
Г –
електронна гармата; S – діафрагма для утворення вузького пучка електронів;
F –
циліндр Фарадея; G – гальванометр.
ІІ. ІІ. Результати експерименту
Залежність інтенсивності розсіяних електронів, падаючих на
кристал під кутом 650 від їх кінетичної енергії представлено на рис.
2.2.
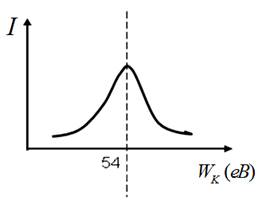
Рис. 2. 2
Якщо за формулою
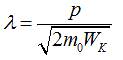
визначити
довжину хвилі де Бройля і підставити її
у формулу Вульфа-Брегів щодо дифракції
електромагнітних хвиль на просторовій ґратці:
![]()
то
обчислений напрям на перший дифракційний максимум дасть кут 650.
ІІ.ІІІ. Висновок
В
експериментах з дифракції на просторовій ґратці електрони:
- з одного
боку, ведуть себе як частинки (корпускули), коли енергія надається їм різницею
потенціалів у електронній гарматі;
- з іншого боку, електрони ведуть себе як хвилі,
коли беруть участь у дифракції за законом Вульфа-Брегів.
Отже,
двоїста корпускулярно-хвильова природа частинок, як передбачав де Бройль,
була підтверджена експериментально.
§3. Властивості хвиль де Бройля
ІІІ. І. Чому хвильові процеси (дифракція) не
спостерігаються у кулі, що вилетіла з гвинтівки?
За
формулою для довжини хвилі де Бройля
![]()
Підставимо
значення фізичних величин:
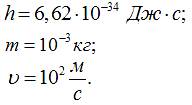
Розрахунки дають довжину хвилі:
![]()
Проте, щоб спостерігати дифракційну картину,
необхідна дифракційна ґратка з періодом співмірним з
довжиною хвилі. Враховуючи, що найменший
розмір доступний людині сьогодні є розмір
атома ( 10-10 м ),
зрозуміло, що спостерігати таку
дифракцію немає можливості.
ІІІ.ІІ. Фазова швидкість хвиль де Бройля
Швидкість руху хвильової поверхні
(поверхні сталої фази) для синусоїдальної хвилі називається фазовою швидкістю.
Враховуючи, що фазова швидкість
довільної хвилі, в тому числі і хвилі де Бройля, визначається виразом:
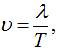
знаючи що:
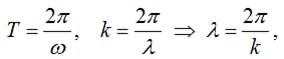
а значить:
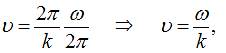
одержимо:
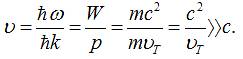
Висновок.
Вважаючи, що не існує об’єктів із
швидкістю більшою за швидкість світла, хвилі де Бройля не мають
природного аналога.
ІІІ.ІІІ. Групова швидкість хвиль де Бройля
Визначимо групову швидкість хвиль де Бройля, як
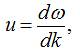
де ![]() - інтервал циклічних частот хвиль
групи;
- інтервал циклічних частот хвиль
групи;
![]() - інтервал хвильових чисел хвиль групи.
- інтервал хвильових чисел хвиль групи.
Тому
групову швидкість представимо:
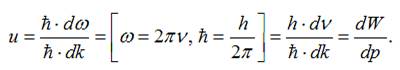
Враховуючи, що:
![]()
а також те, що:
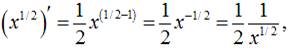
одержимо:
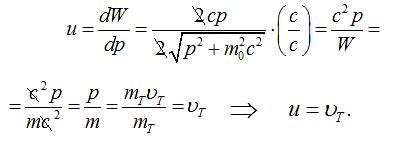
Висновок. Групова швидкість хвиль де Бройля рівна
швидкості відповідного їй тіла.
ІІІ.ІV. Імпульс хвиль де Бройля
З формули
для довжини хвилі де Бройля:
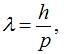
знайдемо імпульс хвиль де Бройля:
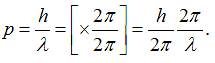
Враховуючи, що:
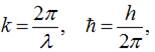
вираз для імпульсу хвиль де
Бройля набере вигляду:
![]()
або у
векторному вигляді:
![]()
Висновок. Імпульс
хвилі де Бройля співпадає за величиною і напрямом з імпульсом плоскої
хвилі.
§4. Хвильова функція і її
статистичний зміст
1. З точки зору хвильової теорії, максимуми картини дифракції
електронів у досліді Девіссона і Джермера
відповідають найбільшій інтенсивності хвиль де Бройля.
2. Але процес попадання електронів у різні місця на фотоплівці
не є індивідуальним.
3. Принципово неможливо передбачити, куди саме попаде черговий
електрон після розсіювання. Тому існує лише певна ймовірність попаданняелектрона
у те чи інше місце.
4. Таким чином, опис стану мікрооб'єкта та його поведінку можна
подати лише виходячи з поняття ймовірності.
5. Тому у квантовій механіці для
характеристики станів мікрооб'єктів у мікросвіті вводять поняття хвильової функції (псі - функції):
![]()
Макс Борн у 1926р дав фізичну
інтерпретацію хвильової псі - функції: квадрат модуля хвильової функції визначає
ймовірність, з якою частинка може бути виявлена в одиничному об’ємі простору,
тобто є густиною ймовірності:
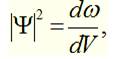
де ![]() ,
,
є
ймовірність появи частинки в елементі простору ![]() .
.
Ймовірність
знайти частинку у певному об’ємі простору ![]() визначається:
визначається:
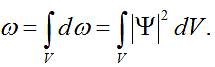
Висновок.
З фізичного змісту хвильової функції випливає, що вона має
статистичний характер:
1) не
дозволяє встановити траєкторію та координати частинки у просторі;
2)дає
можливість лише передбачити ймовірність знаходження частинки в різних точках
простору
Для об’єктивної характеристики стану мікрочастинки хвильова функція цієї частинки повинна задовольняти
ряд умов:
1) псі -
функція повинна бути скінченна;
2)
псі-функція повинна бути однозначна;
3)
псі-функція повинна бути неперервна;
4)
часткові похідні по часу і координатах псі-функції мають бути неперервними;
5)
псі-функція повинна виконувати умову нормування на одиницю:
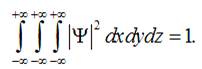
Умова нормування:ймовірність знайти частинку у всьому фізичному просторі є
достовірною подією з ймовірністю рівною одиниці.
§5. Співвідношення невизначеності Гейзенберга
У 1927 році німецький фізик В. Гейзенберг
проаналізував, як впливають хвильові властивості мікрочастинок на їх поведінку.
Результати досліджень привели до висновку:
об'єкт
мікросвіту неможливо одночасно, з наперед заданою точністю, характеризувати і
координатою, і імпульсом.
V.І. Співвідношення невизначеності для координати
та імпульсу
Мікрочастинка (мікрооб'єкт) не може мати одночасно точно
визначені координату х і імпульс р, причому невизначеності
цих величин задовольняють умову: добуток невизначеності координати та імпульсу не
може бути меншим за постійну Планка:
![]()
Нижче
наведений рисунок 2. 3, який ілюструє дане співвідношення.
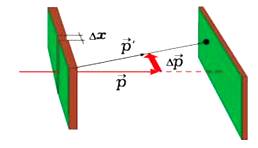
Рис. 2. 3
V.ІІ. Співвідношення невизначеності для
енергії частинок і часу їх взаємодії
Співвідношення невизначеності Гейзенберга можна узагальнити для інших канонічно спряжених
величин. Наприклад, для енергії
частинок і часу їх взаємодії: добуток
невизначеності енергії частинки та часу перебування частинки у стані з такою
енергією, не може бути меншим за постійну Планка:
![]()
V. III. Принципові положення квантової
механіки
1. Для опису мікрооб'єктів Н. Бор
сформулював у 1927 році принципове положення квантової механіки - принцип
додатковості: одержання експериментальних даних про якісь одні фізичні
величини, які описують мікрооб'єкт (елементарну частинку, атом, молекулу),
відповідно пов'язане з втратою даних про деякі інші фізичні величини, які є
додатковими до перших.
2. Стан системи мікрочастинок, визначений
у квантовій механіці, однозначно випливає з
попереднього стану, як того вимагає принцип причинності: у квантовій механіці стан мікрооб'єкта цілком визначається хвильовою
функцією. Задання хвильової функції для даного моменту часу визначає її
значення в наступні моменти.
3. Принцип відповідності Бора
(1923р.): усяка нова, більш загальна теорія, яка є розвитком класичної, не
спростовує її цілком, вказуючи границі її застосування, причому у для граничних
випадків відбувається перехід нової теорії у стару.