Т.8. Квантова статистика Фермі – Дірака

§1. Хвильова функція і енергія вільного електрона в металі

І.І. Хвильова функція вільного електрона у металі.

Квантова статистика Фермі – Дірака розроблена для вільних електронів у металі (електронів провідності).

Загальне рівняння Шредінгера для частинки, яка володіє енергією і рухається в потенціальному полі, має вигляд:

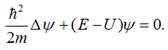
Враховуючи, що для вільного електрона U=0, стаціонарне рівняння Шредінгера для вільного електрона у кубічному зразку металу з ребром L запишемо:

Розв’язком такого диференціального рівняння є просторова хвильова функція, яка визначається виразом:

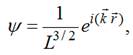
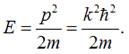
І.ІІ. Енергія вільного електрона в металі

Хвильова функція електрона буде неперервна і однозначна в об’ємі з ребром L, якщо компоненти вектора будуть мати вигляд:

де n_x, n_y, n_z – цілі числа, які незалежно одне від іншого можуть приймати значення:

Враховуючи, що у прямокутній системі координат хвильовий вектор електрона можна представити як:

Тому:

Тоді енергію вільного електрона в металі можна представити у вигляді:

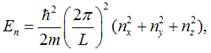
де n – головне квантове число електрона в металі, індекс біля n показує напрям руху електрона в прямокутній системі координат.

§2. Число станів електрона в металі, енергія яких не перевищує значення E_n. Густина станів електрона в металі

Введемо уявний фазовий простір з осями

Поверхня рівних енергій (яка об’єднує точки фазового простору з однаковими значеннями енергії) в такому просторі матиме форму сфери з радіусом:

Враховуючи принцип Паулі, число станів можливих для існування електрона у металі, енергія яких не перевищує значення E_n , рівне подвоєному об’єму сфери з радіусом n_E і визначається виразом:

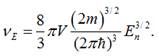
Знайдемо число можливих станів у інтервалі dE_n :

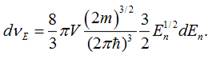
Після спрощення одержимо:

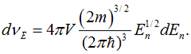
Густиною станів називають відношення числа станів, можливих для існування електрона у металі, в інтервалі dE_n до величини цього інтервалу:

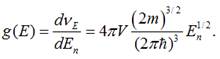
§3. Енергія Фермі

Енергія, нижче якої всі енергетичні рівні електронів у металі є заповнені при Т=0, називається енергією або рівнем Фермі при абсолютному нулеві і визначається виразом:

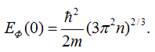
Енергія Фермі залежить від концентрації електронів у металі і враховуючи її середнє значення одержимо:

Зауваження:

1) середня енергія електронів у кристалі при абсолютному нулі:

2) середня швидкість електронів у кристалі при абсолютному нулі:

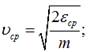
3) максимальна швидкість електронів у кристалі при абсолютному нулі:

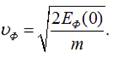
§4. Функція Фермі – Дірака

IV.І. Функція розподілу вільних електронів у металі по станах за енергіями називається функцією розподілу Фермі – Дірака:

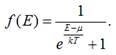
З фізичної точки зору f(E) являє собою густину ймовірності заповнення електронами рівня з енергією Е, або середнє число електронів, які знаходяться в стані з енергією Е:

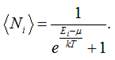
Зауваження. Частинки, що підлягають розподілу Фермі – Дірака мають півцілий спін і називаються ферміонами (електрони).

IV.ІІ. Властивості функції Фермі-Дірака при Т=0

Розглянемо функцію Фермі – Дірака:

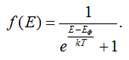
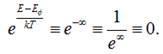
Тому:

Тому:

3. Графічне зображення функції Фермі – Дірака при Т=0 подано на рис. 8. 1:

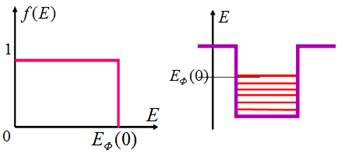
Рис. 8.1

Висновок. При Т=0 енергетичні рівні електронів у кристалі нижче рівня Фермі заповнені повністю з ймовірністю рівною одиниці. Рівні з енергією вищою за рівень Фермі заповнені з ймовірністю рівною нулю.

IV.ІІІ. Властивості функції Фермі – Дірака при Т>0

Враховуючи, що

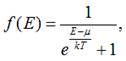
одержимо:

Висновок. Рівень Фермі при довільній температурі кристала співпадає з тим енергетичним рівнем електронів у кристалі, ймовірність заповнення якого рівна 1/2.

2. Графічне зображення функції Фермі – Дірака при Т≠0 подано на рис. 8. 2:

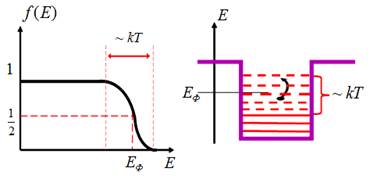
Ймовірність заповнення електронами енергетичних

рівнів при

Рис. 8. 2

Зауваження. Зміна значення функції Фермі – Дірака від 1 до 0 при Т≠0 відбувається в околі енергії Е_Ф для даного кристала.