Т.7. Квантова статистика Бозе-Ейнштейна і Максвела-Больцмана

§1. Поняття про статистичну фізику. Фазовий простір. Функція розподілу

Статистична фізика вивчає системи, що складаються з великого числа частинок (електрони в металі).

Класична неможливість описати рух всіх частинок системи вирішується статистичною фізикою, яка знаходить статистичні закономірності їх поведінки, а за ними визначає середні або ймовірні значення параметрів частинок.

І. І. Фазовий простір

Нехай система складається з N частинок. Для опису такої системи вводиться багатомірний простір, який являє собою багатомірну систему координат та імпульсів всіх частинок системи. Для кожної такої точки системи є 6N (три декартових координати та три проекції імпульсу точки). Такий 6N-мірний простір називається фазовим простором.

Для прикладу зобразимо фазовий простір (багатомірну систему координат) для системи, яка складається з однієї частинки (рис. 7.1).

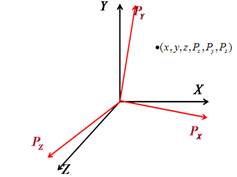
Рис. 7. 1

У фазовому просторі стан однієї частинки з координатами та проекціями імпульсу у довільний момент часу визначається однією точкою.

I. ІІ. Функція розподілу

1. Розіб’ємо фазовий простір на 6N-мірні елементарні комірки об’ємом

в якому:

dq – сукупність елементарних проміжків 3N координат усіх частинок системи;

dp – сукупність елементарних проміжків 3N проекцій імпульсу усіх частинок системи.

2. Відповідно до хвильової теорії і співвідношень невизначеності Гейзенберга, найменше значення об’єму елементарної комірки:

3. Ймовірність того, що певна точка фазового простору попаде у виділений елемент фазового об’єму визначається величиною:

4. Величина

називається функцією розподілу.

5. У відповідності з теорією ймовірності величина

називається густиною ймовірності існування певних станів системи.

У відповідності з попереднім:

Отже, функція розподілу є густиною ймовірності того, що певна точка фазового простору попаде в елементарний об’єм координат та проекцій імпульсу, який описує стан системи.

6. Загальну формулу для функції розподілу ймовірності існування різних станів системи встановив американський фізик В. Гібс (1839-1903). Так званий канонічний розподіл Гібса має вигляд:

А – постійна, що визначається з умови нормування функції розподілу до одиниці:

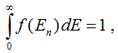
n – квантове число, яке характеризує стан системи з енергією .

§2. Порівняльна характеристика різних статистичних підходів

Загальний стан системи з N частинок з повною енергією Е називають макростаном системи.

Кожен макростан може мати набір мікростанів, які характеризують розподіл частинок по енергіях всередині системи.

Число мікростанів системи залежить:

-     від розрізненості частинок системи;

-     від того, чи можуть дві частинки знаходитись в одному стані.

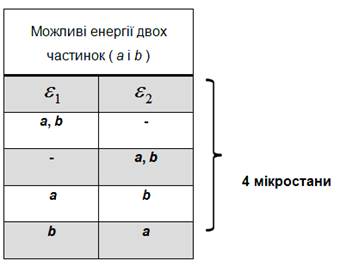
ІІ.І. За статистикою Максвела – Больцмана частинки розрізнимі і можуть займати довільні стани, приведені у таблиці:

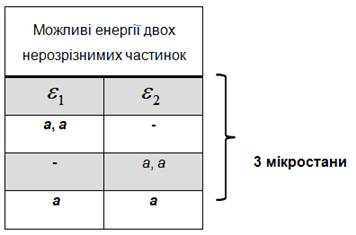
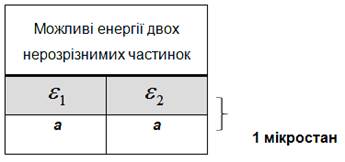
ІІ.ІІ. За статистикою Бозе – Ейнштейна частинки нерозрізнимі і можуть займати довільні стани, приведені у наступній таблиці:

ІІ.ІІІ. За статистикою Фермі – Дірака частинки нерозрізнимі і враховується принцип Паулі:

§3. Функція розподілу Бозе – Ейнштейна і її зв’язок з функцією Максвела – Больцмана

ІІІ. І. Функція розподілу Бозе – Ейнштейна:

- випливає з канонічного розподілу Гібса;

- з умов статистики Бозе – Ейнштейна для частинок з цілим спіном (фотони, фонони);

- має вигляд:

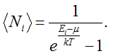
Тут – середнє число бозонів у квантовому стані, який має енергію,

– хімічний потенціал, який рівний зміні внутрішньої енергії системи при збільшенні в ній числа частинок на одиницю та фіксованих значеннях інших величин, від яких вона залежить.

Зауваження. Бозони – частинки з цілим або нульовим спіном

ІІІ. ІІ. Якщо енергія частинок набагато більша за хімічний потенціал системи:

тоді:

У формулі функції розподілу Бозе – Ейнштейна нехтуємо одиницею в знаменнику:

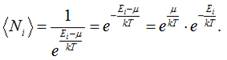
Проведемо заміну:

Тоді формула для матиме вигляд:

Одержали класичну функцію розподілу Максвела – Больцмана.

Висновок. При великих енергіях частинок системи, тобто, якщо виконується умова , функція розподілу Бозе – Ейнштейна переходить у класичну функцію Максвела – Больцмана.

Зауваження. Система частинок називається виродженою, якщо її властивості суттєво відрізняються від властивостей, які описує класична теорія (функція Бозе – Ейнштейна описує стан вироджених систем) .