РОЗДІЛ 2 МОДЕЛЮВАННЯ ЕЛЕКТРОННО-КОМУНІКАЦІЙНИХ СИСТЕМ

ТЕМА 1 ЗАГАЛЬНІ ПИТАННЯ ТЕОРІЇ МОДЕЛЮВАННЯ

Математичне моделювання полягає в перекладі явищ нашого «реального світу» мовою математики. Поняття «модель» відображає поведінку об’єкта або процесу. Крайніми випадками поняття «моделювання» є, з одного боку, натурний експеримент, з іншого, – розрахунково-аналітичний. Між ними є проміжні методи досліджень. Вони дозволяють скоротити і полегшити натурний експеримент.

Математичні моделі (ММ) поділяються на:

а) аналітичні, побудовані за фізичними законами і розкривають суть явищ;

б) експериментально-статистичні, що відповідають набору експериментальних даних.

Аналітичні моделі дозволяють отримати явні (аналітичні) залежності для необхідних величин або, якщо це неможливо, знайти чисельні рішення для конкретних початкових умов і кількісних характеристик моделі.

Експериментально-статистичні моделі слугують для опису об’єкта як «чорного ящика». Тому обґрунтування достовірності (верифікації) ММ є невід’ємною частиною застосування методів моделювання.

Модель зазвичай уточнюється шляхом постановки натурних експериментів, що підтверджують точність і достовірність ММ.

Збільшення складності ММ для забезпечення більшої точності результатів має природне обмеження з боку швидкості обробки інформації, пам’яттю ЕОМ. Так, якщо вихідні дані відомі з точністю до 5%, то безглуздо пропонувати моделі, що забезпечують точність рішення 1%.

Застосовуються методи математичного моделювання як до фізичних, так і до електричних процесів, а також і в галузях медицини, статистики тощо. Наприклад, розроблені моделі молекул, дорожнього руху тощо.

ММ технічного об’єкта – система математичних об’єктів (чисел, змінних, матриць, множин і т. п.) і відношень між ними, що відображає деякі властивості технічного об’єкта. У проектуванні використовують ММ, що відображають властивості об’єкта, суттєві з позицій інженера.

Серед властивостей об’єкта, що відображаються в описах на певному ієрархічному рівні, зокрема в ММ, розрізняють властивості систем, елементів систем і зовнішнього середовища, у якій має функціонувати об’єкт. Кількісне вираження цих властивостей здійснюється за допомогою величин, що називаються параметрами. Величини, що характеризують властивості системи, елементів системи та зовнішнього середовища, називають відповідно вихідними, внутрішніми і зовнішніми параметрами.

 

1 Вимоги до математичних моделей в електроніці

До ММ висуваються вимоги універсальності, адекватності, точності й економічності.

Ступінь універсальності ММ характеризує повноту відтворення в моделі властивостей реального об’єкта. ММ відображає лише деякі властивості об’єкта. Так, більшість ММ, використовуваних у функціональному проектуванні, призначені для відображення фізичних або інформаційних процесів, що відбуваються в об’єкті, водночас не потрібно, щоб ММ описувала такі властивості об’єкта, як геометрична форма його елементів. Наприклад, ММ резистора у вигляді рівняння закону Ома характеризує властивість резистора пропускати електричний струм, але не відображає габарити резистора як деталі, його колір, механічну міцність, вартість тощо. Нехай відображені в ММ властивості оцінюються вектором вихідних параметрів Y = (y₁, y₂,…y_m). Тоді, позначивши справжнє і розраховане за допомогою ММ значення j-го вихідного параметра через y_{j іст} і у_{j м} відповідно,  визначимо відносну похибку ε_j розрахунку параметра у_j як:

 

                                           (1)

 

Отримана векторна оцінка ε = (ε₁, ε₂,… ε_m) за необхідності зведення цієї оцінки до скалярної використовують будь-яку норму вектора ε, наприклад:

 

                                         (2) 

 

Адекватність ММ – здатність відображати задані властивості об’єкта з похибкою не вищою від заданої. Оскільки вихідні параметри є функціями векторів параметрів зовнішніх Q і внутрішніх X, похибка залежить від значень Q і X. Зазвичай значення внутрішніх параметрів ММ визначають з умови мінімізації похибки ε_М у деякій точці Q_НОМ простору зовнішніх змінних, а використовують модель із розрахованим вектором X за умови різних значень Q. У цьому випадку адекватність моделі має місце лише в обмеженій області зміни зовнішніх змінних – області адекватності (ОА) математичної моделі:

 

                                      (3)

де δ > 0 – задана константа, рівна гранично допустимій похибці моделі.

 

Економічність ММ характеризується витратами обчислювальних ресурсів (витратами машинних часу Т_м і пам’яті ПМ) на її реалізацію. Чим менші Тм і П_М, тим модель економічніша. Замість значень Т_м і П_М, що залежать не тільки від властивостей моделі, а й від особливостей застосовуваної ЕОМ, часто використовують інші величини, наприклад: середня кількість операцій, які виконуються в разі одного звернення до моделі, розмірність системи рівнянь, кількість використовуваних у моделі внутрішніх параметрів та ін.

Вимоги високої точності, ступеня універсальності, широкої області адекватності, з одного боку, і високої економічності, з іншого боку, суперечливі. Найкраще компромісне задоволення цих суперечливих вимог залежить від особливостей вирішуваних завдань, ієрархічного рівня й аспекту проектування.

 

2 Класифікація моделей в електроніці

За характером відображуваних властивостей об’єкта ММ поділяються на структурні та функціональні.

Структурні ММ призначені для відтворення структурних властивостей об’єкта. Серед структурних ММ розрізняють топологічні й геометричні.

У топологічних ММ відображаються склад і взаємозв’язки елементів об’єкта. Їх найчастіше застосовують для опису об’єктів, що складаються з великої кількості елементів, у вирішенні завдань прив’язки конструктивних елементів до певних просторових позиціях (наприклад, завдання компонування обладнання, розміщення деталей, трасування з’єднань) або до відносних моментів часу (наприклад, у розробці розкладів, технологічних процесів).

Топологічні моделі можуть мати форму графів, таблиць (матриць). У геометричних ММ відображаються геометричні властивості об’єктів, у них, крім відомостей про взаємне розташування елементів, містяться відомості про форму деталей. Геометричні ММ можуть виражатися сукупністю рівнянь ліній і поверхонь; алгебрологічних співвідношень, які описують області, що становлять тіло об’єкта; графами і списками, що відображають конструкції з типових конструктивних елементів та ін. Геометричні ММ застосовують для вирішення завдань конструювання в машинобудуванні, приладобудуванні, радіоелектроніці, для оформлення конструкторської документації, у завданні вихідних даних на розробку технологічних процесів виготовлення деталей.

Функціональні ММ призначені для відображення фізичних чи інформаційних процесів, що відбуваються в об’єкті за умови його функціонування або виготовлення. Зазвичай функціональні ММ є системами рівнянь, що зв’язують фазові змінні, внутрішні, зовнішні та вихідні параметри. Розподіл описів об’єктів на аспекти та ієрархічні рівні безпосередньо стосується математичних моделей. Виділення аспектів опису приводить до виділення моделей електричних, механічних, гідравлічних, оптичних, хімічних тощо. Зокрема моделі процесів функціонування виробів і моделі процесів їхнього виготовлення різні. Наприклад, моделі напівпровідникових елементів інтегральних схем, що описують процеси дифузії і дрейфу рухливих носіїв заряду в напівпровідникових областях під час функціонування приладу і процеси дифузії домішок у напівпровідниках у процесі виготовлення приладу.

Використання принципів блоково-ієрархічного підходу до проектування приводить до появи ієрархії математичних моделей проектованих об’єктів. Кількість ієрархічних рівнів у моделюванні визначається складністю проектованих об’єктів і можливістю засобів проектування.

Залежно від місця в ієрархії описів ММ поділяються на ті, що належать до мікро-, макро- і метарівня.

Особливістю ММ на мікрорівні є відображення фізичних процесів, що протікають в безперервних просторі та часі. Типові ММ на макрорівні – диференціальні рівняння в частинних похідних (ДРЧП). У них незалежними змінними є просторові координати і час. За допомогою цих рівнянь розраховуються поля механічних напруг і деформацій, електричних потенціалів, тисків, температур і т. п. Можливості застосування ММ у вигляді ДРЧП обмежені окремими деталями, спроби аналізувати з їхньою допомогою процеси в багатокомпонентних середовищах, складальних одиницях, електронних схемах не можуть бути успішними через надмірне зростання витрат машинного часу та пам’яті.

На макрорівні використовують збільшену дискретизацію простору за функціональною ознакою, що приводить до подання ММ на цьому рівні у вигляді систем звичайних диференціальних рівнянь (ЗДР). У цих рівняннях незалежною змінною є час t, а вектор залежних змінних V становлять фазові змінні, що характеризують стан укрупнених елементів дискретизованого простору. Такими змінними є сили і швидкості механічних систем, напруги й сили струму електричних систем, тиску та витрати гідравлічних і пневматичних систем тощо. Системи ЗДР є універсальними моделями на макрорівні, придатними для аналізу як динамічних, так і сталих об’єктів. Порядок системи рівнянь залежить від кількості виділених елементів об’єкта. Якщо порядок системи наближається до 10³, то оперування моделлю стає складним, і тому необхідно переходити до уявлень на метарівні.

На метарівні як елементи приймають досить складні сукупності деталей. Метарівень характеризується великою різноманітністю типів використовуваних ММ. Для багатьох об’єктів ММ на метарівні, як і раніше, представляються системами ЗДР. Однак, оскільки в моделях не описуються внутрішні для елементів фазові змінні, а фігурують тільки фазові змінні, що стосуються взаємних зв’язків елементів, то укрупнення елементів на метарівні означає отримання ММ прийнятної розмірності для істотно більш складних об’єктів, ніж на макрорівні.

У низці предметних галузей вдається використовувати специфічні особливості функціонування об’єктів для спрощення ММ. Прикладом є електронні пристрої цифрової автоматики, у яких можливо застосовувати дискретне уявлення таких фазових змінних, як напруги і струми. Унаслідок ММ стає системою логічних рівнянь, що описують процеси перетворення сигналів. Такі логічні моделі істотно більш економічні, ніж моделі електричні, що описують зміни напруг і сил струмів як безперервних функцій часу. Важливий клас ММ на метарівні становлять моделі масового обслуговування, що застосовуються для опису процесів функціонування інформаційних і обчислювальних систем, виробничих ділянок, ліній і цехів.

Структурні моделі також поділяються на моделі різних ієрархічних рівнів. Водночас на нижчих ієрархічних рівнях переважає використання геометричних моделей, на вищих ієрархічних рівнях застосовуються топологічні моделі. За ступенем деталізації опису в межах кожного ієрархічного рівня виокремлюють повні ММ і макромоделі.

Повна ММ – модель, у якій фігурують фазові змінні, що характеризують стан усіх наявних міжелементних зв’язків (тобто стан усіх елементів проектованого об’єкта).

Макромодель – ММ, у якій відображається стан значно меншої кількості міжелементних зв’язків, що відповідає опису об’єкта за умови збільшеного виділення елементів.

За способом подання властивостей об’єкта функціональні ММ поділяються на аналітичні та алгоритмічні.

Аналітичні ММ є явними виразами вихідних параметрів як функцій вхідних і внутрішніх параметрів. Такі ММ характеризуються високою економічністю, однак, як правило, вимагають прийняття істотних припущень і обмежень, що знижують точність і звужують область адекватності моделі.

Алгоритмічні ММ відтворюють зв’язок вихідних параметрів з параметрами внутрішніми та зовнішніми у формі алгоритму.

Імітаційна ММ – алгоритмічна модель, що відображає поведінку досліджуваного об’єкта в часі в разі задання зовнішніх впливів на об’єкт. Прикладами імітаційних ММ можуть слугувати моделі динамічних об’єктів у вигляді систем ЗДР і моделі систем масового обслуговування, задані в алгоритмічній формі.

Для отримання ММ використовують методи неформальні й формальні. Неформальні застосовують на різних ієрархічних рівнях для отримання

ММ елементів. Ці методи передбачають вивчення закономірностей процесів і явищ, пов’язаних з об’єктом, що моделюється, виділення істотних чинників, прийняття різного роду припущень та їхнього обґрунтування, математичну інтерпретацію наявних відомостей тощо. Для виконання цих операцій у загальному випадку відсутні формальні методи, водночас від результату цих операцій істотно залежать показники ефективності ММ – ступінь універсальності, точність, економічність. Тому побудова ММ елементів, як правило, здійснюється кваліфікованими фахівцями, які пройшли підготовку як у відпо-відній предметній галузі, так і в питаннях математичного моделювання на ЕОМ.

Застосування неформальних методів можливе для синтезу ММ теоретичних і емпіричних. Теоретичні ММ створюються внаслідок дослідження процесів і їхніх закономірностей, властивих класу об’єктів і явищ, що розглядаються; емпіричні ММ – після вивчення зовнішніх проявів властивостей об’єкта за допомогою вимірювань фазових змінних на зовнішніх входах і виходах та обробки результатів вимірювань.

Вирішення завдань моделювання елементів полегшується завдяки тому, що для побудови більшості технічних об’єктів використовуються типові елементи (кількість типів порівняно невелика). Тому розробка ММ елементів проводиться порівняно рідко. Один раз створені ММ елементів надалі багаторазово застосовують у розробці різноманітних систем із цих елементів. Прикладами таких ММ на мікрорівні є опис кінцевих елементів для аналізу напружено-деформованого стану деталей, безліч типів кінцевих елементів містять стрижні, плоскі елементи у формі трикутників і чотирикутників, тривимірні елементи типу паралелепіпеда, тетраедра тощо. Прикладами ММ геометричних елементів можуть бути рівняння ліній прямих, дуг кіл, площин і поверхонь другого порядку. Прикладами ММ елементів на макрорівні є ММ елементів інтегральних схем – транзисторів, діодів, резисторів, конденсаторів.

Формальні методи застосовують для отримання ММ систем у разі відомих математичних моделей елементів.Отже, у програмах автоматизованого аналізу, що використовуються в САПР, отримання ММ проектованих об’єктів забезпечується реалізацією ММ елементів і методів формування ММ систем.

 

3 Методика отримання математичних моделей елементів

У загальному випадку процедура отримання математичних моделей елементів передбачає певні операції. Перелічимо їх.

1.         Вибір властивостей об’єкта, які підлягають відображенню в моделі. Цей вибір оснований на аналізі можливих застосувань моделі та визначає ступінь універсальності ММ.

2.        Збір вихідної інформації про обрані властивості об’єкта. Джерелами відомостей можуть бути досвід і знання інженера, який розробляє модель, науково-технічна література, насамперед довідкова, опис прототипів – наявних ММ для елементів, близьких за своїми властивостями до досліджуваного, результати експериментального вимірювання параметрів тощо.

3.        Синтез структури ММ. Структура ММ – загальний вигляд математичних співвідношень моделі без конкретизації числових значень параметрів. Структура моделі може бути представлена також у графічній формі, наприклад у вигляді еквівалентної схеми або графа. Синтез структури – найбільш відповідальна операція й вона з найбільшими труднощами піддається формалізації.

4.        Розрахунок числових значень параметрів ММ. Ця задача ставиться як задача мінімізації похибки моделі заданої структури, тобто:

 

                                            (4)

 

де X – вектор параметрів моделі; ХД – область варіювання параметрів; визначається відповідно до (1) і (2), де y_{j M} – функція від X, а y_{j іст} визначаються за результатами експериментів або фізичних, або чисельних із використанням більш точних ММ, якщо такі є в ієрархічному ряді ММ.

5. Оцінка точності й адекватності ММ. Для цього мають використовуватися значення yj іст, які не фігурували у розв’язанні задачі (3).

 

4 Аналітичні моделі

Аналітична модель системи описує її функціонування за допомогою математичних об'єктів. Така модель будується на основі понять і символіки однієї з теорій, наприклад, теорії масового обслуговування або теорії ланцюгів Маркова. Якщо обрані показники якості системи вдається явно виразити в залежності від параметрів моделі, то говорять, що має місце аналітичне рішення. Важлива перевага аналітичних рішень полягає в тому, що вони дозволяють швидко і з мінімальними витратами отримати значення показників якості в широкому діапазоні зміни вхідних параметрів моделі.

Застосовуючи моделі теорії масового обслуговування для оцінювання якості функціонування системи, будемо розглядати дану систему як сукупність обслуговуючих пристроїв. Як пристрої використовують різні ресурси системи – центральний процесор, оперативну пам'ять, зовнішні запам'ятовуючі пристрої, канали, пристрої введення-виведення та ін. Завдання або програми подають запити чи заявки на обслуговування до цих ресурсів або до обслуговуючих пристроїв. Тому значна частина задач оцінювання якості пов'язана з аналізом черг, що виникають як наслідок широко застосовуваного в інформаційно-телекомунікаційних системах принципу поділу ресурсів серед багатьох користувачів, програм і процесів.

    

5 Імітаційні моделі

Імітаційна модель системи описує її функціонування у вигляді послідовності операцій чи груп операцій, які виконуються на ЕОМ. Складовими частинами імітаційної моделі є описи елементів, що утворюють систему, і опис структури системи, тобто сукупності зв'язків між елементами. Ці описи подаються у вигляді алгоритмів, на основі яких розробляється програма для ЕОМ.

Отже, імітаційну модель можна реалізувати як програму, а імітаційне моделювання звести до проведення експериментів на ЕОМ шляхом прогонки цієї програми на деякій множині вхідних даних.

Трасою називають потік подій, які мають місце під час роботи системи та реєструються у хронологічному порядку, що часто збігається із моментами їхнього виникнення.

Траса, яку використовують для моделювання, повинна досить добре відображати робоче завантаження (типові умови роботи) обчислювальної системи, причому треба мати на увазі, що на трасі позначаються не тільки особливості машини, але і особливості трасованих програм.

Суттєва перевага імітаційної моделі порівняно з аналітичною полягає в тому, що за рахунок ускладнення цієї моделі її можна зробити як завгодно наближеною до реального об'єкта чи навіть досягти повного збігу моделі з об'єктом.

Однак найчастіше на розробку імітаційної моделі витрачають значно більше часу, а програма, що вийшла, вимагає значно більше машинних ресурсів і дає значно менше інформації, ніж очікувалося спочатку. Тому імітаційне моделювання рекомендовано до застосовування тільки в тих випадках, коли задачі оцінювання якості системи настільки складні, що аналітичний підхід виявляється непридатним.

 

ТЕМА 2 МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ ЕЛЕКТРОННИХ ПРИЛАДІВ

1 Змінні Ейлера та Лагранжа

Як відомо, робота електронних ламп основана на використанні руху електронів під дією електричних полів. Побудова ММ електронного приладу (ЕП) є індивідуальним завданням для кожного виду ЕП. Однак існує низка загальних закономірностей, характерних для будь-якого типу (як електро-вакуумних, так і напівпровідникових) приладів.

Насамперед зупинимося на двох уявленнях математичного опису руху електронного потоку. Як правило, процес взаємодії в ЕП пов’язаний із впливом електронного потоку на електромагнітне або електростатичне поле: знання поведінки цього потоку визначає успіх побудови ММ ЕП.

Нехай траєкторія руху електронів описується рівнянням:

 

                                          (1)

 

Якщо в цьому випадку нас не цікавить шлях, який описують окремі частинки, то (1) є траєкторією деякого потоку (подібний підхід характерний для гідродинаміки), що вивчається стороннім спостерігачем, який знаходиться в нерухомій лабораторній системі координат. Змінні x, y, z, t називаються ейлерові (змінні Ейлера). У цьому випадку поняття щільності струму і заряду мають прямий фізичний зміст, оскільки вони характеризують стан потоку в окремих точках простору. Однак у деяких випадках необхідно знати швидкості та розташування окремих зарядів у потоці, що обумовлено неламінарним їхнім рухом у просторі. Тоді використовують лагранжеві змінні, коли змінними є поточний час t (або поточна координата) і проміжок часу tо влітання частки в область взаємодії. Інакше, змінні Лагранжа пов’язані з рухом частинки, тобто характеризують рухому систему координат.

З точки зору формального підходу змінні Ейлера слід ототожнювати із спостерігачем, що знаходиться в деякій фіксованій системі координат, щодо якої відбувається рух електронного потоку й окремих частинок у ньому, у той час як змінні Лагранжа ототожнюються із спостерігачем, пов’язаним безпосередньо з частинками, які переміщуються. На практиці це еквівалентно в першому випадку спостерігачеві, який дивиться з тротуару на наповнений людьми автобус, що проходить, а в другому випадку спостерігач знаходиться вже в автобусі й дивиться на людину, яка стоїть на тротуарі.

          Розглянемо взаємозв’язок змінних Ейлера і Лагранжа на прикладі руху потоку електронів в одновимірному діодному проміжку (рис. 1). Припустимо, що електрони влітають у простір, обмежений площинами z ϵ [0, d], протягом якогось проміжку часу Т, і для кожного електрона є рівняння траєкторії

 

                                                         (2)

 

яке задовольняє умові Z = (τ, τ) = Z= (τ, t)_t-τ =0.

Тут τ – час влітання електрона в доданий проміжок (проміжок часу). Оскільки ми не обговорюємо умови руху кожного окремого електрона, у процесі їхнього пересування відбуваються якісь еволюції і в певний момент часу t в області, обмеженою площинами Р і Q, зосередиться заряд

 

                                              (3)

 

де – об’ємна щільність заряду. Ця умова зрозуміла, оскільки заздалегідь передбачається постановка одновимірної задачі, тобто незалежність процесів від координат X і Y.

 

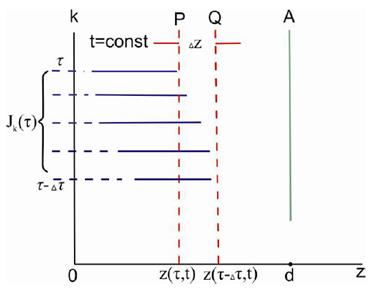
Рисунок 1 – Електронний потік у плоскому діоді

 

На площині Р знаходяться електрони, що влетіли в доданий проміжок у деякий початковий момент часу, а площину Q досягнуть електрони, які вилетіли раніше на час Δτ (тобто, якщо початковий час τ – Δτ).

Отже, ширина проміжку визначається сукупністю двох груп електронів, траєкторії яких описуються рівняннями:

 

Тоді

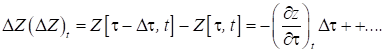
Електрони, які на момент t заповнили простір між площинами Р і Q, вилетіли з катода в інтервалі часу Δτ  і принесли заряд:

 

                                                (4)

 

де j_к(τ) – густина конвекційного струму в площині влітання електронів у доданий проміжок. Відповідно до закону збереження заряду:

 

 

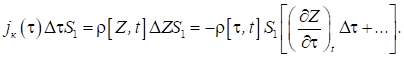
Розділивши обидві частини на ΔτS₁ і здійснивши перехід до межі за умови Δτ→0, отримуємо:

 

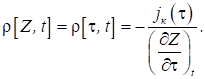                                                   (5)

 

Отже, якщо відомі закони зміни густини струму й закон руху заряду, то можна розраховувати щільність об’ємного заряду в будь-який фіксований час.

      У нашому випадку змінні, у яких незалежні величини – початковий чаc електронів і поточний час t, є лагранжеві та позначаються (τ, t), а змінні Z і t – ейлерові змінні – позначаються [Z, t], запис (∂z/∂τ)_t означає диференціювання за умови фіксованого часу t, а (∂z/∂τ)_τ – у разі фіксованого τ.

      Оскільки найбільш загальним в електроніці випадком є опис електронів (або інших заряджених частинок) у вигляді деякої кінематичної субстанції, розглянемо зміст основних понять механіки.

      За своїм змістом швидкість і прискорення – це характеристики окремої матеріальної точки, тобто їх необхідно обчислювати, слідуючи за рухом окремого електрона, який вийшов в проміжок в момент часу.

      Інакше кажучи, у цих обчисленнях повної похідної постійної залишається, а змінюється поточний час t. Отже:

 

 

 

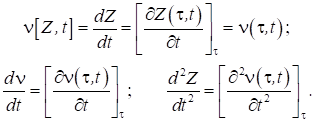
         Установимо деякі загальні правила переходу одних змінних в інші. Нехай задана функція F[z, t] у змінних Ейлера. Тоді, з урахуванням (1)

 

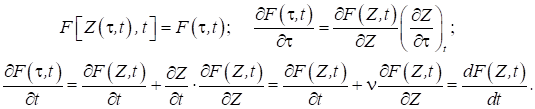    (6)

   

         Повний диференціал у змінних Лагранжа

 

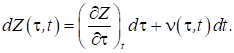                                (7)

 

є величиною першого порядку малості в збільшенні ΔZ(τ, t) = Z(τ, t) – Z(τ–Δτ,   t–Δt), що дорівнює відстані між двома різними електронами потоку: один увійшов у діодний проміжок пізніше та знаходиться там в момент t; інший увійшов під час τ–Δτ, а розглядається в момент t–Δt.

Подібний підхід дозволяє визначити щільність струму в будь-якій площині перетину діода (наприклад, у площині Р) за заданим законом інжекції струму за умови Z=0. Дійсно, нехай за час ∂τ у діод проникає заряд j_k(τ) ∂τ, який у вигляді щільності струму проходить через площину Р за час ∂t. Тоді відповідно до закону збереження заряду, маємо

 

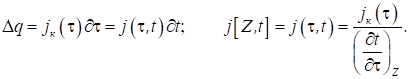                   (8)

 

Це співвідношення доводять інакше. Оскільки j[z, t] = νρ[z, t]‧ F[z, t], то з урахуванням (4)

 

                                                    

 

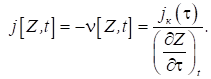
Для визначення густини струму в заданому перетині Р (7) потрібно

 

            

 

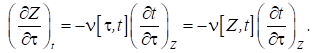
Змінні Лагранжа можуть бути не тільки (τ, t), а й (t, Z). Для цього досить скористатися рівнянням t = t(Z, τ), яке є іншою формою запису рівняння траєкторії частинки (1).

За своєю природою саме рівняння руху частинок представляються в лагранжевих змінних, а макроскопічні рівняння електродинаміки (рівняння Максвелла) потребують використання ейлерових змінних.

 

2 Моделювання електровакуумних приладів

Проектування електровакуумного приладу (ЕВП) пов’язане зі значними труднощами. Можна виділити основні елементи, притаманні всім типам ЕВП:

– інжектор електронів (катод або емітер);

– простір взаємодії, де взаємодіють потік електронів і електростатичні та (або) електромагнітні поля;

– колектор (анод), що збирає «відпрацьовані» електрони;

– балон, що обмежує область вакуумного середовища від повітряного.

Таке розмежування дозволяє спростити проектування всього ЕВП шляхом роздільного моделювання його основних елементів – зробити декомпозицію моделі. Наприклад, уся модель ЕВП буде складатися з чотирьох самостійних блоків. Інжектор електронів є або окремим електродом (наприклад, термоемісійний катод, найчастіше зустрічається в електронних лампах), або цілим пристроєм – електронною гарматою (в електронно-променевих і НВЧ-приладах). Метою цього елемента є створення потоку електронів, сформульо-ваного в необхідному для використання в даному ЕВП вигляді.

Так, для вакуумних діодів або інших типів ламп потрібно лише забезпечення емісії заданого числа електронів, в ЕВП і деяких приладах НВЧ до пучка, як правило, ставляться вимоги аксіальної симетрії (циліндричні суцільні або трубчасті пучки) тощо.

Розрахунок і конструювання інжекторів електронів є самостійною і часто оригінальною частиною моделювання ЕП. Колектор електронів (анод) відіграє роль елемента, що збирає «відпрацьовані» електрони. Його розрахунок зводиться здебільшого до визначення теплового режиму (потужності, що розсіюється на аноді).

Однак у деяких приладах НВЧ роль колектора значно тонша, оскільки шляхом створення певного розподілу потенціалу (рекуперація електронів) вдається підвищити ККД приладів.

 

3 Моделювання тріода

Побудова моделі тріода може йти по двох напрямках. Перший – аналітичне моделювання, основане на досить добре розробленій теорії процесів у тріодах на низьких частотах (приймально-підсилювальні та генераторні тріоди). Його перевага полягає в простоті, наочності і в задовільній якості результатів розрахунку та експерименту.

Недоліком цього напрямку є його наближеність, оскільки аналітичні рішення можуть бути отримані лише для найбільш простих часткових випадків геометрії приладу (плоского або циліндричного), у той час як реальна конструкція може мати суттєві відмінності. Наведемо основні елементи аналітичної моделі. Суть проектування полягає у визначенні геометрії приладу, що забезпечує необхідні статичні характеристики тріода, головним чином анодно-сіткові. Звідси випливає основне рівняння аналітичної моделі – закон степеня 3/2 для тріода:

 

                                               (9)

 

де σ = (1+ D + 1,33D')^-1 – гострота керування; G – первеанс пучка в тріоді; D – проникність сітки (для плоскої моделі рідкої сітки):

 

 

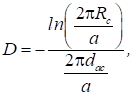
де R_c – радіус дроту сітки; a – крок намотки; d_ac – відстань анод-сітка).

У загальному вигляді можна представити:

 

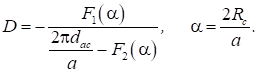                              (10)

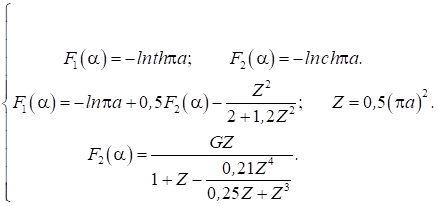
D^/ – обернена проникність сітки

 

  

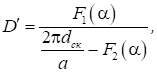
d_CK – відстань сітка-катод.

Якщо сітка рідка, то рівняння (9) видозмінюється:

 

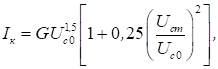
де

 

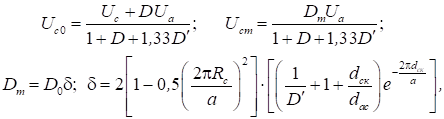
що справедливо для

У режимі від’ємної сіткової напруги струм катода I_к приблизно дорівнює анодному I_а. Однак, якщо U_c>0, необхідно враховувати режими повернення і прямого струмоперехоплення електронів і оперувати з коефіцієнтами

 

 

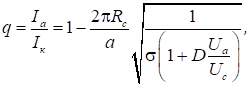
для режиму прямого струму перехоплення, коли 0 ≤ U_c ≤ U_a,

 

 

для режиму повернення, якщо U_a > U_c.

 

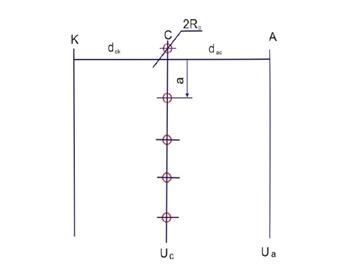
Рисунок 2 – Схема тріода

 

Наведені співвідношення є схемою аналітичної моделі та не враховують наявність динатронного ефекту та великої густини струму.

          4 Імітаційна модель тріода

Імітаційна модель тріода – більш високий ступінь моделі. На відміну від аналітичної, вона дозволяє вивчити такі тонкі ефекти, як струмоперехоплення електронів сіткою, врахувати початкові швидкості електронів тощо.

Побудова імітаційної моделі будь-якого вакуумного приладу основана на розв’язанні рівняння руху (другого рівняння Ньютона):

 

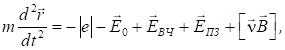                                  (12)

 

де r – радіус-вектор траєкторії електрона; Е₀ – вектор напруженості електростатичного поля; Е₀, Е_вч, Е_ПЗ – вектори напруженостей електричної складової електромагнітного поля і поля просторового заряду; В – вектор магнітної індукціі.

Для тріода, у статичному режимі та (12) матиме вигляд

 

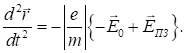                                         (13)

 

Отже, для визначення траєкторій руху електронів необхідно знати розподіл зовнішнього електростатичного поля і поля просторового заряду. Оскільки в тріодах у разі малої густини струму дія сил просторового заряду незначна, припустимо, що Е_ПЗ = 0  та з (13) перейдемо до:

 

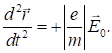                                                                                        (14)

 

Істотним фактом є те, що для побудови імітаційної моделі необхідно знати розподіл електростатичного поля в тріоді. У загальному випадку – це складна самостійна задача, що полягає у розв’язанні рівняння Лапласа

 

 

де

                                              (15)

 

U – розподіл потенціалу із заданими граничними умовами: U = 0 – на катоді, U=U_c – на границі сітки, U=U_a – на аноді.

Часто немає необхідності шукати аналітичне розв’язання рівняння (15), оскільки легше визначати розподіл потенціалу окремо яким-небудь із відомих чисельних методів (методом R-функцій, варіаційним, методом Монте-Карло або сітковим методом та іншими, вводячи в пам’ять ЕОМ необхідні значення U(P)). Нехай P = l₁ξ + l₂η, де l₁, l₂ – орти, а ξ і η – деякі довільні координати. Тоді:

 

 

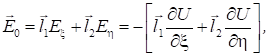
і, користуючись правилами векторної алгебри, отримаємо

 

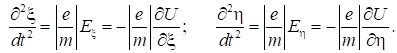                (16)

 

з граничними умовами на катоді ξ = ξ₀, η = η₀, dξ/dt =ξ₀^/, d η /dt = η^/.  

Найчастіше як початкові швидкості можна брати їхні теплові величини (KT/m)^1/2. Рівняння (16) описують рух кожної окремої частки, тому за своєю природою мають описуватися змінними Лагранжа. Для чисельної реалізації доцільно перетворити (16) до системи чотирьох рівнянь першого порядку шляхів заміни змінних

 

 

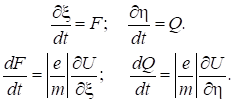
Остання система вирішується з урахуванням таких умов: якщо електрон потрапляє в область сітки, яка визначається координатами ξ_c, η_c він виключається з подальшого розрахунку; рахунок ведеться до потрапляння електрона на анод ξ_a, η_a величина струму визначається як сума частинок, що потрапили на електрод за певний інтервал часу:

 

 

Величина кожного заряду, що пналежить частинці, визначається, як правило, з емісійних характеристик катода. Так, якщо густина емісії 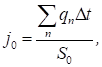  то величина заряду  де n – число частинок, що підлягають аналізу. Для усереднення значень інтервал необхідно брати значно більший, ніж крок інтегрування.

Для спрощення розрахунків і отримання універсальних траєкторій і струмів доцільно віднормувати величини в рівнянні (17). Наприклад, можна ввести 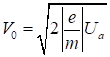 – швидкість електрона в площині анода,

       

 

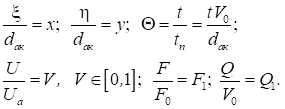
Тоді

 

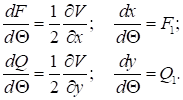                                     (17)

 

5 Модель напівпровідникового діода

Побудову найпростішої моделі напівпровідникового діода наведемо для одновимірного випадку, вважаючи, що всі процеси протікають лише в напрямку осі x , що є нормаллю до площини розділу p- і n-областей.

Уявімо діод у вигляді трьох секцій (рис.3): якщо x < x₁ p-область; в інтервалі x₁ < x < x₂ збіднена рухливими носіями область p-n  переходу (інакше вона називається областю просторового заряду); якщо x > x₂ n-область. Поверхні x₁ та x₂ характеризують границю збідненої області в р- і n-напів-провіднику відповідно.

 

Рисунок 3 – Схема напівпровідникового діода

 

Для одновимірної моделі вихідні рівняння приймають такий вигляд:

 

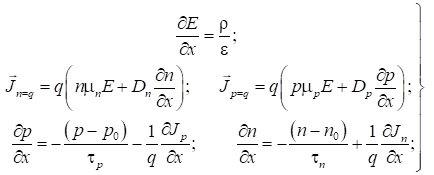         (18)

Спрощення цієї системи рівнянь пов’язані з низкою фізичних припущень, основаних на експериментальному вивченні властивостей напівпровідників. Як правило, р-область легована значно сильніше, ніж n-область, що дозволяє виключити з розгляду друге і п’яте рівняння системи. Крім того, у збідненій області дрейфовий і дифузійний струми дірок мають приблизно однакову величину, то з третього рівняння випливає, що τ_р = 0.

 

 

З урахуванням співвідношення Ейнштейна:

 

 

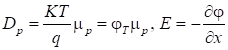
співвідношення (5) набуває вигляду:

 

                                            (19)

 

Інтегруючи рівняння (6), з урахуванням умов на границях із координатами x_p, x_n отримуємо:

 

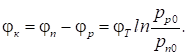                                     (20)

 

Отже, відповідно до (19) у рівноважному стані концентрація однотипних носіїв по обидві сторони переходу пов’язані співвідношеннями:

 

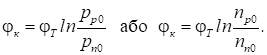                           (21)

 

Підставляючи замість контактної різниці потенціалів значення висоти потенційного бар’єра , яке відповідає порушенню рівноваги, отримуємо (φ_k±U):

 

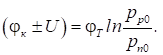                                    (22)

 

Тут знак «мінус» відповідає прямому включенню p-n-переходу; p_n – нерівноважна концентрація дірок, інжектованих в n-область, на границі n-області за умови x = x_n; φ_T – потенціал переходу в разі температури Т.

      Розв’язання (20) і (21) щодо P_n0 і p_n дає такі результати:

 

 

Звідки:

 

                                             (23)

 

Розв’язання рівняння (23) для концентрації електронів дає співвідношення нерівноважної концентрації електронів, інжектованих у p-область, на границі х = - х_р:

 

                                              (24)

 

Значення закону зміни концентрації дозволяє визначити статичну вольт- амперну характеристику діода. Для цього припустимо, що n-область електрично нейтральна, тобто струм у ній визначається тільки дифузійними процесами. Тоді J_P = |e|·D_p ·∂P/ ∂x, враховуючи, що ∂P/ ∂t = 0, отримуємо:

 

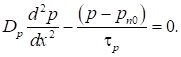
Розв’язання цього рівняння, з урахуванням (24) і за умови виконання граничних умов  має вигляд

 

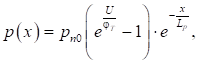                                   (25)

 

де L_P =(D_P·τ_P)^0,5 – дифузійна довжина хвилі в n-області.

Визначаючи з (25) похідну dp/dx і підставляючи її в рівняння для струму, знаходимо вираз для статичного струму діода

 

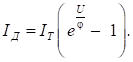                                          (26)

 

Тут враховано, що струм діода однаковий для площі S₀ за умови будь-якого x; a І_Т  = q‧D_P‧p_n0 ‧S₀ / L_P – тепловий струм.

Цікаво відзначити, що, з огляду на симетрії рівнянь для дірок і електронів, аналогічну залежність можна було б отримати, якщо розглядати тільки струм інжекції електронів n в p-область, але І_Т  = q‧D_P‧n_p0 ‧S₀ / L_P. Враховуючи також, що сумарний струм діода складається з суперпозиції діркової та електронної складових, вигляд результуючої залежності струму діода зберігається, тільки

 

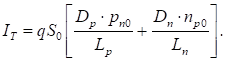                                    (27)

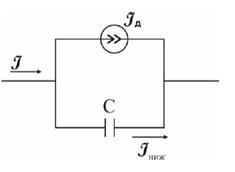
Рисунок 4 – Спрощена еквівалентна схема напівпровідникового діода

 

Отже, рівняння (26) і (27) становлять математичну модель діода в статичному режимі. Для побудови динамічної характеристики діода необхідно врахувати інерційні властивості p-n-переходу, обумовлені протіканням струму, що забезпечує зміна неосновних носіїв у базі діода, і струму, що забезпечує зміна об’ємної щільності просторового заряду іонізованих атомів домішок у збіднених областях. На еквівалентній схемі діода ці процеси описуються введенням ємності p-n переходу (рис. 4).

Не вдаючись у подробиці визначення виразу для ємності С, відзначимо, що ця ємність є паралельним включенням двох складових: дифузійної ємності:

 

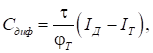                                 (28)

 

що характеризує зміну заряду неосновних носіїв при варіації потенціалу і бар’єрної ємності, яка характеризує зміну об’ємної густини просторового заряду у збідненій області.

 

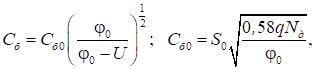                    (29)

 

а для плавного лінійного переходу (N_д = ax):

 

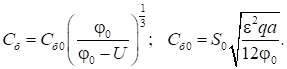                       (30)

 

Тут S₀ – площа поперечного перерізу р-n переходу, загальна ємність         С = С_диф + С_б, а загальний струм переходу

 

                                       (31)

 

Ідеалізовані вольт-амперні характеристики діода будуть відрізнятися від реальних, оскільки в отриманні формул не враховувалися деякі фізичні ефекти (наприклад, генерація і рекомбінація неосновних носіїв у збідненій області, наявність струмів витоків, інерційність установлення прямого опору діода в разі його включення, не враховано явища пробою p-n-переходу тощо).

 

6 Модель біполярного транзистора

Біполярний транзистор є сукупністю двох p-n-переходів, виконаних в одному кристалі напівпровідника й розділених тонкою базою. Фізико-топологічні моделі транзистора найбільш точні та універсальні. Залежно від того, за скількома координатами розглядаються фізичні процеси, моделі поділяються на одно-, дво- і тривимірні. Раніше було показано, що фізичні процеси в напівпровідниках описуються системою диференціальних рівнянь у частинних похідних, що містить рівняння безперервності для електронів і дірок та рівняння Пуассона:

 

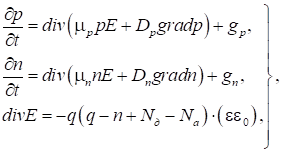                           (32)

 

де μ_p і μ_n – рухливості дірок і електронів; Dp і Dn – коефіцієнти дифузії дірок і електронів;  gp і gn – швидкості процесів генерації-рекомбінації дірок і електронів; q – заряд електрона; N_д і N_а – концентрації донорних і акцепторних легуючих домішок; ε – відносна діелектрична проникність напівпровідника; ε₀ – діелектрична постійна вакууму.

Невідомі функції цієї системи – концентрація дірок і електронів р(х, у, z, t) і п(х, у, z, t) і напруженість електричного поля Е(х, у, z, t). Замість Е може фігурувати електричний потенціал (х, у, z, t ), оскільки Е = – grad φ.

Крайові умови складаються з початкових умов, що характеризують розподіл залежних змінних за об’ємом кристала в початковий момент часу, і граничних, які задають значення залежних змінних на границях даної напівпровідникової області. Геометричні розміри і конфігурація дифузійних областей і омічних контактів транзистора також враховуються граничними умовами. Параметрами цієї моделі є основні електрофізичні параметри напівпровідника.

Диференціальні рівняння в частинних похідних можна розв’язувати методами кінцевих різниць або кінцевих елементів. За допомогою фізико-топо-логічної моделі можна з високим ступенем точності визначити основні статичні та динамічні характеристики транзистора.

Модель не враховує впливу магнітного поля та можливих неоднорідностей напівпровідникового матеріалу, що несуттєво для моделювання реальних транзисторів, оскільки більше значення має точне визначення параметрів моделі. Застосування подібних моделей транзистора в задачах аналізу електронних схем практично не реалізовується. Вони використовуються тільки для ідентифікації параметрів більш простих схемних моделей транзистора.

Схемні моделі транзистора основані, як правило, на істотних спрощеннях порівняно з фізикотопологічними моделями, тому дуже важливо чітко уявляти сферу застосування кожної такої моделі.

Найбільш поширені моделі отримані в одновимірному наближенні для сплавного бездрейфового транзистора, якому властива симетрична структура щодо бази – приблизно однакові площі емітерного і колекторного переходів. Транзистори цього типу працюють за умови низьких рівней інжекції, мають приблизно рівні концентрації домішок у емітера і колектора, основним механізмом переміщення носіїв через базу є дифузія, дрейфом носіїв нехтують. Розглянемо моделі – багатосекційну Лінвілла і програми ПА-1 (до цього ж класу належить відома модель Еберса–Молла), отримані для цих умов і основані на одновимірному поданні процесів, що відбуваються в транзисторі.

Модель Лінвілла характеризується тим, що основні рівняння в частинних похідних (32) замінюються системою ЗДР, які виходять наближеною заміною просторових похідних різницевими формулами. Заміна рівносильна поділу одновимірної р-n-р або n-р-n-cтруктури транзистора на ряд секцій кінцевих розмірів (рис. 5, а, б).

 

Рисунок 5 – Розподіл струмів у базі n-р-n-транзистора (а) і елементарна ділянка бази (б) в одновимірному наближенні

 

У межах кожної секції виходить система ЗДР, яку можна зіставити з формальною еквівалентною схемою (рис.4). Для отримання цієї схеми в (32) здійснюється перехід від концентрацій до потенціалів за формулами:

 

 

де n_і – власна концентрація; φ_p і φ_n – квазіпотенціали Фермі відповідно для дірок і електронів; W – електростатичний потенціал; φ_Т – температурний потенціал; φ_T = КТ/q; К – постійна Больцмана; Т – абсолютна температура.

Для кожної i-ї елементарної області (рис. 6, б) прийняті відповідні усереднені значення фізичних параметрів (Ni, μ_i тощо).

Невідомими функціями в цій моделі є квазіпотенціали Фермі φ_pi і φ_ni електростатичний потенціал Ψ_i. Елементи еквівалентної схеми відповідають певним членам у перетворених рівняннях (32) і мають відомий фізичний зміст. Елемент I_P відображає рекомбінацію електронів з дірками в i-й секції, C_ni – накопичення носіїв у ній, I_nj дифузію і дрейф носіїв з i-ї секції в (i+1)-ю, Сj – ємність струму зміщення.

 

 

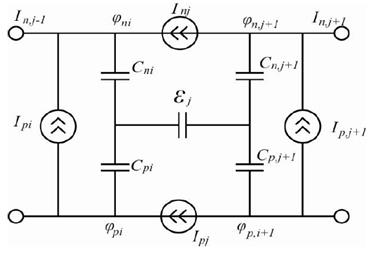
Рисунок 6 – Еквівалентна схема однієї секції моделі Лінвілла

 

Аналогічні елементи з індексом р відображають ті самі процеси, пов’язані з дірками в даній ділянці напівпровідника. Із секцій можна скласти ланцюг, що є одновимірною розподіленою моделлю транзистора.

Кількість секцій вибирається, виходячи з градієнта концентрації носіїв у конкретних ділянках кристала. Області з великим градієнтом концентрації (наприклад, область переходу) представлені великою кількістю секцій. Параметри цієї моделі – основні електрофізичні параметри напівпровідника.

Важлива перевага розподіленої моделі Лінвілла – можливість досить просто врахувати зовнішні впливи (фотоелектричні явища, вплив електро-магнітних полів, дії ядерної та космічної радіації тощо) шляхом додавання генераторів струму, що враховують відповідні явища.

Модель виходить у разі, якщо область бази уявити однією секцією моделі Лінвілла і знехтувати дрейфовими складовими струмів переходу. Для статичного режиму отримаємо розподіл струмів у базі (рис. 5, а).

Тут Iе, Iб, Iк – струми через виводи емітера, бази і колектора.

Електрони, що інжектуються емітером і колектором у базу, частково рекомбінуються в ній, утворюючи рекомбінаційні струми, а частково досягають протилежного переходу. Тут Inе, Inк – загальний електричний струм відповідно через емітерний і колекторний переходи.

Рекомбінація відбувається в усій області бази. Параметри і змінні усереднюються в межах секції, тому рекомбінаційний струм представляється у вигляді двох зосереджених складових Iрек.е і Iрек.к.

Струм переносу Iг= Inе – Iрек.е. Діркова складова емітерного дифузійного струму Iре не створює перенесення носіїв між емітером і колектором, оскільки для основних носіїв у базі р-типу переходи створюють потенційний бар’єр, що не пропускає дірки. Тому струм Iре повністю входить у струм бази.

Суму рекомбінаційного Iрек.е і діркового струму Iре позначимо Iед. Анало-гічно, Iкд – сума рекомбінаційного Iрек.к і діркового струму Iрк колекторного переходу в зоні бази.

Задачу отримання математичної моделі транзистора можна сформулювати таким чином: необхідно пов’язати струми Iг, Iед з напругами (щодо бази) на емітерному Uеб і колекторному Uкб переходах.

Представивши ці струми як залежні джерела, можна від розподілу струмів у базі перейти до початкового варіанта еквівалентної схеми.

Доповнивши статичну схему ємностями емітерного Се і колекторного Ск переходів, опорами витоку переходів Rуе, Rук і об’ємними опорами бази rб і колектора rк, отримаємо повну еквівалентну схему транзистора (рис. 7).

Залежності Iг, Iед і Iкд від Uеб і Uкб для статичного режиму визначаються шляхом аналітичного розв’язання основних рівнянь (32) у разі одно-вимірного наближення й усереднених значень параметрів напівпровідника.

Ці параметри, крім перелічених вище електрофізичних, містять площі емітерного SЕ і колекторного SK переходів. Остаточні вирази для джерел струму зображені на рисунку 5.

 

 

 

де І_ТЕ, І_ТK – відповідно теплові струми емітерного і колекторного переходів; mφ_ТЕ, mφ_ТK – температурні потенціали переходів; В, В₁ – коефіцієнти передачі струму бази відповідно в нормальному активному і в інверсному активному режимах.

Перелічені параметри називаються електричними параметрами моделі транзистора.

Рисунок 7 – Еквівалентна схема моделі транзистора

 

Інерційні властивості р-n-переходу пов’язані з тим, що в перехідних процесах, крім струму ІЕД(ІКД), через перехід повинен протікати струм, що забезпечує зміну заряду неосновних носіїв у базі й обумовлюється членом dn/dt у рівняннях безперервності, і струм, який забезпечує зміну просторового заряду іонізованих атомів домішок в області просторового заряду.

Першу складову можна відтворити за допомогою дифузійної ємності С_ДИФ, другу – бар’єрної ємності Сб. Аналітичне розв’язання рівняння безперервності в одновимірному наближенні дозволяє визначити С_ДИФ, а розв’язання рівняння Пуассона – Сб. Ці вирази для моделі транзистора на рисунку 5 мають вигляд:

 

 

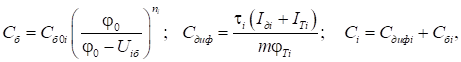
де I ϵ {e, к} – індекс; С_б0і – значення бар’єрної ємності за умови U_іб = 0; φ₀ – контактна різниця потенціалів; n_i – коефіцієнт ( n_i =0,5 для плавних переходів,   n_i = 1/3 для різких переходів); τ_i – постійна часу переходу.

Ці параметри доповнюють перелік електричних параметрів для моделі на рисунку 8. Еквівалентна схема моделі транзистора Еберса-Молла отримана аналогічно, на основі суперпозиції струмів для нормального й інверсного транзисторів, що працюють в активному режимі.

Для сучасних інтегральних транзисторів характерна асиметрична структура. Транзистори цього типу мають такі властивості: неоднорідну область бази (наявність градієнта концентрації домішок у ній); витіснення інжекції до периферії емітера; дуже незначний інверсний коефіцієнт підсилення; істотно різна площа емітерного й колекторного переходів; вплив підкладки на процеси в транзисторі; робота за умови високих рівнів інжекції, тобто необхідно враховувати дифузію і дрейф носіїв у базі.

Оригінальні моделі інтегральних транзисторів основані на обліку двовимірних і асиметричності транзисторної структури. Багатосекційні двовимірні моделі є найбільш точними, у них кожна секція заміщається відповідною еквівалентною схемою. Такі розподілені моделі складні за кількістю схемних компонентів і за кількістю параметрів. Виділимо такі зосереджені двовимірні моделі інтегрального транзистора: IBIS і BIRD. У них, поряд з електричними та електрофізичними параметрами, враховуються геометричні розміри топології і профіль розподілу домішки в транзисторі.

Модифікації моделі на рисунку 8 щодо інтегрального транзистора значно економічніші за оригінальні моделі. Вплив підкладки враховується шляхом введення в еквівалентну схему елементів паразитного р-n-р-транзистора (рис.6). У цій моделі струм неосновних носіїв, інжектованих у колектор колекторним переходом (передбачається, що перехід колектор-підкладка ізолюючий, тобто завжди закритий І'_r = B_П ‧І_КД), де B_П – коефіцієнт передачі струму паразитного р-n-р-транзистора. Ємність підкладки СП обчислюється за формулами, аналогічним С_к і С_е. Інші ефекти враховуються, як правило, шляхом апроксимації відповідних експериментальних залежностей.

На рисунку 9 показана типова залежність коефіцієнта посилення транзистора В від статичного струму емітера ІЕ. За умови апроксимації цієї залежності аргументом може бути струм моделі, але оскільки цей струм пропорційний величині е = exp(U_ЕБ / mφ_ТЕ – 1), то аргументом зручно використовувати е. Апроксимуючою функцією використовуються поліноми або експоненціальні функції, наприклад B = AeDexp(Се), де A, D, С – коефіцієнти апроксимації.

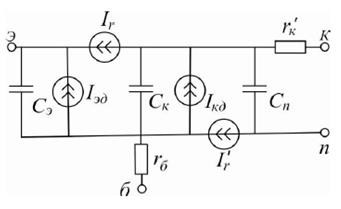
Рисунок 8 – Еквівалентна схема моделі інтегрального транзистора

 

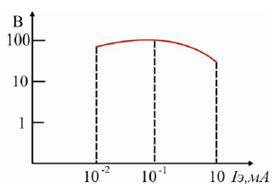
Рисунок 9 – Залежність коефіцієнта В від струму емітера

 

Багато додаткових ефектів можна врахувати шляхом додавання зовнішніх щодо вихідної моделі схемних елементів.

Передбачувані моделі зручні як складові в різних схемотехнічних розрахунках, особливо для створення інтегральних схем, коли неможливо розділити транзистор або напівпровідниковий діод і пасивний елемент – резистор чи ємність, які теж виконуються у вигляді p-n-переходу.

 

ТЕМА 3 СХЕМОТЕХНІЧНЕ МОДЕЛЮВАННЯ

1Формальне подання структури на макрорівні

Першим етапом моделювання об’єктів на макрорівні має бути заміна реального об’єкта деяким графічним поданням, що складається з пов’язаних між собою гілок, – графами та еквівалентними схемами.

Графи застосовуються не тільки для подання топологічних рівнянь у моделях макрорівня. Ними широко користуються для отримання структурних і функціональних математичних моделей на різних рівнях проектування, а також для вирішення завдань синтезу структури. Для представлення структур об’єктів у процесі їхнього моделювання застосовуються два різновиди графів: графи зв’язків і полюсні. Ці різновиди виражають одні й ті самі відомості про структуру об’єктів, але в різній формі. Хоча в конкретному завданні будь-яка одна з цих форм може виявитися більш наочною для користувача, у загальному випадку віддати перевагу тому чи іншому різновиду не можна. З огляду на те, що застосування обох різновидів приводить до ідентичних результатів, розглянемо та будемо використовувати тільки полюсні графи, як більш поширені.

Графом називають сукупність вершин (вузлів) і ребер (гілок). Визначення графа може бути записано в такому вигляді: Г (У, Р, І), де У – безліч вершин; Р – безліч ребер; І – інцидентор – покажчик способу, з’єднання ребер один з одним.

 

 

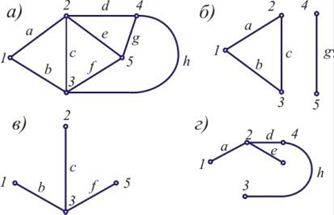
Рисунок 1 – Зв’язковий (а) і незв’язковий (б) графи, приклади дерев для зв’язкового графа (в, г)

 

Спрямований граф (орієнтований, або орграф) – граф, для ребер якого вказані певні напрямки. Ребра спрямованого графа називають дугами. На рисунку 1, а показаний граф, у якому безліч ребер Р є {а, b, c, д, e, f, g, h}, a безліч вершин  У = {1, 2, 3, 4, 5}. Підграфом називають таку частину графа, яка містить деякі вершини та ребра графа, зокрема серед ребер можуть бути тільки ті, які пов’язують вершини підграфа. Нехай на рисунку 1, а підграф є граф Г’ (У’, Р’, И’), і якщо У’ = {1, 2, 3}, то в підграф може мати тільки гілки а, b, с. Якщо підграф містить усі вершини графа, тобто У’=У, то підграф називають суграфом.

Маршрутом називають будь-яку послідовність s ребер, у якій сусідні ребра інцидентні одній і тій самій вершині. Термін «інцидентність» означає співвідношення об’єктів типу «проходить через ...» або «знаходиться на ...». На рис.1, а в графі послідовності (b, с, е, f, с, d) і (е, g) – маршрути, однак (а, h) маршрутом не є, оскільки ребра а та h інцидентні різним вершинам. Якщо в маршруті немає повторюваних ребер, то маршрут називають ланцюгом. Якщо ланцюг починається і завершується в одній і тій самій вершині, то маємо цикл – контур. Кількість ребер у s називають довжиною маршруту.

Зв’язковим графом називають граф, у якому можна вказати маршрут, що з’єднує будь-які вершини. Це визначення можна записати в такій формі: «якщо Ɐх, y ϵ Y(ⱻ S(x, y), то граф зв’язковий». Дослівно подібний запис читається так: «якщо для будь-яких вершин х і у, що належать безлічі Y, існує маршрут s, то граф зв’язний». Граф на рисунку 1, а – зв’язний. Прикладом незв’язного графа може бути граф на рисунку 1, б.

Деревом зв’язкового графа називають зв’язний підграф без циклів. Так, на рисунку 1, в, г наведено дерева для графа, зображеного на рисунку 1, а. Деревом, що покриває (фундаментальним) дерево (основу), називають зв’язним суграфом без циклів, тобто дерево є фундаментальним, якщо його гілки охоплюють всі вершини графа і не утворюють циклів. Гілками дерева називають ребра графа, що містяться в дереві, а хордами – ребра графа, що не увійшли в дерево. На рисунку 1, г зображено фундаментальне дерево. Для одного й того самого графа можна вказати кілька фундаментальних дерев, кожному вибору фундаментального дерева відповідає свій поділ безлічі ребер на підмножини гілок дерева В і хорд X. У разі дерева, показаного на рисунку 1, г, маємо В = {а, d, e, h} і    Х = {b, с, f, g}. Якщо позначити кількість ребер у графі через α, а кількість вершин – через β, то у фундаментальному дереві завжди буде β – 1 гілок і α – β + 1 хорд.

Контуром k-ї хорди називають безліч ребер, що утворюють цикл у графі, отриманому в разі додавання k-ї хорди до дерева. Наприклад, контуром хорди f для графа рисунку 1, а і дерева 1, г буде безліч ребер {f, е, d, h}.

Перетином гілки дерева називають безліч ребер, що перетинаються лінією перетину, якщо: а) серед гілок дерева перетинається єдина; б) лінія перетину замкнута і ребро може перетинатися не більше ніж один раз.

На графі рисунка 2, а дерево виділено жирними лініями; пунктирними тут показані лінії перетину: перетином гілки а буде безліч ребер {а, е}, перетином гілки b – безліч ребер {b, е, f} тощо.

 

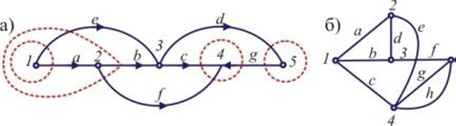
Риcунок 2 – Граф, його остов і лінії перетину гілок дерева (а); граф з матрицею суміжності (б)

 

За допомогою матриці інциденцій A = [a_ij] може бути виражена та сама інформація, яка міститься в графі. У цій матриці β – 1 рядків та α стовпців.

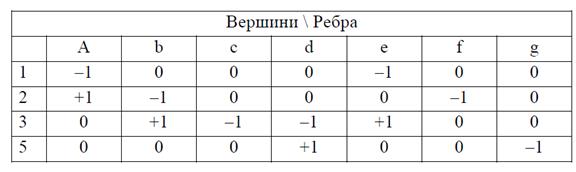
Кожному вузлу, за винятком одного, прийнятого за базовий, у матриці відповідає один рядок; кожному ребру – один стовпець. У стовпці записуються одиниці на перетині з рядками тих вузлів, яким ребро даного стовпчика. Якщо граф спрямований, то знаки одиниць вказують напрямки дуг: +1 відповідає рядку вузла, до якого направлено ребро, (–1) – рядку другого вузла. У решти клітинах матриці записуються нулі. Матриця інциденцій для графа рисунка 1, а в тому випадку, коли базовим вузлом є вузол 3, представлена в таблиці 1.

Граничні вершини ребра – вершини, інцидентні цьому ребру.  Кратні ребра – ребра з однаковими граничними вершинами. Мультиграф – графи, які мають кратні ребра. Степінь вершини – кількість ребер, інцидентних вершині. Дві вершини є суміжними, якщо вони з’єднані ребром.

Матрицею суміжності R, що відповідає графу Г, називають квадратну матрицю порядку п, де п – число вершин графа Г, у якій елемент r_ij дорівнює кількості ребер, з’єднують вершини з номерами i та j. Матриця суміжності містить повну інформацію про граф, і тому завдання ЕОМ деякого графа зазвичай зводиться до завдання матриці суміжності, що найчастіше здійснюється з урахуванням її розрідженості.

Таблиця 1 – Матриця інциденцій.

Графи – зручний засіб відображення структур проектованих об’єктів. Найчастіше в такому відображенні вершини графа ототожнюються з елементами структури, а ребра відповідають зв’язкам між елементами. У цьому випадку ребра графа ставлять відповідно до значення деякого параметра об’єкта, названого вагою.

 

Рисунок 3 – Ієрархічне дерево рішень

 

Значення ваги проставляють поруч з ребрами і граф називають зваженим графом. Так, у зображенні структури комплексу апаратури вершини можуть відтворювати пристрої, ребра відповідають зв’язкам між пристроями, а вагою може бути довжина зв’язків. Іноді, навпаки, ребрами зображують елементи, а вершинами – зв’язки між елементами. Таке уявлення структур частіше використовується в моделюванні об’єктів. Ієрархічні структури зручно зображувати у вигляді дерев, прикладом може бути дерево, показане на рисунку 3.3. Вершини таких дерев зазвичай поділяють на рівні (яруси). Так, на рисунку яруси відзначені римськими цифрами I–IV. Єдину вершину найвищого рівня називають кореневою вершиною (коренем).

Якщо граф відображає тільки такі структурні особливості, як спосіб зв’язку елементів один з одним, то еквівалентна схема містить повнішу інформацію про об’єкт: відображає також фізичну сутність окремих елементів. У загальному випадку для еквівалентних схем відсутня настільки ж чітка та однозначна система термінів і позначень, як для графів. У зображенні еквівалентних схем допускається використовувати багато позначень принципових схем.

Зображення гілок усіх можливих типів наведені на рисунку 4.

 

 

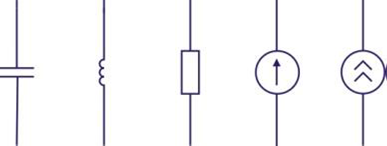
                                а)               б)                в)               г)               д)

Рисунок 4 – Типи гілок в еквівалентних схемах

 

Кожній гілці відповідає компонентне рівняння:

- для ємнісної гілки (рис. 3 а) – рівняння, що пов’язує I і dU / dt, зазвичай це рівняння вигляду I = C(dUldt), де I і U – фазові змінні типу струму і різниці потенціалів (напруги), де C – ємність;

- для індуктивної гілки (рис.3 б) – рівняння, що пов’язує U і dI/dt, зазвичай це рівняння вигляду U = L(dI/dt), де L – індуктивність;

- для резистивної гілки (рис. 4 в) – рівняння, що пов’язує U і I, звичайно це рівняння вигляду U = RI, де R – опір;

- для гілки джерела напруги (рис. 4 г) – рівняння, що пов’язує напругу U зі змінною t і, можливо, із фазовими змінними інших гілок: U = f₁(t, V); де V – вектор фазових змінних; t – час; в окремому випадку, можливо, U =     = const.

- для гілки джерела потоку (рис. 4 д) – рівняння, що пов’язує струм I з часом t і, можливо, з вектором V, має вигляд: I = f₂(t, V) ;  можливо, I = const.

Залежна гілка – гілка, параметр якої (U в джерелі напруги, I в джерелі струму, або С, L, R) залежить від будь-яких фазових змінних.

Як уже зазначалося, кожному вузлу схеми відповідає певне значення фазової змінної типу потенціалу; кожній гілці – значення змінних I і U, що фігурують у компонентних рівняннях. З’єднання гілок один з одним, тобто створення вузлів, має відображати взаємодію елементів у системі.

 

2 Форми подання моделей елементів схем

Особливість математичного забезпечення схемотехнічного проектування полягає в моделюванні елементів електронних схем і аналізі конкретних типів проектованих схем.

У моделюванні компонентами електронної схеми є резистор, конденсатор, котушка індуктивності, окремий електронний прилад у дискретному або інтегральному виконанні, джерело струму або напруги тощо.

Елементом електронної схеми може бути як компонент, так і типовий фрагмент схеми (вентиль, тригер тощо). Математична модель електронної схеми в аналізі на ЕОМ – система звичайних диференціальних рівнянь, що пов’язує струми й напруги в різних компонентах схеми.

Математична модель схеми (ММС), отримана безпосереднім об’єднанням моделей компонентів у загальну систему рівнянь на основі топологічних рівнянь, називається повною моделлю схеми. ММС, що є простіша за витратами часу і пам’яті ЕОМ на її реалізацію, ніж повна модель, називається макромоделлю схеми.

Типові фрагменти схеми (функціональні вузли) складаються з окремих компонентів, тому моделі таких фрагментів у складі складних електронних схем є макромоделі.

Отже, можна виділити два основних типи моделей елементів електронних схем: моделі компонентів і макромоделі функціональних вузлів.

Математична модель елемента електронної схеми є системою ЗДР щодо фазових змінних: струму I та напруги U. Існує декілька форм подання такої моделі: інваріантна, схемна й алгоритмічна (або програмна).

Інваріантна форма – це запис системи ЗДР безвідносно до методу її чисельного рішення. Систему ЗДР можна отримати в нормальній формі Коші або у вигляді системи алгебродиференціальних рівнянь.

Недолік інваріантної форми – це відсутність наочності в синтезі структури моделі та складність включення моделі елемента в бібліотеку моделей конкретної програми аналізу електронних схем, оскільки виникають труднощі з поданням системи рівнянь графом для формування ММС.

Схемна форма – представлення моделі елемента у вигляді еквівалентної електричної схеми, що складається з певного набору електричних компонентів і зв’язків між ними. Еквівалентні схеми розрізняють залежно від складу допустимих компонентів.

 

 

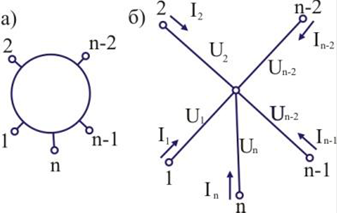
Рисунок 5 – Багатополюсник (а) та його полюсний граф (б)

 

Базові еквівалентні схеми складаються з таких двополюсників: ємності С, індуктивності L, резистора R, джерела струму I (постійний або залежний від фазових змінних і часу) і напруги Е (постійна або залежна від фазових змінних і часу). Базові еквівалентні схеми відповідають вимогам, що висуваються за умови синтезу структури моделі та включення її в бібліотеку моделей елементів електронних схем. Недолік таких схем – у моделюванні складних функціональних вузлів. Вони втрачають свою наочність, стають громіздкими і незручними, тому використовуються здебільшого в моделюванні компонентів електронних схем.

Узагальнені еквівалентні схеми допускають використання, крім перелічених двополюсників, довільних багатополюсних елементів. Кожен двополюсний компонент характеризується струмом, що протікає через нього, і напругою між його полюсами. У багатополюсному елементі один з полюсів приймається за базисний, щодо якого визначаються напруги інших полюсів. Нехай кількість полюсів багатополюсника n і вузол з номером n – базисний. Кожен полюс характеризується струмом, що впадає до нього, та напругою щодо базисного вузла Uin (для базисного вузла U_nn = 0, ), які створюють два вектори невідомих Iм і Uм, обидва розмірністю п. За цих умов багатополюсник можна розглядати як сукупність п двополюсників (рис. 5), тому його нарівні з іншими двополюсниками можна включити до узагальненої еквівалентної схеми для формування ММС. Математична модель багатополюсника має вигляд

 

 

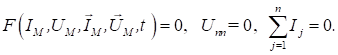
Отже, за допомогою багатополюсника можна уявити будь-який функціональний вузол електронної схеми. Приклади багатополюсників: трансформатор, мікросхеми з великою кількістю виводів тощо. Узагальнені еквівалентні схеми застосовуються для отримання макромоделей.

Алгоритмічна (програмна) форма – це програма обчислення усіх необхідних функцій і коефіцієнтів конкретної моделі елемента в разі її включення в бібліотеку моделей програми аналізу електронної схеми. Структура алгоритму моделі залежить від методу формування ММС, закладеного в конкретну програму аналізу. Наприклад, для методу вузлових потенціалів необхідно обчислити вектор вузлових струмів і матрицю вузлових провідностей для еквівалентної схеми моделі в певний момент часу. Розглянемо отримання програми моделі напівпровідникового діода для узагальненого методу формування ММС. Модель діода має вигляд:

 

 

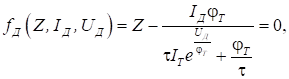
де I_Д  – струм діода; U_Д – напруга на діоді; Z = dU_Д /dt; φ_T , τ, I_Т  – параметри діода.

Для узагальненого методу формування ММС у програмі моделі елемента мають бути обчислені вектор нев’язок Q для рівнянь моделі в разі заданих значень фазових змінних і матриця А приватних похідних вектор-функції рівнянь моделі по фазових змінних. Модель діода має одне рівняння і три змінних, тому розмір матриці частинних похідних (1,4). Алгоритм для складання програми моделі діода:

1.   Описати змінні та постійні величини: q, Z, τ, I_Т, матрицю А(1,4).

2.   Визначити

3.   Розрахувати а₁₁ = ∂f_Д/∂Z; а₁₂ = ∂f_Д/∂I_Д; а₁₂ = ∂f_Д/∂U_Д;

Моделі елементів для узагальненого методу формування ММС не залежить від методів інтегрування систем ЗДР, оскільки в них не потрібна заміна похідних Z різницевими формулами, як у методі вузлових потенціалів.

 

3 Моделі компонентів електронних схем. Макромоделі в електроніці

Похибки моделювання електронних схем визначаються наближеністю моделей компонентів схеми, методів чисельного розв’язання і неточністю завдання вихідних даних (параметрів моделей компонентів, зовнішніх параметрів та ін.).

Чисельні методи в програмах аналізу електронних схем здебільшого забезпечують порівняно високу точність розрахунку. Значну похибку в остаточні результати вносять помилково задані внутрішні та зовнішні параметри схеми, але ця похибка усунена, оскільки помилки вихідних даних можна виправити. Похибки конкретних моделей компонентів схеми не можна виправити інакше, ніж заміною на більш точну. У разі низької точності моделей транзисторів, діодів, резисторів застосування програм аналізу схем у багатьох випадках буде неефективним. З іншого боку, з урахуванням усіх складових загальної похибки моделювання застосування окремих високоточних моделей компонентів призведе до нераціональних витрат часу і пам’яті ЕОМ. 

Теоретичний підхід характеризується тим, що всі рівняння моделі виводяться з фізичних особливостей процесів у компоненті. Цей підхід забезпечує отримання найбільш точних і універсальних моделей.

Експериментальний (емпіричний) підхід оснований на експериментальному дослідженні зв’язків між струмами і напругами на зовнішніх виводах компонента. Рівняння моделі отримуються шляхом апроксимації експериментальних характеристик відповідними функціями. Такі моделі точні тільки для умов, у яких проводилися вимірювання, і відображають виміряні залежності, тому не універсальні.

Експериментально-теоретичний підхід оснований на поєднанні попередніх. Наприклад, вид формульних залежностей спочатку отримується з фізичних міркувань, потім ці залежності коригуються, виходячи з результатів експерименту.

Вихідною інформацією для отримання макромоделей є повні моделі вузлів на рівні моделей компонентів. Тому основне теоретичне завдання макро-моделювання полягає у створенні формальної методики, що дозволяє отримати необхідну макромодель з повною моделі. У загальному випадку для нелінійних динамічних схем таке завдання не вирішене, зокрема найбільш складний синтез структури макромоделей. Макромоделі другого рівня відображають основні вихідні схемотехнічні параметри вузла. Приклад моделі транзистора показано на рисунку 6.

 

Рисунок 6 – Модель транзистора

 

Макромоделі третього рівня відображають додаткові схемотехнічні та технологічні особливості функціонального вузла (різні паразитні ефекти, неідеальність основних характеристик тощо). Ці параметри визначаються шляхом аналізу функціонального вузла за допомогою повної моделі.

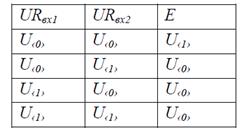
Синтез макромоделей першого рівня складності простий і виконується за допомогою формальних або базових еквівалентних схем. Еквівалентна схема макромоделі логічного елемента І–НЕ (рис. 6), побудована на основі ідеального вхідного (R_ВХ → ∞)   і вихідного (R_ВИХ → 0) опорів і залежного джерела Е, реалізує логічну функцію елемента згідно з таблиці 1. Тут використовуються такі позначення: U_RBX1, U_RBX2 – напруги на відповідних опорах; U_«0», U_«1» – рівні логічного нуля й одиниці відповідно.

На рисунках 7, 8 показані еквівалентні схемі елемента І-НІ та макромоделі ідеального операційного підсилювача з коефіцієнтом підсилення К. Макромоделі другого та третього рівнів складності розробляються двома способами: на основі блокового макромоделювання шляхом поступового ускладнення простих еквівалентних схем, починаючи з макромоделей першого рівня; спрощенням вихідної повної моделі вузла до рівня, що визначається необхідною точністю моделювання його зовнішніх характеристик з точки зору функціонування всього електронного пристрою. З точки зору формалізації синтезу макромоделей перший підхід більш перспективний.

Таблиця 1 – Дані для побудови еквівалентної схеми макромоделі логічного елемента І-НЕ

Блоковий метод макромоделювання оснований на створенні набору еквівалентних схем типових блоків, з яких у подальшому можна складати різні макромоделі. Типові блоки можна поділити на два класи: універсальні макроелементи та типові базові елементи. Універсальні макроелементи реалізують математичні описи основних властивостей електронних пристроїв і не мають фізичного прототипу (опис логічних рівнянь, типових характеристик, фіксація моменту досягнення порогу спрацьовування тощо). Дуже складно розробити функціонально повний набір макроелементів для оперативного макромоделювання цифрових і аналогових схем. Набір макроелементів дозволить формалізувати розробку макромоделей другого рівня складності.

Типові базові елементи відображають типові структурні частини модельованих вузлів (вхідні, проміжні та вихідні каскади схем тощо). У першому наближенні базові елементи мають бути «ідеальними каскадами» електронних схем за умови мінімальної складності їхньої структури. Набір моделей базових елементів у поєднанні з макроелементами дозволить формалізувати розробку найбільш точних макромоделей третього рівня складності.

 

           Рисунок 7 – Макромодель                  Рисунок 8 – Макромодель

                      елемента І-НЕ                              операційного підсилювача

 

На рисунку 9 наведена еквівалентна схема макромоделі третього рівня для операційного підсилювача 130УД7.

 

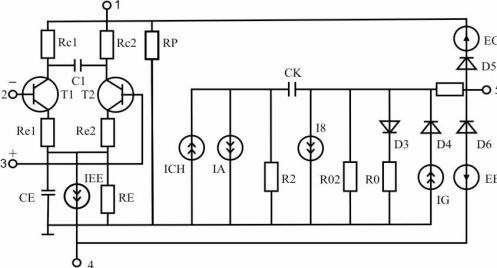
Рисунок 9 – Макромодель мікросхеми 130УД7: 2 ... 7 – виводи мікросхеми

 

Каскади «вхідний диференційний» і «вихідний диференційний» моделюються за допомогою базових елементів, а проміжний – за допомогою макроелементів.

 

 

4 Ідентифікація параметрів моделей елементів електронних схем

Основні способи визначення параметрів моделей елементів – розрахунковий і експериментальний.

Розрахунковий метод ґрунтується на безпосередньому розрахунку пара-метрів за відомими аналітичними формулами та виразами. Наприклад, параметри моделі транзистора розраховуються на основі електрофізичних параметрів напівпровідника і даних про геометричні розміри топології транзистора. Параметри макромоделей розраховуються на базі аналітичних методів розрахунку модельованих функціональних вузлів.

Експериментальний метод передбачає проведення серії експериментів (натурних, машинних) для визначення параметрів моделі елемента. Експерименти бувають двох типів, коли визначаються внутрішні параметри моделі елемента безпосередньо (прямо) або вихідні параметри елемента, що моделюється з метою подальшого розрахунку внутрішніх параметрів його моделі оптимізаційними методами.

У разі прямого виміру параметри моделі визначаються у встановлених для даного елемента режимах. Методики визначення параметрів моделі різні, тому вимір кожного з них здійснюється за своєю власною схемою і потребує своєї вимірювальної апаратури. За умови великого числа параметрів процес вимірювань є тривалою та трудомісткою процедурою. У разі оптимізаційних методів для визначення параметрів моделей потрібна розробка відповідного програмного забезпечення. На підставі виміряних еталонних вихідних параметрів елемента за допомогою цих програм визначаються значення внутрішніх параметрів досліджуваної моделі елемента, які забезпечують най-кращий збіг результатів моделювання з еталонними вихідними параметрами.

Для макромоделей вихідні параметри вузла, як правило, розраховуються на ЕОМ за допомогою повної моделі. Наскрізне, автоматизоване проектування обчислювальної апаратури приводить до поступової відмови від визначення параметрів моделей безпосереднім вимірюванням на реальних об’єктах, тим більше що в процесі проектування часто відсутній реальний прототип елемента, який моделюється. Для ідентифікації параметрів елементів більш перспективне визначення вихідних параметрів елемента (або безпосередньо параметрів моделі) за допомогою більш точних моделей цього елемента на інших рівнях проектування. Наприклад, параметри схемної моделі транзистора можна визначити за допомогою його фізико-топологічних моделей.

Розробка надійних в експлуатації програм ідентифікації параметрів моделей елементів – складне й трудомістке завдання. Особливу складність має розробка оптимізаційних методів, оскільки оптимізація проводиться в просторі багатьох змінних, а цільова функція не має аналітичного уявлення. Як цільова функція зазвичай використовується відхилення вихідних характеристик елемента від еталонних у робочому діапазоні зовнішніх впливів. Найбільш часто мінімізується середньоквадратичне відносне відхилення:

 

                                   

 

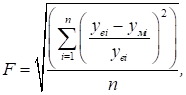
де y_еі, у_мі – відповідно еталонне й отримане на моделі значення i-гo вихідного параметра елемента; n – кількість вихідних параметрів.

Правильне визначення параметрів моделей елементів має дуже велике значення у вирішенні основних завдань схемотехнічного проектування. Тому впровадження програм схемотехнічного проектування має супроводжуватися розробкою заходів щодо ідентифікації параметрів моделей елементів електронних схем, зокрема створення спеціального програмного забезпечення.

 

ТЕМА 4 МОДЕЛЮВАННЯ ЦИФРОВИХ ТА ЦИФРО-АНАЛОГОВИХ СХЕМ

1 Загальні положення

Основним видом аналізу цифрових і цифро-аналогових електронних схем є аналіз у часовій області. Математичну модель схеми отримуємо за допомогою універсальних методів формування ММС у вигляді нелінійної системи ЗДР:

 

                                              (1)

 

Завдання аналізу цифрових схем пов’язані з дослідженням схем невисокого ступеня складності (до 100 транзисторів) – цифрових мікросхем малого ступеня інтеграції, фрагментів ВІС тощо і складних схем ВІС з урахуванням розподілених параметрів електричних ланцюгів, що пов’язують фрагменти ВІС між собою. Основним методом аналізу в першому випадку є чисельне розв’язання системи (1) на заданому інтервалі часу за умови заданого набору вхідних імпульсів або рівнів напруги.

Зазвичай використовуються неявні методи інтегрування невисокого порядку точності з перемінним кроком. У процесі інтегрування розраховуються вихідні статичні та динамічні параметри – функціонали, що характеризують цифрові схеми: рівні логічної «1» і «0», часи затримань і тривалості фронтів вихідних сигналів та ін. У другому випадку необхідна розробка спеціальних швидкодіючих алгоритмів аналізу ВІС.

Труднощі аналізу ВІС пояснюються такими причинами: 1) розмірність системи (1) становить сотні й тисячі рівнянь навіть у використанні макромоделей, що призводить до великих витрат машинного часу; 2) для розрахунку характеристик ВІС необхідне моделювання десятків тактів роботи для різних сполучень вхідних сигналів, що призводить до збільшення тимчасового інтервалу моделювання; 3) необхідно враховувати розподілений характер міжз’єднань і компонентів ВІС і вплив теплових процесів на електричні параметри схем.

Для розробки алгоритмів аналізу ВІС застосовуються діакоптичні методи та змішане (багаторівневе) моделювання ВІС.

Діакоптичні методи (розбиття, декомпозиції) основані на поділі складної схеми (або системи рівнянь) на прості підсхеми (підсистеми) з урахуванням зв’язків між ними. Розв’язання задачі високої розмірності зводиться до послідовного (або паралельного) розв’язанням декількох підзадач меншої розмірності. Кожну подсхему можна, у свою чергу, розбити на більш прості підсхеми.

Поділ складної схеми на підсхеми найчастіше виконується проектуваль-ником з урахуванням функціональної закінченості підсхем та їхньої повторюва-ності в структурі схеми. У деяких випадках розробляються спеціальні алгоритми розбиття графа схеми на слабкозв’язані між собою підграфи (кластери), які утворюють відповідні підсхеми. Після поділу схеми фазові змінні поділяються на внутрішні змінні окремих підсхем і граничні, що відображають зв’язки між підсхемами. Діакоптичні методи аналізу ВІС поділяються на три групи: підсхем, роздільного ітерування й роздільного інтегрування.

Методи підсхем характеризуються тим, що на етапі формування ММС спочатку групуються рівняння окремих підсхем, а в кінці – усі граничні рівняння. Унаслідок цього матриця Якобі системи (1) набуває форми блоководіагональної матриці з обрамленням.

Метод роздільного ітерування оснований на використанні різної швидкості збіжності ітерацій у вирішенні нелінійних алгебраїчних рівнянь для окремих підсхем.

Застосування методу Ньютона на кожному кроці інтегрування системи (1) приводить до однакового числа ітерацій для всіх підсхем, яке визначається за підсхемою з найбільш повільної збіжності ітерацій. У складній ВІС, як правило, метод Ньютона для кожної підсхеми збігається за різною кількістю ітерацій.

Незалежне розв’язання системи нелінійного алгебраїчного рівняння (НАР) для кожної підсхеми значно знижує обчислювальні витрати під час аналізу всієї ВІС. Розглянемо можливий алгоритм роздільного ітерування системи НАР в процесі аналізу ВІС. Кожній підсхемі відповідає своя підсистема НАР:

 

                                    (2)

 

де V_i  – вектор внутрішніх змінних i-ї підсхеми; V_ri  ϵ V_r  – вектор граничних змінних.

Система граничних рівнянь

F_r(V, V_r) = 0,                                                   (3)

 

де V – вектор, що складається з підвектора V_i.

Кожна система (3) розв’язується методом Ньютона автономно щодо Vi за умови фіксованого вектора V_ri,k, де k – номер ітерації Ньютона у розв’язанні системи (3). Потім виконується (k+1)-я ітерація для розв’язання системи (3) у разі фіксованого вектора V. Закінчення ітераційного процесу визначається заданою точністю рішення системи (3). Збіжність у розв’язанні систем (2) від ітерації до ітерації поліпшується за умови збіжності розв’язання системи (3). Якщо V_ri,k+1 = V_ri,k, то систему (2) для i-ї підсхеми на (k+1)-ї ітерації розв’язувати не потрібно.

Методи роздільного інтегрування основані на різній інерційності окремих підсхем, коли в одній підсхемі перехідні процеси протікають швидко, а в іншій – повільно. До методів роздільного інтегрування належать методи вкладених кроків, багатополюсних підсхем, односпрямованих реакцій, прогнозованих реакцій, релаксації форми сигналу (РФС).

Розглянемо найбільш відомий метод багатополюсних підсхем, оснований на автономному інтегруванні рівнянь усіх підсхем зі своїм оптимальним кроком за умови фіксованих значень граничних змінних. Кожній підсхемі відповідає своя підсистема ЗДР:

 

                            (4)

 

Система граничних ЗДР має вигляд:

 

                                       (5)

 

На кожному кроці інтегрування системи (5) виконуються такі операції: прогнозування граничних змінних і , автономне інтегрування систем (4) у межах кроку за умови фіксованих значень V_{ri пр} і V′_{r пр}, обчислення остаточних значень граничних змінних V_r на даному етапі й корекції внутрішніх змінних за допомогою відомих коефіцієнтів чутливості. У разі автономного інтегрування необхідно визначити коефіцієнти чутливості внутрішніх змінних до змін граничних змінних, які використовуються для формування матриці Якобі в остаточному розв’язанні системи (5) і корекції внутрішніх змінних з урахуванням остаточних значень. Це завдання вирішується шляхом інтегрування одночасно із системою (5) лінійної пов’язаної системи ЗДР.

Отже, діакоптичні методи забезпечують прискорений аналіз ВІС шляхом зведення задачі великої розмірності до сукупності підзадач меншої розмірності. Організація автономних обчислювальних процесів для підсхем дозволяє проводити аналіз ВІС за умови обмеженого обсягу оперативної пам’яті ЕОМ і виконувати паралельні обчислення в багатопроцесорних обчислювальних системах.

Змішане багаторівневе моделювання основане на паралельному використанні моделей і алгоритмів різних рівнів у процесі розрахунку. Багаторівневе моделювання дозволяє описувати різні частини схеми ВІС з різним ступенем деталізації. Основні рівні деталізації – функціонально-логічний, схемотехнічний, приладовий. Змішане моделювання дозволяє автоматизувати схемотехнічне проектування цифрових і цифро-аналогових електронних схем. В алгоритмах змішаного (багаторівневого) моделювання модель ВІС може одночасно містити моделі елементів і підсхем на всіх рівнях деталізації, тому інформаційне узгодження рівнів є одним з основних завдань. У вирішенні цього завдання можна виокремити два підходи.

Аналіз ВІС виконується на схемотехнічному рівні, а моделі підсхем на інших рівнях надаються відповідними макромоделями. Приклади таких макромоделей: багатосекційна Лінвілла для транзистора відбиває процеси в транзисторі на мікрорівні (щодо фізико-топологічних моделей транзистора ця модель буде макромоделлю); макромодель логічного елемента І–НЕ відбиває логічну функцію для цього елемента. Такий підхід у поєднанні з діакоптичними методами дозволяє вирішувати багато завдань аналізу (зокрема облік міжз’єднань і теплових процесів) й оптимізації електричних схем ВІС. Але підхід не завжди ефективний, особливо в моделюванні НВІС.

Це пов’язано з тим, що в разі отримання макромоделей мікрорівня відбувається втрата точності (за рахунок переходу від розподілених моделей до зосереджених), а для макромоделей системного рівня – втрата економічності (оскільки логічні елементи описуються на електричному рівні). У процесі аналізу кожна виділена підсхема ВІС моделюється і розраховується методами одного з перелічених вище рівнів, які користувачі обирають залежно від конкретних вимог до точності та економічності моделі підсхеми.

Спільний аналіз схеми ВІС виконується синхронно для всіх підсхем, водночас на стиках різних рівнів працюють спеціальні елементи-перетворювачі фазових змінних для організації зв’язків між різнорівневими моделями. Розглянемо цей універсальний підхід докладніше, оскільки він забезпечує вдалий компроміс між вимогами точності (завдяки поданням найбільш відповідальних підсхем ВІС з потрібним ступенем деталізації) і економічності (завдяки поданням інших підсхем на більш високих рівнях моделювання аж до системного). На рисунку 1 показана можлива структура програмного забезпечення системи змішаного (багаторівневого) моделювання ВІС. Програми аналізу розподілених моделей забезпечують моделювання і розрахунок на мікрорівні активних і пасивних елементів ВІС, міжз’єднань і паразитних зв’язків, теплових ефектів. Програми аналізу електронних схем дозволяють проводити електричний розрахунок схем на рівні зосереджених моделей і макромоделей. Програми структурного і функціонально-логічного аналізу забезпечують проектування архітектури й логічних схем цифрових і цифро-аналогових ВІС. Усі ці підсистеми можуть працювати автономно для вирішення завдань проектування і спільно в процесі аналізу ВІС.

Зв’язок підсистем за інформацією здійснюється через загальну базу даних системи й елементи-перетворювачі інформації. Зв’язок підсистем з управління здійснюється за допомогою спеціальної програми-диспетчера, виконує такі функції: введення опису ВІС і звернення до трансляторів відповідних підсистем для формування моделей окремих підсхем; підключення між моделями різних рівнів елементів-перетворювачів інформації; формування повної ММС ВІС; вибір оптимальної послідовності звернень до різних моделей елементів у процесі розрахунку; синхронізацію роботи різних підсистем у ході розрахунку; зв’язок з іншими підсистемами САПР (наприклад, з підсистемою топологічного проектування ВІС та ін.).

Елементи-перетворювачі інформації перетворять дискретні сигнали в безперервні й навпаки. В асинхронному двозначному логічному моделюванні кожен сигнал має два можливих значення – «0» і «1», а час квантований за моментами перемикання сигналів. Перетворення безперервного сигналу в дискретний здійснюється за допомогою порогових функцій, тобто за умови напруги входу Uвх, меншій за деякий поріг Uпоp, логічний стан входу Q_BX = «0», якщо Uвх>Uпор, стан входу QBX = «1».

 

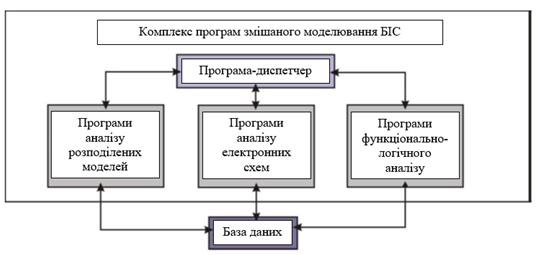
Рисунок 1 – Структура комплексу програм змішаного моделювання ВІС

 

Момент перетину пороговї напруги відповідає моменту появи сигналу. У разі зворотного перетворення слід уникати миттєвих перепадів напруги на виходах елементів-перетворювачів дискретних сигналів у безперервні, це може порушити стійкість обчислювального процесу в безперервній підсистемі.

Тому треба імітувати кінцевий час наростання логічних сигналів на виході елементів-перетворювачів. У низці випадків бажано відображати вхідні й вихідні вольт-амперні характеристики логічних елементів. Синхронізувати підсистеми можна на основі подієвого моделювання, за допомогою графа, що відображає напрямки потоків інформації, якими обмінюються моделі елементів.

Наприклад, у логіко-електричному моделюванні спочатку виконується крок інтегрування в електричній підсистемі, потім відбувається звернення до підсистеми логічного моделювання. Якщо в межах кроку з’являються нові події на вході електричної частини, то крок потрібно зменшити до появи першої нової події. Величина наступного кроку повинна вибиратися таким чином, щоб не перевищувати моменту появи черговї події на вході електричної частини схеми. Така організація обчислень пов’язана з тим, що події порушують гладкість безперервних змінних за часом. Подієве моделювання реалізується також урахуванням латентності.

Підсхема вважається латентною, якщо на поточному інтервалі часу (у межах кроку інтегрування) усі внутрішні та граничні змінні підсхеми не змінюються. Поки підсхема латентна, можна не розв’язувати рівняння, що слугують для визначення її внутрішніх змінних. Електрична підсхема латентна, якщо збільшення кожної змінної її похідної за часом не перевищує деяких заданих порогових значень в межах кроку. Логічна підсхема латентна в разі відсутності сигналів на входах і виходах.

Вибір порогових значень для електричних підсхем є складним завданням, оскільки маленький поріг не дає виграшу (якщо поріг дорівнює нулю, то підсхема ніколи не буде латентною), а великий – може призвести до помилкових результатів. Визначення латентності логічних підсхем технічно не створює труднощів. Тому доцільно враховувати латентності тільки для логічних підсхем, а для електричних підсхем виконувати інтегрування зі своїм оптимальним кроком.

 

2 Аналогові схеми

Аналогові електронні схеми поділяються на лінійні та нелінійні. Характеристики елементів електронних схем найчастіше нелінійні, тому під лінійними аналоговими маються на увазі схеми в прийнятті допущення про лінійності співвідношень між їхніми фазовими змінними в межах змін амплітуд вхідних сигналів. Такі схеми іноді називають малосигнальні (підсилювачі, фільтри та ін.). У режимі великих сигналів і під час обліку нелінійностей елементів схеми в робочих режимах аналогові схеми вважаються нелінійними (детектори, модулятори, автогенератори гармонійних коливань тощо).

Аналіз у частотній області – основний вид аналізу аналогових лінійних схем. У схемі визначаються струми і напруги як функції частоти. Вихідну математичну модель можна отримати за допомогою універсальних методів формування ММС у вигляді лінійної системи ЗДР: GV + WV = Q; де G, W – постійні матриці; V – вектор фазових змінних схеми; Q – вектор із постійними елементами та залежними від часу вхідними впливами.

За допомогою математичних перетворень Лапласа або Фур’є розв’язання цієї системи переводяться в область змінної p = σ + jω, яка називається комплексною частотою. Основна мета перетворень – зведення диференціальних рівнянь до алгебраїчних щодо комплексної частоти р. Унаслідок отримуємо модель схеми у вигляді системи лінійних алгебраїчних рівнянь:

 

AV ^′ = B,                                                       (6)

 

де А = pG + W;   V ^′= V(p);    B = Q′ + GV₀; Q′ = Q(p); V₀ – вектор початкових умов.

 

В аналізі лінійних схем інтерес мають відношення фазових змінних, взяті на окремо виділених гілках, відповідних входах і виходах схеми. У разі декількох вхідних джерел вихідну змінну визначають відповідно до принципу суперпозиції – як суму впливів кожного із джерел. Фазовими змінними в схемі є струми і напруги, тому співвідношення між вхідним джерелом і виходом схеми можна представити у вигляді чотириполюсника (рис. 2).

 

 

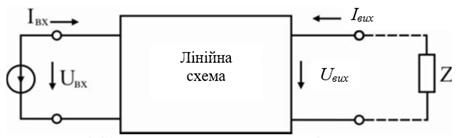
Рисунок 2 – Модель лінійної аналогової схеми у вигляді чотириполюсника

 

Представляючи кожну змінну у вигляді суми дійсної та уявної частини, тобто замінюючи р на σ + jω, можна отримати дві системи лінійних алгебраїчних рівнянь (ЛАР) для дійсної та уявної частини вектора V за умови частоти ω. Розв’язання цих систем дає модуль і аргумент для всіх змінних схеми на заданій частоті ω.

Відношення між струмами і напругами на сторонах чотириполюсника в операторній формі називаються схемними функціями, наприклад, коефіцієнт передачі напруги    К_U = UВИХ / UВХ, вхідний опір Z_ВХ = U_ВХ / I_ВХ  тощо. За умови переходу в частотну область значення модуля та аргументу комплексних схемних функцій у діапазоні частот визначають амплітудно-частотні (АЧХ) і фазочастотні характеристики (ФЧХ) схеми.

Методи частотного аналізу лінійних схем поділяються на дві групи: символічні та чисельні. Символічні методи основані на отриманні виразів для схемних функцій як раціональних функцій комплексної частоти з числовими коефіцієнтами. Наприклад, коефіцієнт передачі напруги

 

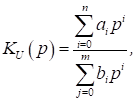                                         (7)

 

де ai і bi – коефіцієнти, що залежать від параметрів елементів схеми; m і n не перевищують кількості реактивних елементів у схемі.

Останній вираз отримано внаслідок застосування формули Крамера до системи (1). Символічні методи характеризуються швидким зростанням обсягу обчислень у разі збільшення розмірності задачі. Розширення меж складності аналізованих схем можливе на основі діакоптичних методів.

Чисельні методи основані на багаторазовому розв’язанні системи (2) для заданого набору точок на осі частот і отриманні АЧХ і ФЧХ схеми. Для обчислення АЧХ і ФЧХ необхідно задати точки в необхідному діапазоні частот. Для простих характеристик точки вибираються з рівномірним кроком за частотою, кількість точок 30 ... 100 на весь діапазон. У більш складних випадках потрібний змінний крок за частотою. Чисельні методи набули найбільшого поширення в частотному аналізі лінійних схем.

Аналіз лінійних схем у часовій області виконується для двох видів вхідних впливів: 1) стандартних імпульсних сигналів θ(t) – одиничної функції Хевісайда і δ(t)-дельта-функції Дірака; 2) вхідних сигналів довільної форми.

У разі впливу стандартних сигналів можна отримати аналітичний розв’язок вихідної лінійної системи ЗДР і визначити відповідно перехідну h(t)і імпульсну g(t) характеристики схеми. У цьому випадку доводиться розв’язувати складну задачу обчислення всіх власних значень і векторів матриці Якобі вихідної системи. За умови впливу сигналів довільної форми обчислюються перехідні процеси за частотними характеристиками схеми на основі кусково-лінійної або сплайнової апроксимації АЧХ і ФЧХ. У цьому випадку точність розрахунку перехідних процесів невисока. У загальному випадку для будь-яких вхідних сигналів основним методом аналізу лінійних схем у тимчасовій області є чисельне розв’язання вихідної системи на заданому інтервалі часу. У цьому разі зазвичай використовуються неявні методи інтегрування зі змінним кроком. Є широкий клас лінійних схем, відповідних резонансних пристроїв високої добротності (наприклад, фільтри зосередженої селекції). Час установлення стаціонарного режиму в таких схемах може містити тисячі періодів власних коливань. У цьому випадку звичайні методи інтегрування незастосовні через значну кількість кроків і накопичення великих методичних помилок. Для таких схем необхідно застосовувати спеціальні алгоритми чисельного аналізу.

Аналіз нелінійних аналогових схем у часовій області передбачає розгляд стаціонарних режимів коливань і перехідних процесів. Математичною моделлю схеми є система нелінійних ЗДР вигляду

V ^′= F(V, t),        V(t₀) = V₀.                                      (8)

 

Припустимо, що розв’язання системи можна апроксимувати виразом

 

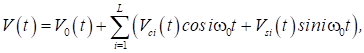                   (9)

 

де iω₀ – частоти гармонійних складових; ω₀ = 2π/Т; V_cі (t) та V_Si (t) – функції часу, що змінюються в загальному випадку набагато повільніше, ніж sinω₀t  і  cosω₀t, тобто порядок величин V_cі (t) і V_Si (t) набагато менший, ніж ω₀.

Стаціонарному режиму коливань відповідає періодичний розв’язок системи (9), якщо t →∞:

 

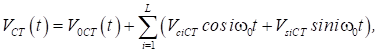                 (10)

Метод Ейпріла–Тріка для розв’язання цієї задачі оснований на визначенні вектора початкових умов V0, для якого справедлива рівність

 

V₀ = V(t₀) = V(t₀ + Т₀).                               (11)

 

Рівність (11) можна записати у вигляді

 

Ф(V₀)  = V₀ – V (t₀ + Т₀).                            (12)

 

Система (10) розв’язується методом Ньютона щодо V0. Для обчислення вектор-функції Ф(V0) для деякого значення V₀ необхідно проінтегрувати систему (9) на інтервалі [t₀, t₀ + Т₀].

Тому для обчислення матриці Якобі системи (9) [дФ/дV₀] застосовуються метод збільшень або варіаційні методи. В обох випадках обчислення матриці [дФ/дV₀] пов’язане із значними витратами машинного часу.

У разі високої добротності схеми метод потребує дуже високої точності інтегрування системи (9). Задача визначення перехідного процесу, що описується формулою (9), дуже складна, а надійні, універсальні алгоритми для її розв’язання поки відсутні. На практиці застосовуються два можливих підходи.

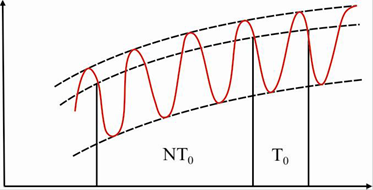
Рисунок 3 – Вихідний сигнал високодобротної електронної схеми

 

Узагальнений алгоритм Ейпріла–Тріка розглянемо на прикладі рис.4.3. Нехай задані три моменти часу t₀, t₁ і t₂, зокрема (t₂ – t₁)=T₀, (t₁– t₀)=NT₀, де N – ціле число, значення V(t₀) відомо. Якщо N вибрати так, щоб функції V_cі(t) і V_Si(t) змінювалися мало на інтервалі [t₀, t₂], то, виражаючи перші похідні цих функцій через кінцеві різниці, отримаємо

 

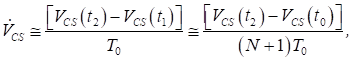                     (13)

 

де Vcs=(Vci , U, Vsi).

З огляду на (13), за допомогою формули (3) можна отримати

 

                  (14)

 

Система (14) розв’язується методом Ньютона щодо векторів V_i, i=1, 2,..., т+1, водночас для деякого значення V(t₁) необхідно чисельно проінтегрувати систему (9) на інтервалі [t₁, t₂]. Цьому методу притаманні недоліки методу Ейпріла-Тріка, пов’язані зі складністю визначення матриці [дФ/dV] і залежністю обчислювальних витрат від добротності схеми.

Метод вкладеного інтегрування багатоперіодних схем (ВІБС) оснований на спільному інтегруванні двох систем ЗДР: нелінійної (3) на періоді Т₀ (внутрішнє інтегрування); V_CS = F₁(V_CS, t), V_CS(t₀) = V₀ на інтервалі [t₀, t₁] (зовнішнє інтегрування). Оскільки вектор-функція F₁ у явному вигляді невідома, для її оцінки можна скористатися наближеною формулою

 

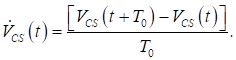                                 (15)

 

Для зовнішнього інтегрування можуть застосовуватися явні та неявні формули. В окремому випадку для інтегрування за неявною формулою Ейлера на кроці зовнішнього інтегрування H = NТ₀ отримаємо систему (11), тому ВІБС можна розглядати як узагальнення попереднього методу. Важливою відмінною рисою ВІБС є алгоритм виконання неявного кроку зовнішнього інтегрування, оснований на таких положеннях.

Внутрішнє інтегрування виконується тільки однокроковими. На кожному i-му кроці внутрішнього інтегрування h_i на інтервалі [t₁, t₂] для обраної формули інтегрування можна скласти систему рівнянь:

 

     i = 1,2,…, m.                         (16)

 

де V_i, V_i+1 та – значення фазових змінних відповідно на початку і в кінці кроку h_i, зокрема V₁ = V(t₁), V_m+1 = V(t₂).

Унаслідок цього на інтервалі [t₁, t₂] отримаємо т систем типу (4.12) з (т+1) невідомими векторами V_i. Загальна замкнута система рівнянь містить і систему, отриману для формули зовнішнього інтегрування, яка для неявної формули Ейлера має вигляд:

 

V₁ = V(t₀) + (V_i+1 – V₁)‧ H / T,                               (17)

 

H = NT₀ – крок зовнішнього інтегрування.

Ця формула еквівалентна (14). Отримані системи (9) і (10) розв’язуються методом Ньютона щодо векторів V_i, i =1, 2,..., т+1.