Розділ 3

Нерозрізні балки

 

Нерозрізною балкою називається суцільний брус, що згинається, який перекриває декілька прольотів і нерозривно пов'язаний з опорами. Такі балки досить широко застосовуються в будівництві, наприклад як підкранові балки, нерозрізні прогони покриттів, в залізобетонних ребристих покриттях і т.п.

Вони, як правило, економічніші розрізних, оскільки прольотні моменти в них менше, ніж в аналогічних розрізних.

 

 

Недоліком нерозрізних балок  є  те,  що  при  нерівномірному осіданні  опор,  навіть  при відсутності зовнішніх навантажень, в балці виникають внутрішні зусилля. Розраховують балки як методом сил, так і методом переміщень.

 

3.1. Розрахунок нерозрізних балок методом переміщень

 

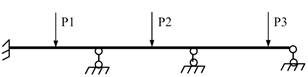
Міра лінійної рухливості нерозрізної балки завжди рівна нулю.

Міра кутової рухливості рівна числу проміжних опор, тобто для нерозрізних балок число невідомих методу переміщень визначається η=η_φ; так як. η_Δ=0. У нашому випадку η=2.

 

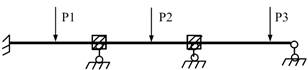
І далі як в звичайному методі переміщень

 

 

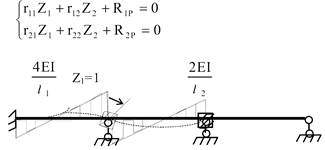
3.2. Розрахунок нерозрізних балок методом сил

 

 

Міра статичної невизначеності нерозрізної балки може бути визначена за формулою Чебишева n=С+2Ш-2D, але враховуючи, що Ш=0, а D=1, формула матиме вигляд:

 

 

Спочатку основну систему методу сил вибирали, відкидаючи «зайві» опорні зв'язки:

 

 

Одиничні епюри при такому виборі основної системи розповсюджуються на всю довжину балки і жоден з одиничних коефіцієнтів системи канонічних рівнянь не рівний нулю.

У процесі практичних розрахунків пересвідчилися, що більш раціонально основну систему вибирати, вводячи в проміжні опорні перетини перерізаючі шарніри. Як невідомі, при такому виборі основної системи, виступають опорні моменти. Одиничні епюри розповсюджуються тільки на два сусідніх прольоти і канонічні рівняння методу сил значно спрощуються, в кожному з них залишається не більш трьох невідомих.

 

 

3.2.1. Рівняння трьох моментів, як окремий випадок методу сил

 

Запишемо канонічне рівняння методу сил для опори n:

 

 

 

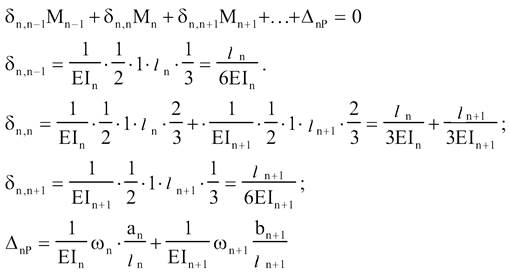
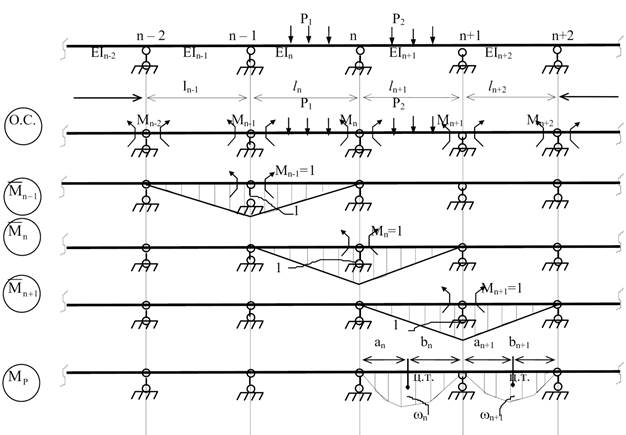
Тоді, підставляючи значення знайдених коефіцієнтів в систему канонічних рівнянь, отримаємо

 

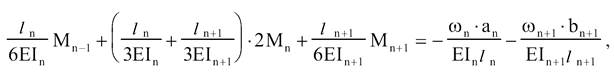
помножимо отримане рівняння на 6

 

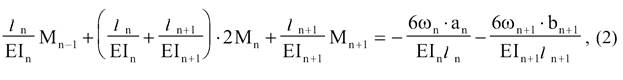
і отримуємо рівняння трьох моментів для розрахунку нерозрізних балок. Це рівняння є частковим виглядом канонічних рівнянь методу сил.

Для  балок,  що  мають  постійну  жорсткість  по  довжині  ЕІ=соnst,     що  частіше  за  все зустрічається на практиці, рівняння трьох моментів запишеться

 

 

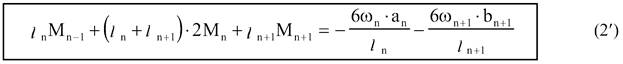
Щоб скористатися рівнянням трьох моментів, необхідно основну систему вибрати замінивши задану нерозрізну балку системою однопролітних розрізних балок, як невідомі прийняти моменти над проміжними опорами.

Опори пронумерувати, рухаючись по балці зліва направо. Пронумерувати прольоти, номер прольоту повинен відповідати номеру правої опори.

Для всіх невідомих опорних моментів записати рівняння трьох моментів, побудувати вантажну епюру, обчислити праві частини рівнянь і знайти невідомі опорні моменти.

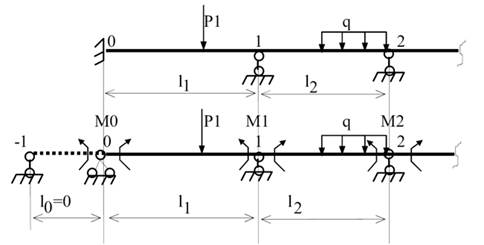
Примітка:

Якщо одна з крайніх опор - жорстке защимлення, то з боку цієї опори вводять фіктивний проліт, довжина якого рівна нулю.

 

 

 

 

 

3.3. Метод моментних фокусів

 

Якщо в нерозрізній балці завантажений тільки один проліт, то епюра згинаючих моментів в інших незавантажених прольотах являє собою прямі лінії, що перетинають вісь балки. Опорні моменти, по мірі віддалення від завантаженого прольоту меншають, епюра як би затухає.

 

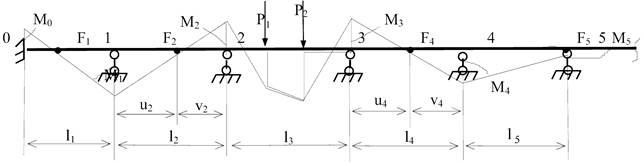
Якщо прольоти, що розглядаються, розташовані ліворуч завантаженого, то нульові точки зміщені ближче до лівих опор і називаються лівими фокусами F₁, F₂ i т.д., якщо прольоти розташовані праворуч завантаженого, то нульові точки зміщені ближче до правих опор і називаються правими фокусами F₄, F₅ і т.д.

Кожний проліт має два фокуси (лівий і правий), положення яких не залежить від діючого зовнішнього навантаження, а залежать тільки від геометрії балки.

Положення фокусних точок в прольоті визначаються їх фокусними відношеннями. Під фокусними відношеннями розуміються відношення довжин ділянок прольоту, на які ділиться цей проліт фокусною точкою. Наприклад:

 

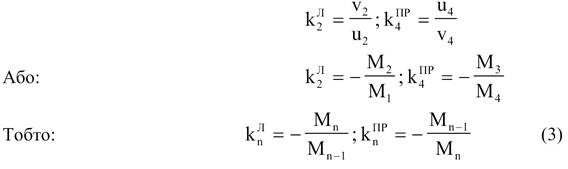
Використовуючи рівняння трьох моментів, виразимо фокусні відносини через довжини прольотів. Розглянемо незавантажену ділянку балки з опорою n-1 по середині і запишемо для неї рівняння трьох моментів:

 

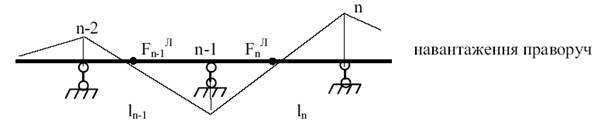
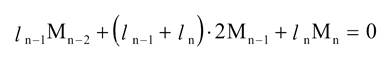
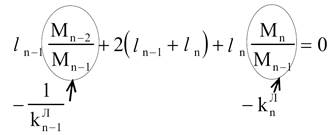
тоді

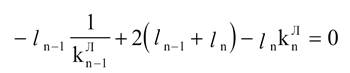
аналогічно

Тобто   фокусні  відношення  прольоту n  визначаються  через  довжини  прольотів  і   фокусні відношення сусідніх прольотів.

 

к_n^л — визначається через леві фокусні відношення попереднього лівого прольоту, а  к_n^пр  — через праве фокусне відношення попереднього правого прольоту.

Отже, фокусні відношення перших крайніх прольотів повинні бути відомі.

 

Значення фокусних відношень для крайніх прольотів

 

1. Крайня опора шарнірна

 

 є консоль, або нема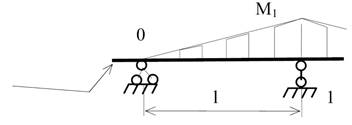

  бо                    

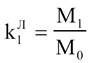
2. Права опора має жорстке защимлення

 

 

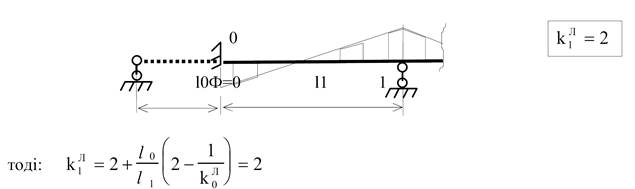
Фокусне відношення прольотів нерозрізної балки визначають використовуючи формулу (4). Ліві фокусні відносини знаходять рухаючись по балці зліва направо, а праві - зправа наліво. Фокусні відношення для перших (крайніх) прольотів відомі - вони залежать від вигляду крайніх опор.

Для побудови епюри моментів для нерозрізної балки у якої завантажений тільки один проліт, необхідно знати для всіх прольотів фокусні відношення і моменти на опорах, що примикають до завантаженого прольоту.

 

Моменти на опорах, що примикають до завантаженого прольоту

 

Розглянемо ділянку балки із завантаженим прольотом n.

 

 

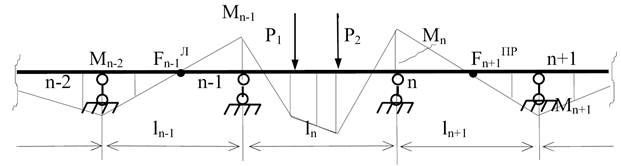
Запишемо рівняння трьох моментів для опорних моментів Мn-1 і Мn

 

 

 

 

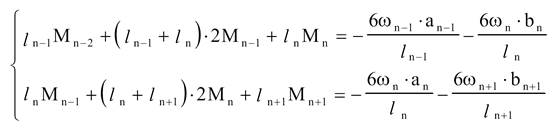
оскільки немає навантаження в прольотах

З системи рівнянь виключимо М_n-2 I M_n+1

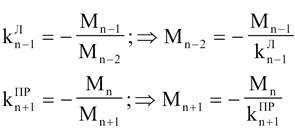
або, використовуючи формулу 4

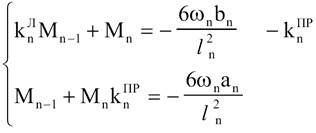
Розв’язуючи систему рівнянь:

 

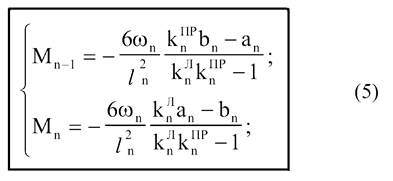
Іноді опорні моменти визначаємо через фокусні відношення:

 

 

 

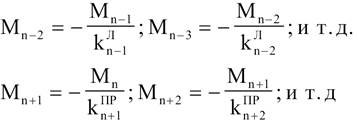
Порядок розрахунку нерозрізних балок методом моментних фокусів:

 

1)  цей метод застосуємо тільки в тих випадках, коли зовнішнім навантаженням завантажений тільки один проліт нерозрізної балки;

2)  не звертаючи уваги на зовнішнє навантаження, по формулах (4) визначають ліві і праві фокусні відносини для всіх прольотів балки;

3)  будують вантажну епюру;

4)  використовуючи формули (5), визначають моменти на опорах, що примикають до завантаженого прольоту;

5)  по формулах (3) визначають згинаючі моменти на інших опорах;

6)  будують епюру опорних моментів, і складаючи її з вантажною, отримують результуючу епюру М;

7)  при необхідності по епюрі М будують епюру Q.

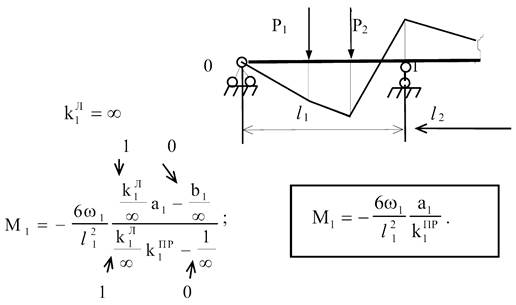
Примітка: якщо завантажений крайній проліт з шарнірною опорою

 

M₀=0; за формулою (5)

 

 

 

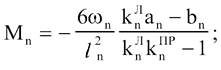
3.4. Огинаючі епюри зусиль для нерозрізних балок

 

 

Навантаження, що діють на споруду, діляться на постійні і тимчасові.

Постійні - це навантаження, величина і розміщення яких не міняється в процесі експлуатації споруди (наприклад, власна вага споруди і т.п.).

Тимчасові - це навантаження, величина і розташування яких можуть мінятися в процесі експлуатації споруди (снігові, корисні навантаження і ін.).

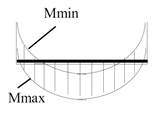
Для розрахунку нерозрізних балок за умовами міцності, тобто для підбору їх перетинів, армування і так далі, необхідно знати величини найбільших і найменших згинаючих моментів не тільки на опорах і у середини прольоту, але і в проміжних перетинах. З цією метою для нерозрізних балок будують огинаючі епюри. Крива, що з'єднує найбільші додатні значення моментів називається огинаючої М_мах, а крива, що з'єднує найбільші від’ємні значення моментів називається -М_мin.

 

Порядок побудови огинаючих епюр:

 

1.  Будується епюра М для нерозрізної балки від дії постійних навантажень (в РПР використовуючи рівняння трьох моментів).

2.  Послідовно завантажуючи кожний проліт і консолі балки тимчасовим навантаженням, будують епюри М від кожного окремого завантаження (використовуючи метод моментних фокусів).

3.  Для визначення ординат огинаючої епюри М_мах в певному перетині, необхідно до взятого зі своїм знаком значення моменту від дії постійного навантаження, алгебраїчно додати всі додатні значення моментів в даному перетині від окремих навантажень балки тимчасовим навантаженням.

4.  Ординати огинаючої  М_min отримують як алгебраїчну суму взятого зі своїм знаком значення моменту від постійного навантаження і всіх від’ємних значень моменту в цьому ж перетині від навантажень балки тільки тимчасовим навантаженням.

5.  Значення М_мах і М_min визначають в достатньому числі перетинів, розбивши проліт балки, що розглядається на 5, 10, або більше частин (в залежності від необхідної точності розрахунку).

6.  З'єднавши отримані ординати М_мах і М_min , плавними кривими, отримуємо огинаючі М_мах і М_min .

7.  У разі необхідності, аналогічно будуємо огинаючі Q_мах і Q_min

 

 

 

3.4. Лінії впливу для нерозрізних балок.

 

Для побудови лінії впливу зусиль в нерозрізних балках, використовують метод моментних фокусів.

Внутрішні зусилля в перетині балки виражають через згинаючі моменти на лівій і правій опорах, і зусилля в цьому перетині основної системи від рухомого навантаження М₀, Q₀, R₀.

 

 

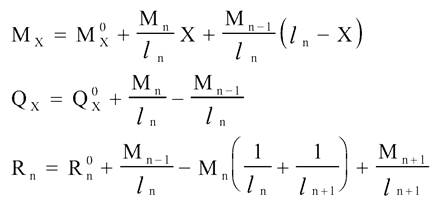
Таким чином, для побудови ліній впливу внутрішнього зусилля в нерозрізній балці необхідно заздалегідь побудувати лінії впливу опорних моментів.

Для цього, послідовно розташовуючи одиничний вантаж в кожному прольоті балки, використовуючи метод моментних фокусів, записують аналітичну залежність опорних моментів, що розглядаються від положення одиничного вантажу в прольоті. По цій залежності будують лінії впливу опорних моментів.

Наприклад:

 

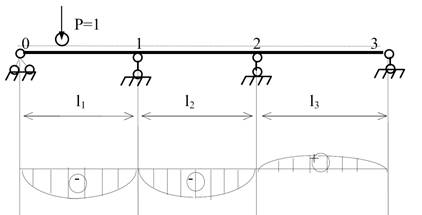л.в.М₁

 

 

 

Процес цей арифметично дуже трудомісткий і, у разі необхідності, лінії впливу будують, використовуючи довідкову літературу, або стандартні програми для ЕОМ.

Бувають випадки, коли необхідно представити вигляд лінії впливу того або іншого зусилля в нерозрізній балці. Тут зручно побудувати не саму лінію впливу, а її модель, користуючись кінематичним методом

 

 

 

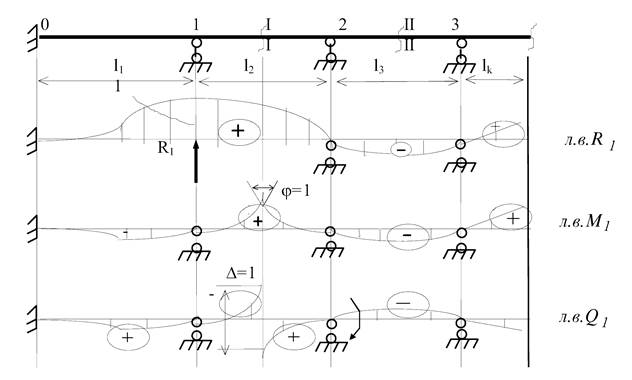
Порядок побудови:

1.  У нерозрізній балці усувається той зв'язок, який сприймає зусилля, що розглядається.

2.  У напрямі відкинутого зв'язку, балці задається одиничне узагальнене переміщення.

3.  Від цього переміщення будується деформована пружна вісь балки, яка і буде являти собою модель лінії впливу шуканого зусилля.

 

 

Питання для самоперевірки

 

1. Що називається нерозрізною балкою?

2. Які переваги та недоліки нерозрізних балок?

3. Які особливості розрахунку нерозрізних балок методом переміщень?

4. Які особливості розрахунку нерозрізних балок методом сил?

5. Що таке рівняння трьох моментів?

6. Що таке метод моментних фокусів?

7. Для чого використовуються огинаючі епюри згинальних моментів в нерозрізних балках?

8. Як побідувати модель лінії впливу для нерозрізної балки?