Розділ 2

Метод переміщень

 

Метод переміщень є таким же універсальним методом, як і метод сил, і може бути застосований для розрахунку будь-яких статично невизначних систем. Однак найбільш раціонально застосування цього методу для розрахунку статично невизначних рам і нерозрізних балок. При розрахунку інших статично невизначних систем (ферм, арок і т.д.) рішення методом переміщень виходить більш громіздким в порівнянні з методом сил, і, в ручній реалізації, для розрахунку таких систем метод переміщень, як правило, не застосовується.

У методі сил за невідомі приймалися зусилля в так званих «зайвих» зв'язках, після визначення яких ми могли знайти всі інші зусилля (М, Q, N) в будь-якому перетині, а потім, використовуючи отримані епюри визначити переміщення будь-якої точки споруди.

Але можна вирішити задачу і в іншій постановці: спочатку визначити переміщення яких-небудь точок споруди, а потім відповідні їм зусилля. Так вирішується задача в методі переміщень, де за невідомі приймаються кутові і лінійні переміщення вузлів рами.

Основні передумови методу:

1)  як і в методі сил, нехтують впливом поздовжніх і поперечних сил на переміщення вузлів рами, враховують вплив тільки згинаючих моментів;

2)   через   малість   деформацій   згину,   нехтують   зміною   довжин   стержнів   за   рахунок викривлення їх осей;

3)  у загальному випадку навантаження вузли рами можуть повертатися і лінійно зміщатися. Вважається, що при повороті жорсткого вузла всі примикаючі елементи повертаються на один і той же кут. Елементи, що сходяться в шарнірному вузлі, повертаються кожний на свій кут, в зв'язку з чим кут повороту шарнірного вузла визначити не вдається;

 

               

 

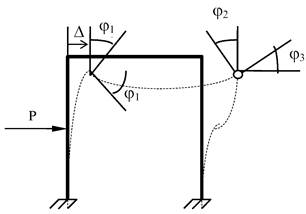
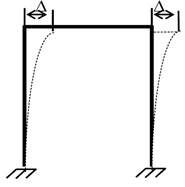
4) лінійні переміщення вузлів відбуваються по дузі кола, але в зв'язку з їх малістю вважають, що переміщення вузлів відбуваються перпендикулярно до елемента, якому вони належать.

 

 

2.1. Міра кінематичної невизначеності рам (кількість невідомих)

 

Мірою кінематичної невизначеності називається число невідомих переміщень, які визначають деформований стан системи і, отже, всі зусилля в ній. Враховуючи сказане, міра кінематичної невизначеності рами визначається:

 

 

тут η_φ - міра кутової рухливості рами. Вона визначається числом жорстких вузлів рами, не рахуючи опорних, так як їх положення заздалегідь відоме. Жорстким вважається вузол, в якому, принаймні, два з стержнів, що сходяться сполучені між собою жорстко.

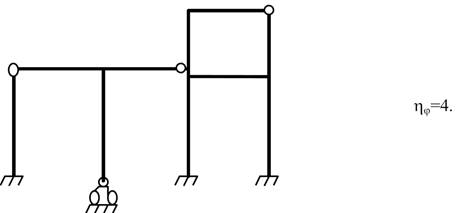
У одному вузлі може за допомогою шарніра сполучатися група жорстких вузлів, наприклад

 

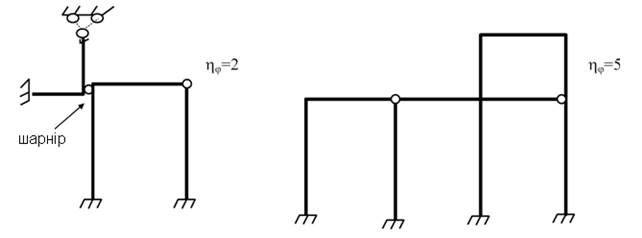
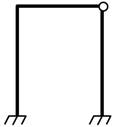
η_Δ - міра лінійної рухливості рами, рівна кількості можливих незалежних лінійних зміщень вузлів рами.

       

 

Якщо це візуально визначити важко, то задану раму перетворюють в шарнірно-стержневу систему, вводячи у всі жорсткі вузли, в тому числі і опорні, шарніри. Міра свободи отриманої системи і визначає міру лінійної рухливості рами.

Наприклад:

 

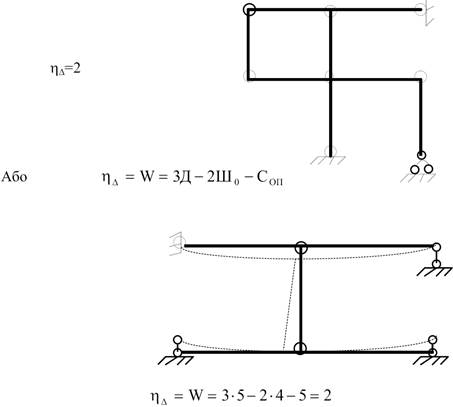
2.2. Основна система методу переміщень і канонічні рівняння

 

Після визначення числа невідомих, вибирають основну систему методу переміщень. На відміну від методу сил, де основну систему вибирають статично визначеною, в методі переміщень як основна система приймається кінематично визначена система, яка утвориться із заданої шляхом накладення на її вузли зв'язків, перешкоджаючих пружним переміщенням вузлів. Вводяться зв'язки двох типів:

а)   зв'язки першого роду,  або  пружно-податливі защемлення, які не  дають вузлам можливості повертатися, але не перешкоджають можливим їх лінійним зміщенням (моментні зв'язки)

 

 

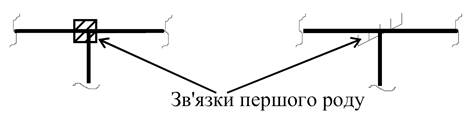
Зв'язки першого роду вводяться у всі жорсткі вузли рами.

б)  зв'язки другого роду або опорні стержні, які не заважають повороту вузлів, але виключають їх можливі лінійні зміщення

Вводять зв'язки другого роду у напрямі можливих лінійних переміщень вузлів.

Розглянемо приклад вибору основної системи методу переміщень

η=1+1=2

 

 

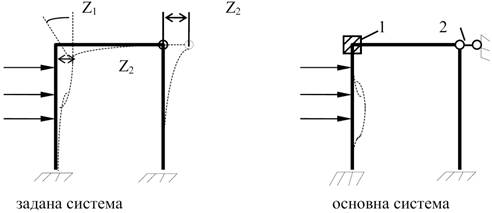
Тобто основна система являє собою набір окремих статично невизначних балок з постійною жорсткістю.

Ідея методу: для того, щоб основна і задана система були рівноцінні в значенні деформацій і зусиль, необхідно в основній системі зв'язки повернути на відповідні кути і додати їм лінійні зміщення як в заданій системі. При цьому в додаткових зв'язках виникнуть реактивні зусилля. У зв'язках першого роду реактивні моменти, а в зв'язках другого роду реакції. Оскільки в заданій системі додаткових зв'язків немає, то можна записати умови рівноцінності: реактивні зусилля в додаткових зв'язках від їх переміщення і дії зовнішнього навантаження повинні бути рівні нулю, тобто

 

 

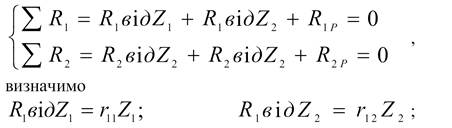
де:

r₁₁   — реактивне зусилля в зв’язку   1   від одиничного зміщення зв’язка Z₁=1, тобто індекси при коефіцієнтах позначають

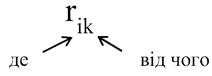
Тоді,  система канонічних рівнянь  методу переміщень  для  систем з  двома невідомими запишеться

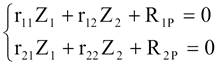
Для n - разів кінематично невизначних систем

 

 

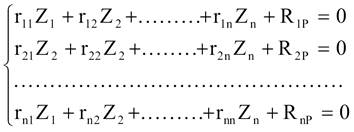
2.3. Визначення коефіцієнтів і вільних членів канонічних рівнянь

 

Як вказувалося вище, завдяки введенню додаткових зв'язків, основна система методу переміщень являє собою набір окремих статично невизначних балок постійної жорсткості по довжині. Їх опорні закріплення можуть бути двох типів: жорстке защемлення або шарнір (див. мал. а і б)

 

Оскільки ми нехтуємо поздовжніми деформаціями елементів, то можливими переміщеннями вузлів балок а) і б) є вертикальні лінійні переміщення і поворот жорстко закріпленого вузла.

Коефіцієнти, що входять в канонічні рівняння, являють собою реактивні зусилля в додаткових зв'язках від переміщень вузлів і дії зовнішніх навантажень. Тому розглянемо напружено-деформований стан окремих балок від різних можливих видів впливів.

 

Аналогічно вирішуючи задачу для інших можливих видів впливів, формують таблицю напружено-деформованих станів окремих балок.

 

 

 

 

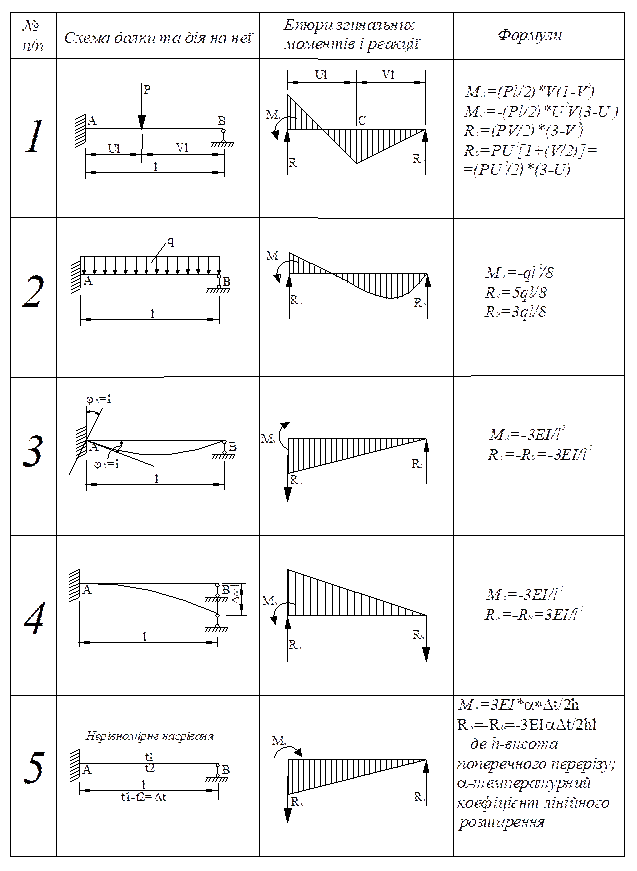
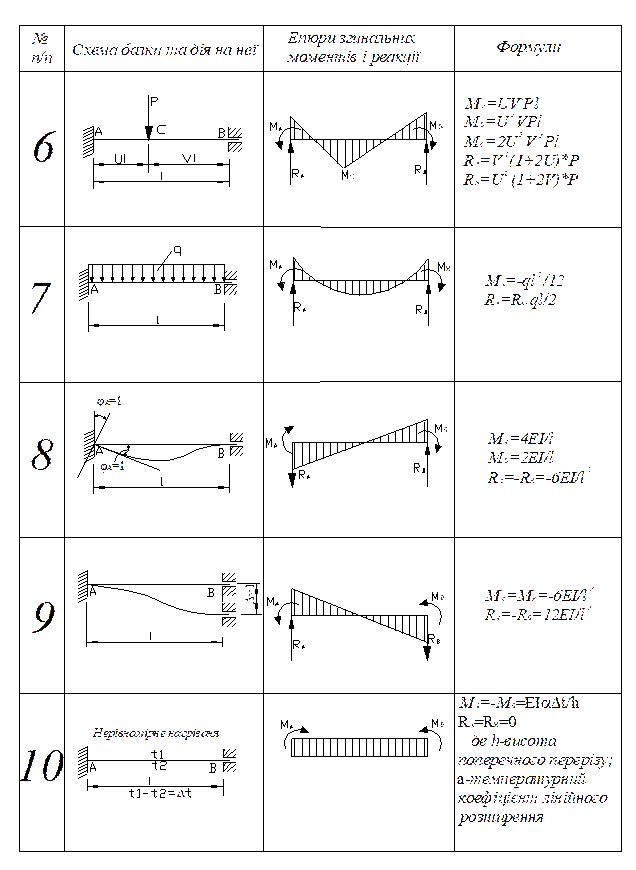
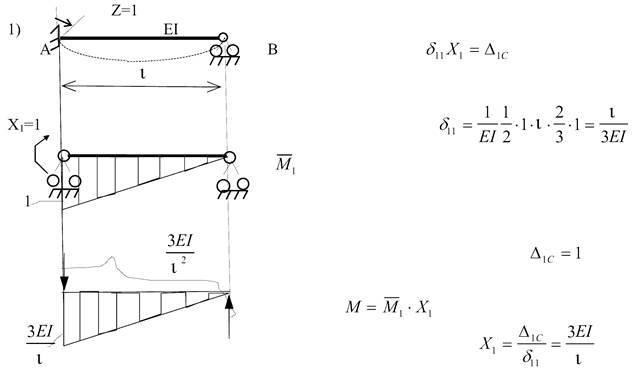
Порядок визначення коефіцієнтів розглянемо на конкретному прикладі:

 

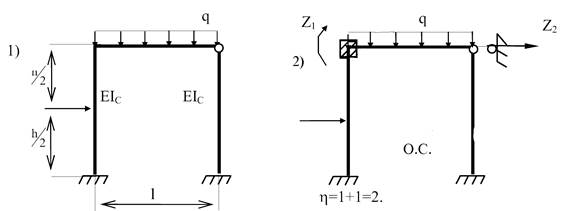
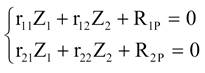
1е   рівняння називається моментним;

2е   рівняння - рівнянням зсуву.

4) Для визначення коефіцієнтів канонічних рівнянь необхідно побудувати одиничні і вантажну епюри. Епюри будують в основній системі методу переміщень, послідовно задаючи одиничні зміщення всім додатковим накладеним зв'язкам і від дії зовнішнього навантаження, використовуючи раніше складену таблицю.

 

 

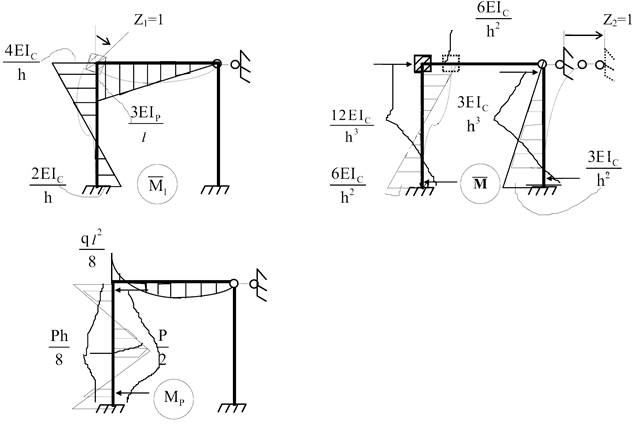
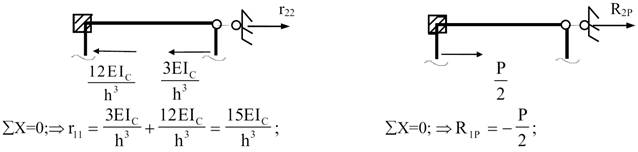
Коефіцієнти моментних рівнянь, що являють собою реактивні моменти в додаткових зв'язках визначають шляхом вирізування цих додаткових зв'язків з відповідних епюр. До зв'язку, що вирізається прикладають реактивні моменти, взяті з епюр і шукану реакцію зв'язку. Шукану реакцію прикладають так, як задавалося одиничне переміщення зв'язку. Сума усіх моментів зв’язку має бути нульова. З цієї умови визначають шукану реакцію.

r_іі -   реактивний момент в першому зв'язку від її одиничного зміщення.

 

Коефіцієнти рівнянь зсуву, що являють собою реактивні зусилля в зв'язках другого роду, визначають, відрізаючи від рами елемент, через який передаються реакції на зв'язок, що розглядається, вздовж якого розташований додатковий опорний стержень. До відсіченого опорного елементу прикладають шукану опорну реакцію (у напрямі, якій задавали одиничному переміщенню) і реакції стержнів, які проектуються на вісь додаткового стержня.

З рівняння, у вигляді суми проекцій всіх сил на напрям одиничного переміщення, визначаємо величину шуканої реакції.

 

5) Перевірки коефіцієнтів системи канонічних рівнянь (виконують досить рідко):

а) універсальна: сума всіх одиничних коефіцієнтів рівна результату множення сумарної одиничної епюри самої на себе:

 

6) пострічкова перевірка: сума всіх одиничних коефіцієнтів і-го рівняння дорівнює результату множення сумарної одиничної епюри на М_і

в) перевірка вантажних коефіцієнтів: сума всіх вантажних коефіцієнтів рівна, взятому із зворотним знаком, результату множення сумарної одиничної епюри на вантажну, побудовану для основної системи методу сил:

6) Коефіцієнти підставляють в систему канонічних рівнянь і розв’язують її, визначаючи невідомі Z₁, Z₂, … Z_n

7)  Після того, як знайдені дійсні переміщення додаткових зв'язків Z_i, будують кінцеву епюру зусиль в заданій системі.

Епюру згинаючих моментів М_рез   отримують складанням ординат вантажної епюри Мр з ординатами виправлених епюр М_ІZ_І, тобто:

Правильність побудови кінцевої епюри згинаючих моментів перевіряють тими ж способами, що і в методі сил:

а)   перевіряється рівновага вузлів рами - в методі переміщень ця перевірка є істотною, оскільки в основній системі рівності моментів у вузлі немає, а в заданій системі вона повинна виконуватися;

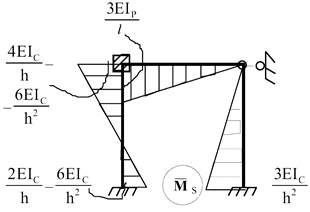
б)  виконується деформаційна перевірка. Для цього вибирається основна система методу сил, будується одна з можливих одиничних епюр і:

По епюрі моментів будують епюру Q, а по епюрі Q - епюру поздовжніх сил N.

 

 

 

2.4. Використання симетрії при розрахунку рам методом переміщень

 

При розрахунку симетричних систем методом переміщень, так само як і при розрахунку методом сил, можна застосовувати групування невідомих.

У цьому випадку усі епюри від одиничних невідомих будуть симетричними, або оберненосиметричними. Ряд побічних коефіцієнтів перетворюється на нуль. Розрахунок значно спрощується:

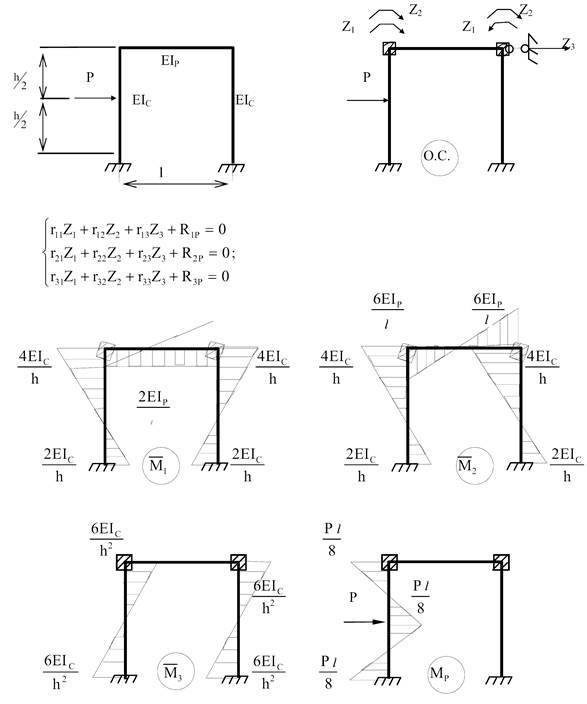
При визначенні коефіцієнтів системи канонічних рівнянь необхідно пам'ятати, що реакції, як і переміщення, є груповими і являють собою алгебраїчну суму реакцій в зв'язках даної групи.

Наприклад, для визначення реакції r₁₁ необхідно на першій епюрі вирізати два зв'язки і тоді

 

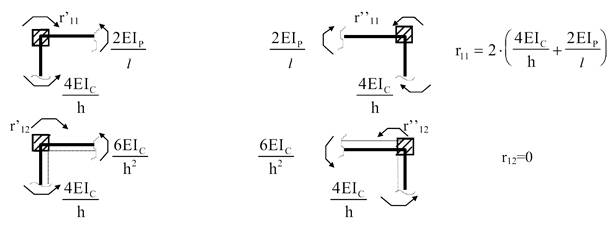
тобто симетрична групова реакція від кососиметричного групового переміщення дорівнює нулю

Система з трьох рівнянь розпадається на одне рівняння і систему з двох рівнянь з двома невідомими.

При окремих видах навантаження розрахунок ще більш спрощується. Так, при дії на симетричну раму симетричного навантаження в задачі залишаться тільки симетричні невідомі переміщення, кососиметричні будуть рівні нулю. При дії кососиметричного навантаження залишаються невідомими тільки кососиметричного переміщення.

Наприклад, на раму діє симетричне рівномірно-розподілене навантаження

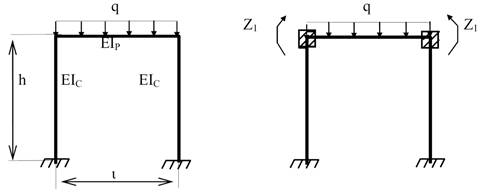
У загальному випадку число невідомих методу переміщень η=3, але враховуючи що Z₂=Zз=0, залишається одне невідоме

 

 

Питання для самоперевірки

 

1. Які системи краще розв’язувати за допомогою методу переміщень?

2. Як визначити ступінь кінематичної невизначеності рами?

3. Як вибрати основну систему в методі переміщень?

4. Що таке зв’язки першого роду та другого роду в основній системі?

5. Поясніть суть величин, що входять в канонічні рівняння методу переміщень, а також суть самого рівняння.

6. Як побудувати одиничні епюри в методі переміщень?

7. Як побудувати вантажні епюри в методі переміщень?

8. Поясніть як визначити одиничні та вантажні коефіцієнти в канонічних рівняннях методу переміщень?

9. Як перевірити правильність знаходження одиничних та вантажних коефіцієнтів?

10.          Що потрібно для побудови кінцевої епюри моментів?

11.          Як використовується симетрія рам при розрахунку методом переміщень?