Розділ 7

Змішаний метод розрахунку рам

 

Розглянуті раніше метод сил і метод переміщень можуть бути використані при розрахунку самих довільних статично невизначних систем. Однак кожний з них має свою раціональну область застосування. Наприклад, для рам з прямолінійними стержнями, що мають в основному жорсткі вузли, раціональніше застосовувати метод переміщень. У шарнірно-стержневих системах, в системах зі стержнями ламаного контура, невідомих методу сил звичайно менше, ніж методу переміщень.

 

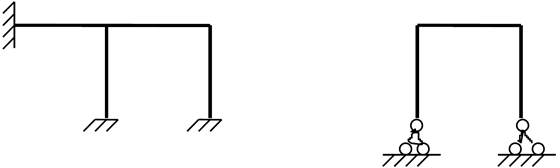
М.п.  n=2                                                                М.п. n=3

М.c.  n=6                                                                М.c. n=1

 

Зустрічаються системи, в яких можна виділити одну частину більш зручну для розрахунку методом переміщень, а інша більш зручна для розрахунку методом сил.

 

 

 

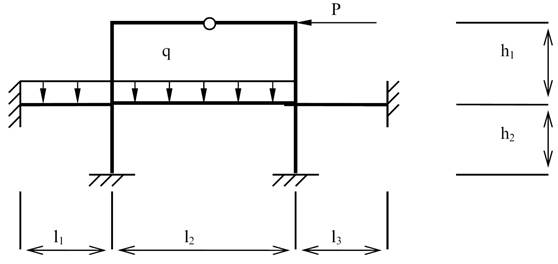
Як видно з таблиці, в даному випадку перший поверх більш раціонально розв’язувати методом переміщень, а другий - методом сил.

Метод, в якому приймають частину невідомих методу сил, а частину - методу переміщень, називається змішаним. Запропонований метод Ф. Блейхом (кінець XIX ст.) і розвинений в канонічній формі А.А. Гвоздєвим (1927 рік).

 

 

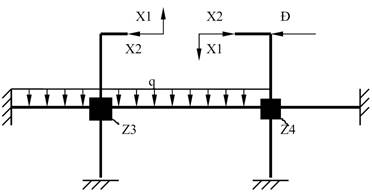
Умовами еквівалентності заданої і основної систем в цьому випадку будуть рівність нулю переміщень у напрямі невідомих Х₁ і Х₂ і рівності нулю реактивних зусиль в зв'язках 3 і 4. У канонічній формі ці умови запишуться:

 

 

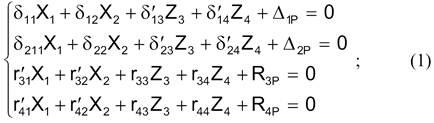
Рівняння (1) - канонічні рівняння змішаного методу.

Коефіцієнти δ_ik, визначають як в методі сил, шляхом перемноження епюр за допомогою інтеграла Мора:

 

 

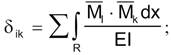
для обчислення, якого можна використати правило Верещагіна або формулу Сімпсона, δ_ik=δ_kі

Коефіцієнти r_ік - визначають як в звичайному методі переміщень. Це реактивне зусилля в зв’язку і від одиничного зміщення зв’язка k. r_ік=r_ік

Між коефіцієнтами з штрихами існує зв'язок:

 

r^/_ік=-δ^/_kі,

 

і простіше визначити r^/_ік який представляє собою реактивне зусилля в зв'язку і від дії сили Хк = 1 , а потім прирівнюють δ^/_kі=-r^/_ік

Або δ^/_kі визначають з епюри переміщень. Змішаний метод має переваги над іншими в тих випадках, коли одна частина рами має підвищену рухливість, а інша -    підвищену жорсткість.

Приклад

 

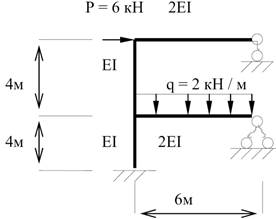
Питання для самоперевірки

 

1. Який метод розрахунку називається змішаним?

2. Які системи краще розв’язувати за допомогою змішаного методу?

3. Які умови еквівалентності заданої та основної системи у змішаному методі розрахунку?

4. Які особливості канонічних рівнянь в змішаному методі?

5. Який існує зв’язок між одиничними коефіцієнтами системи канонічних рівнянь?