ТЕМА №5

Обробка результатів спостережень

при багаторазових вимірюваннях

План

1.   Характеристика багаторазових вимірювань.

2.   Порядок оброблення результатів спостережень при багаторазових вимірюваннях.

3. Визначення точкових оцінок закону розподілу результатів спостережень.

 

1. Характеристика багаторазових вимірювань.

Багаторазові вимірювання - це вимірювання однієї або декількох величин, виконане чотири і більше разів. Багаторазове вимірювання являє собою ряд одноразових вимірювань. Мінімальна кількість вимірювань, при якому вимірювання може вважатися багаторазовим - чотири. Результатом багаторазового вимірювання є середнє арифметичне результатів всіх проведених вимірювань. При багаторазових вимірюваннях знижується похибка. Багаторазові вимірювання проводятьтся при наукових дослідженнях, повірці засобів вимірювальної техніки.

2. Порядок оброблення результатів спостережень при багаторазових вимірюваннях складається з ряду послідовно виконуваних етапів:

1) визначення точкових оцінок параметрів законів розподілу результатів вимірювань. На цьому етан після ранжирування значень вибірки (Х) в порядку зростання і представлення її у вигляді варіаційного ряду  визначаються:

а) оцінка центру розподілу ;

б) оцінка середньоквадратичного відхилення СКВ окремих результатів спостережень ;

в) оцінка СКВ середнього арифметичного значення .

 Відповідно до критеріїв виключаються грубих похибок (промахи)  вводяться поправки на систематичні похибки. Після їх виключення проводиться повторний розрахунок оцінок середнього арифметичного значення і оцінок СКВ спостережень і вимірювань;

2) визначення оцінок параметрів закону розподілу результатів вимірювань або випадкових похибок вимірювань. У цьому випадку від вибірки результатів вимірювань х1, х2, ... , хn переходять до вибірки відхилень від середнього арифметичного Δх1, Δх2, ... , Δхn.

Для оцінки параметрів закону розподілу проводиться побудова за виправленими результатами вимірювань хі, де і = 1,2, ..., n - члени варіаційного ряду (впорядкованої вибірки) yi, де yi=min(хi) і yi=max(хi). По виду статистичних функцій розподілів (представлених у вигляді гістограм або полігонів - для диференціальної форми або у вигляді кумулятивної кривої - для інтегральної форми) може бути оцінений закон розподілу результатів спостережень.

3) оцінка закону розподілу по статистичним критеріям. Для перевірки гіпотез про вигляд функції розподілу експериментальних даних використовують наступні критерії: Пірсона, Мізеса-Смірнова, складений критерій d. При числі спостережень n> 50 для ідентифікації закону розподілу використовується критерій Пірсона або критерій Мізеса-Смирнова. При 15<n<50 для перевірки нормальності закону розподілу застосовується складений критерій. При n< 15 приналежність експериментального розподілу до нормального не перевіряється. При цьому визначення довірчих меж випадкової похибки результату вимірювання за методикою, можлива в тому випадку, якщо заздалегідь відомо, що результати спостережень належать нормальному розподілу. У разі якщо гіпотеза про приналежність отриманих результатів до нормального закону розподілу не підтверджується, то проводиться наближена оцінка параметрів законів розподілу (ідентифікацією форми та виду закону розподілу відповідному теоретичному);

4) визначення довірчих інтервалів випадкової похибки. Якщо вдалося ідентифікувати закон розподілу результатів вимірювань, то з його використанням знаходять квантильний множник zp при заданому значенні довірчої ймовірності Р. У цьому випадку довірчі межі випадкової похибки знаходяться за формулою: .

5) визначення меж невиключеної систематичної похибки результату вимірювань. Під цими межами розуміють знайдені нестатистичними методами межі інтервалу, всередині якого знаходиться невиключена систематична похибка. Вона утворюється з ряду складових, як правило, похибок методу і засобів вимірювань, а також суб'єктивної похибки.

6) визначення довірчої межі похибки результату вимірювання Δр. Дана операція здійснюється шляхом підсумовування СКВ випадкової складової  і меж невиключеної систематичної складової в залежно від співвідношення цих похибок між собою.

7) формування результату вимірювань.

3.  Визначення точкових оцінок закону розподілу результатів спостережень.

Числові характеристики випадкової величини, отриманих за результатами вибіркових спостережень, тобто оцінки істинних значень поділяються на три види:

1.     Характеристики положення;

2.     Характеристики розсіяння;

3.     Характеристики форми розподілу.

До характеристик положення відносять:

-         середнє арифметичне значення ;

-         медіана ;

-         мода .

Усі ці числові характеристики визначають координату центру розподілу впорядкованої сукупності. Варто відмітити, що лише при нормальному закону розподілу усі вони співпадають між собою і можуть бути прийняті за центр розподілу статистичної сукупності фізичної величини, отриманої при вимірюваннях.

До характеристик розсіювання значень змінної величини відносять:

-         мінімальне та максимальне значення;

-         розмах варіаційного ряду ;

-         дисперсія ;

-         середньоквадратичне відхилення ;

-         середньо-квадратичне відхилення середнього значення .

Визначення вибіркового середнього арифметичного

Його визначаєм за формулою:

                                                     (1)

де хі – окремі результати вимірювань;

     n – загальна кількість результатів.

Вибіркове середнє арифметичне  являється незміщенною оцінкою любого закону розподілу. Окрім того, ефективною і достатньою характеристикою повноти всієї використовуваної у вибірці інформації. Однак оцінка у вигляді середнього арифметичного слабо захищена від впливу промахів. Середнє арифметичне 90% вибірки  менш чутливе до результатів з грубими похибками, ніж вибіркове середнє-арифметичне , оскільки при 90% вибірці відкидаються з кінців варіаційного ряду по 5 відсотків найбільш віддалених результатів, в яких можуть міститися грубі похибки.

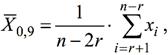                                                (2)

де 2r – число не врахованих результатів.

Медіана спостережень.

Медіаною  значення хі , яке ділить варіаційний ряд на дві частини, рівних по числу варіант. Вона визначається за формулою:

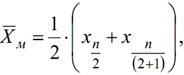                                          (3)

де n - парне число результатів вимірювань.

Якщо n непарне, використовують наступну залежність:

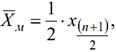                                                 (3)

Медіана  являється ефективною оцінкою центру експоненціальних розподілів.

Центр розмаху .

Для обмежених розподілів (наприклад рівномірний) ефективною оцінкою центру розподілу може бути центр розподілу варіаційного ряду, який визначається за формулою:

                                            (4)

де х1 хn – крайні значення варіаційного ряду. Однак ця оцінка дуже чутлива до результатів з грубими похибками, так як вона визначається по найбільш віддаленим від центру розподілу результатам спостережень, якими і є промахи.

Визначення середньоквадратичного відхилення .

Визначення середньоквадратичного відхилення  закону розподілу може бути проведено за формулою:

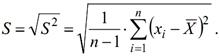                                         (5)

Середньоквадратичного відхилення середнього значення .

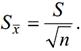                                                         (6)

Розглянемо на прикладі послідовність визначення оцінок центра розподілу. Дано результати  20 вимірювань переміщення для точок пера лопатки компресора під дією центробіжної сили. Результати спостережень і частота їх появи наведені в табл. 1.

Таблиця 1.

Визначаєм оцінку центра як:

-         середнє арифметичне за формулою:

-         середнє арифметичне 90% вибірки визначаєм за формулою:

   

 5 процентів  вибірки в нашому випадку 0,05*20=1. Тобто один результат вимірювань. Відбираєм по 1 результату вимірюювань з кінців варіаційного ряду тобто х1=23,0 мкм та х20=23,7 мкм. Тоді:

-         оскільки n парне медіану розподілу визначаєм за формулою:

 

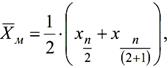
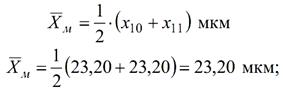
-         центр розмаху визначаєм визначаєм за формулою:

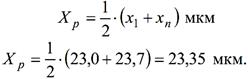
-         оцінку середньоквадратичного відхилення визначаєм за формулою:

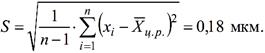
-         оцінку середньоквадратичного середнього значення визначаєм за формулою:

                                          

 

  Контрольні запитання

1.  Що являє собою багаторазове вимірювання?

2. У яких випадках проводяться багаторазові вимірювання?

3. Чому рівне значення шуканої величини при багаторазовому вимірювані?

4. Яка послідовність оброблення результатів багаторазового вимірювання?

5. Чому рівна абсолютна похибка при багаторазовому вимірювані?

6. Які точкові оцінци закону розподілу результатів спостережень Вам відомі?