ТЕМА №4

Груба похибка та методи її виключення

План

1.   Характеристика грубої похибки.

2.  Методи виключення грубої похибки.

 

1.   Характеристика грубої похибки. Грубі похибки (промахи) відносяться до числа похибок, що змінюються випадковим чином при повторних вимірюваннях. Вони явно перевищують за своїм значенням похибки, виправдані умовами проведення експерименту.

Під промахом розуміється значення похибки, відхилення якого від центру розподілу істотно перевищує значення, виправдане об'єктивними умовами вимірювання. Тому з точки зору теорії ймовірності поява промаху малоймовірна. Причинами грубих похибок можуть бути неконтрольовані зміни умов вимірювань, несправність, помилки оператора та ін. Для виключення грубих похибок застосовують апарат перевірки статистичних гіпотез. У метрології використовуються статистичні гіпотези, під якими розуміють гіпотези про вид невідомого розподілу, або про параметри відомих розподілів.

Приклади статистичних гіпотез:

1) розглянута вибірка (або її окремий результат) належить генеральної сукупності;

2 ) генеральна сукупність розподілена за нормальним законом;

3 ) дисперсії двох нормальних сукупностей рівні між собою.

 У двох перших гіпотезах зроблено припущення про вид невідомого розподілу та приналежності окремих (підозрілих) результатів даному виду розподілу, а в третій – про параметри двох відомих розподілів. Поряд з висунутою гіпотезою розглядають і суперечливу їй гіпотезу. Нульовою (основною) називають висунуту гіпотезу. А конкуруючу (альтернативну) називають ту , яка суперечить нульовий. При висуванні та прийнятті гіпотези можуть мати місце такі чотири випадки:

1) гіпотеза приймається, причому і в дійсності вона правильна;

2) гіпотеза вірна, але помилково відкидається. Виникає при цьому помилку називають помилкою першого роду, а ймовірність її появи називають рівнем значущості і позначають q (α);

3) гіпотеза відкидається, причому в дійсності вона неправильна;

4) гіпотеза неправильна, але помилково приймається. Виникаючу при цьому помилку називають помилкою другого роду, а ймовірність її появи позначають β. Величину 1- β, тобто ймовірність, що гіпотеза буде відкинута, коли вона помилкова, називають потужністю критерію.

Слід зауважити, що в нормативній документації по статистичному контролю якості продукції і підручниках з управління якістю ймовірність визнати непридатною партію придатних виробі (тобто, зробити помилку першого роду) називають "ризиком виробника", а ймовірність прийняти непридатну партію – "ризиком споживача".

Нульова статистична гіпотеза підтверджує приналежність перевірюваного "підозрілого" результату вимірювання (спостереження) до цієї групи вимірювань. Формальним критерієм аномальності результату спостережень (а, отже, і підставою для прийняття конкуруючої гіпотези: "підозрілий" результат не належить даній групі вимірювань) при цьому використовується межа, віднесена від центру розподілу на величину tS , тобто :

,                                                       (1)

де  – результат спостереження , що перевірявся на наявність грубої похибки;

       t – коефіцієнт, що залежить від виду та закону розподілу, об’єму вибірки, рівня значимості.

Таким чином, межі похибки залежать від виду розподілу, об’єму вибірки та обраної довірчої ймовірності.

При обробці вже наявних результатів спостережень довільно відкидати окремі результати не слід, так як це може призвести до фіктивного підвищення точності результату вимірювань. Група вимірів (вибірка) може містити кілька грубих похибок і їх виключення проводять послідовно, по одному.

2. Методи виключення грубої похибки. Всі методи виключення грубих похибок (промахів) можуть бути розділені на два основних типи:

а) методи виключення при відомому генеральному СКВ;

б) методи виключення при невідомому генеральному СКВ.

Оскільки на практиці частіше зустрічаються вимірювання при невідомому СКВ (обмежене число спостережень), у роботі розглянуті наступні критерії перевірки підозрілих (з точки зору похибок) результатів спостережень: Ірвіна, Романовського, варіаційного розмаху, Діксона, Смірнова та Шовене.

Критерій Ірвіна. Для отриманих експериментальних даних визначають коефіцієнт за формулою:

 ,                                                        (2)

де – найбільші значення випадкової величини;

S – середньоквадратичне відхилення, обчислене за всіма значеннями вибірки.

Потім цей коефіцієнт порівнюється з табличним значенням , можливі значення якого наведені в таблиці 1.

Якщо >, то нульова гіпотеза не підтверджується, тобто результат –помилковий, і він повинен бути виключений при подальшій обробці результатів спостережень.

Таблиця 1

Критерій Ірвіна

 

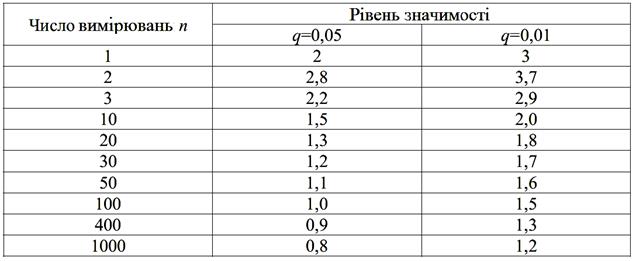
Критерій Романовського. Конкуруюча гіпотеза про наявність грубих похибок у підозрілих результатах підтверджується, якщо виконується нерівність:

,                                                     (3)

де t – квантиль розподілу Стьюдента при заданій довірчої ймовірності з числом ступенів вільності k=n-kn (kn – число підозріливих результатів спостережень).

Квантилі для розподілу Стьюдента представлені у таблиці 2. Точкові оцінки розподілу  і СКВ (S)  результатів спостережень обчислюється без урахування kn підозріливих результатів.

 

 

 

 

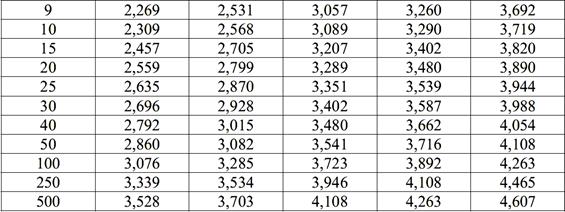
Таблиця 2

 

Критерій Стьюдента tp (Квантилі Стьюдента)

 

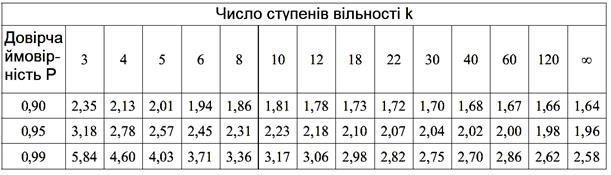
Критерій варіаційного розмаху. Цей критерій є одним з простих методів виключення грубої похибки вимірювань (промаху). Для його використання визначають розмах варіаційного ряду впорядкованої сукупності спостережень :

.                                                       (4)

Якщо який-небудь член варіаційного ряду, наприклад хk, різко відрізняється від усіх інших, то роблять перевірку, використовуючи наступну нерівність:

,                                        (5)

де – вибіркове середнє арифметичне значення, обчислене після виключення передбачуваного промаху;

z – критеріальне значення.

Нульову гіпотезу (про відсутність грубої похибки) приймають, якщо зазначенf нерівність виконується. Якщо  не задовольняє умову 5, то цей результат виключають з варіаційного ряду. Коефіцієнт z залежить від числа членів варіаційного ряду n, що представлено в таблиці 3.

Таблиця 3

Критерій варіаційного розмаху

 

Критерій "3ό" , Райта.  Критерій " правило трьох сігм " є одним з найпростіших для перевірки результатів, що підкоряються нормальному закону розподілу. Сутність правила трьох сігм: якщо випадкова величина розподілена нормально, то абсолютна величина її відхилення від математичного сподівання не перевищує потроєного середнього квадратичного відхилення.

На практиці правило трьох сігм застосовують так: якщо розподіл досліджуваної випадкової величини невідомий, однак умова, зазначена в наведеному правилі, виконується, то є підстави припускати, що досліджувана величина розподілена нормально; в іншому випадку вона не розподілена нормально.

З цією метою для вибірки (включаючи підозрілий результат) обчислюється центр розподілу і оцінка СКВ результату спостережень. Результат, який задовольняє умову:

,                                                   (6)

вважається таким, який має грубу похибку і видаляється, а раніше обчислені характеристики розподілу уточняються.

Цьому критерію аналогічний критерій Райта, заснований на тому, що якщо залишкова похибка більша чотирьох сігм, то цей результат вимірювання є грубою похибкою і повинен бути виключений при подальшій обробці. Обидва критерії надійні при числі вимірювань більше 20...50. Їх доцільно застосовувати, коли відома величина генерального середньоквадратичного відхилення.

Критерій Смірнова. Критерій Смірнова використовується при відомих значеннях генеральних середнього  та СКВ (S). Він встановлює менш жорсткі межі грубої похибки. Для реалізації цього критерію обчислюються дійсні значення квантилів розподілу (спостережуване значення критерію ) за формулою:

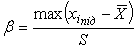.                                                     (7)

Знайдене значення порівнюється з критеріальним , що наведене в таблиці 4.

Таблиця 4

Квантилі розподілу

 

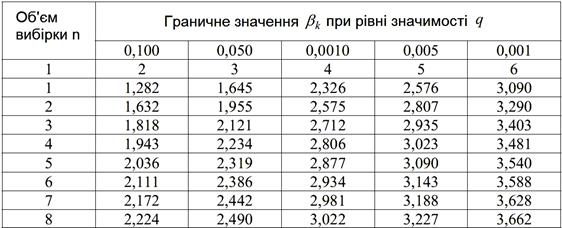
Критерій Шовене. Критерій Шовене застосовується для законів, що не суперечать нормальному, і будується на визначенні числа очікуваних результатів спостережень nоч, які мають настільки ж великі похибки, як і підозрілий результат. Гіпотеза про наявність грубої похибки приймається, якщо виконується умова:

.                                                      (8)

Порядок перевірки гіпотези наступний:

1) обчислюються середнє арифметичне  і СКВ S результатів спостережень для всієї вибірки;

2) з таблиці нормованого нормального розподілу (Додаток В – інтегральна функція нормованого нормального розподілу) за величиною:

  визначається ймовірністьпояви підозрілого результату у генеральній сукупності чисел n:

.                                           (9)

3) число очікуваних результатів  визначається за формулою:

.                                               (10)

Зазначені вище критерії в багатьох випадках виявляються "жорсткими". Тоді рекомендується користуватися критерієм грубої похибки k залежних від об’му вибірки n і прийнятої довірчої ймовірності Р.

 

 

 

 

 

 

Таблиця 5

Залежність критерія грубої похибки k від об’му вибірки n і прийнятої довірчої ймовірності Р

 

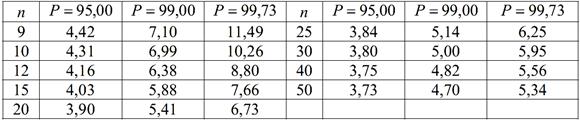
Для рівномірного розподілу за межу грубої похибки можна прийняти величину:

 Δгр=±1,8•S.                                                  (11)

де S – середньоквадратичне відхилення результатів вимірювань.

Контрольні запитання

1.  Що являє собою груба похибка?

2. Що являє собою критерій варіацяйного розмаху?

3. Що являє собою правило 3 сігм?

4. Що являє собою критерій Романовського та Діксона?

5. Що являє собою критерій Шовене та Смірнова?