Практичне заняття №6

Тема: Оброблення результатів непрямих вимірювань

Мета: Освоїти методику оброблення результатів непрямих вимірювань

 

Теоретичні відомості

Якщо випадкова величина Y повязана з незалежними випадковими величинами Y1, Y2 … Yn відомою функціональною залежністю Y=F(Y1, Y2… Yn), то знаючи математичне сподівання my1, my2 … myn та середньоквадратичне відхилення Sy1, Sy2 … Syn величин Y1, Y2 … Yn можна наближено знайти математичне сподівання my, середньоквадратичне відхилення Sy та величину Y за формулою  Y=F(Y1, Y2… Yn).

Нехай Y1, Y2 … Yn – випадкові результати незалежних прямих вимірювань різних фізичних величин а Y=F(Y1, Y2… Yn) – результат непрямого вимірювання.

Тоді математичне сподівання середньоквадратичне відхилення Sy випадкової похибки результату непрямого вимірювання можна знайти за формулою 1 та 2.

my =F(my1, my2 … myn).                                           (1)

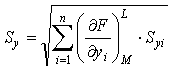,                                                (2)

де: – похідна функції F(Y1, Y2… Yn) по yi взята в точці (my1, my2 …myn).

Нехай Y1, Y2 … Yn – випадкові результати незалежних прямих вимірювань різних фізичних величин а Y=F(Y1, Y2… Yn) – результат непрямого вимірювання.

Тоді середньоквадратичне відхилення Sy випадкової похибки результату непрямого вимірювання можна знайти за формулою 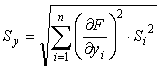3.

,                                               (3)

де Si – середньоквадратичне відхилення випадкової похибки результату прямого вимірювання Yi, а частинна похідна береться в точці y1, y2, yn які відповідають прямим вимірюванням.

Завдання

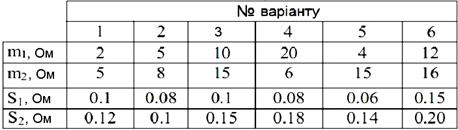
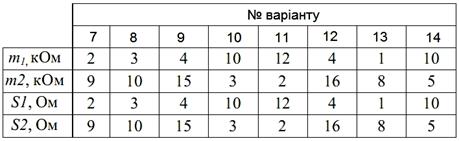
Відомі математичні сподівання і середньоквадратичне відхилення опорів R1, R2; m1=12 Ом; m2=15 Ом; S1=0,10 Ом; S2 = 0,14 Ом. Знайти математичне сподівання і середньоквадратичне відхилення послідовного і  паралельного з'єднання  опорів R1  і  R2, відносну та абсолютну похибку вимірювання опору R.  Дані   для  різних  варіантів  наведені  в таблиці 1.

 

Таблиця 1

                Вихідні дані

Приклад розв’язання для паралельного з’єднання опорів

Опір R складається з паралельно з’єднаних опорів R1 та R2, математичне сподівання та середньоквадратичне відхилення яких відомі:

m1=12 Ом; m2=15 Ом; S1=0,10 Ом; S2=0,14 Ом.

Знайти математичне сподівання m(R) та середньоквадратичну похибку S12 опору R.

При паралельному з’єднані еквівалентний опір R складе: .

Отже математичне сподівання складе:  Ом.

Для знаходження SR знаходимо спочатку частинні похідні:

           

 

Абсолютна похибка вимірювання опору R рівна:

 Ом

Відносна похибка складе:

Контрольні запитання

1.               Що являє собою непряме вимірювання?

2.               У чому полягає та яка послідовність оброблення результатів непрямих вимірювань?

3.               Як визначаються математичне сподівання та середньоквадратичне відхилення випадкової похибки результату непрямого вимірювання?