Практичне заняття №5
Тема: Оброблення результатів
прямих
багаторазових
рівноточних вимірювань
Мета: Освоїти методику оброблення
результатів прямих
багаторазових
рівноточних вимірювань
Теоретичні
відомості
Найпоширенішими
характеристиками матеріальних об’єктів та процесів є величини і
залежності між ними.
Якраз про них
створюється інформація за допомогою
засобів вимірювання. Вимірювання
є дуже різноманітними і кількість
їх різновидів зростає.
Виконавши процес
вимірювання, отримують результат
вимірювання, який не може бути абсолютно
точно рівний істинному значенню фізичної величини.
Причиною появи похибок є, з одного боку, недосконалість засобів вимірювання і неточність передачі робочим засобом вимірювання розмірів одиниць відповідних фізичних величин.
Недосконалість
засобів вимірювання проявляється як у випадкових, незакономірних вимірюваннях
результату при повторенні експерименту в однакових умовах, так
і в зміні результату вимірювання
внаслідок відмінності умов проведення експерименту, наприклад, зміни температури
навколишнього середовища, вологості
повітря, зовнішніх електричних чи
магнітних полів, напруги живлення мережі, наявності вібрацій і т. д.
З іншого боку, похибка вимірювання може бути обумовлена недосконалістю
методу вимірювання, що застосовується при даному вимірюванні. Так, наприклад, при вимірюванні характеристик
полів (наприклад,
температурного поля) внесення в поле датчика (в даному прикладі термометра), який має свої
певні характеристики (геометричний
розмір, масу, теплопровідність і т. д.), призводить
до зміни картини поля поряд з датчиком, а отже, фізична величина,
що
нас цікавить, даним методом
не може бути виміряна
абсолютно точно.
Отже, похибка результату
кожного вимірювання складається з багатьох складових, причиною
появи яких є різні фактори та джерела. Традиційний аналітичний підхід до оцінювання похибок результату складається з виділення цих складових, вивчення їх окремо і подальшого їх додавання. Знаючи властивості і оцінивши кількісні характеристики похибок вимірювання, можна правильно врахувати їх при оцінюванні похибки
результату чи, якщо це можливо, внести поправку
в результат вимірювання. Виділивши і оцінивши окремі складові похибок, іноді виявляється можливим організувати вимірювання так, щоб ці складові не вплинули на результат.
Таким чином, при
будь-якому
вимірюванні
існує похибка, яка є відхиленням результату
вимірювання
від істинного значення вимірюваної величини.
Пряме вимірювання – це вимірювання однієї фізичної величини, значення якої знаходять безпосередньо
без перетворення її роду
та використання відомих
залежностей.
Для реалізації
прямих вимірювань фізичної
величини Х необхідно
мати багатозначну міру з відповідним діапазоном зміни значень, чи однозначну
міру та масштабний
вимірювальний перетворювач.
Прямі багаторазові
вимірювання поділяються на рівно- та нерівноточні.
Рівноточними називаються вимірювання, що проводяться засобами вимірювання однакової точності за однією і тією ж методикою при незмінних зовнішніх умовах. При рівноточних вимірюваннях середнє квадратичне відхилення (СКВ) результатів всіх рядів вимірювань
рівні між собою.
Перед проведенням опрацювання результатів вимірювань необхідно переконатись в тому, що дані із вибірки, що оброблюється, статистично підконтрольні, групуються навколо одного і того
ж центра та мають однакову дисперсію. Стійкість змін часто оцінюють інтуїтивно на основі тривалих спостережень. Однак є математичні методи розв’язання поставленої задачі, так звані методи перевірки однорідності. Щодо вимірювань, то розглядається однорідність груп спостережень, необхідні ознаки якої полягають в оціненні незміщеності середніх арифметичних і дисперсій відносно один одного.
Перевірка допустимості різниці між оцінками дисперсій нормально розподілених результатів вимірювань виконується за допомогою критерія
Р.Фішера за наявності
двох груп спостережень і критерія М. Бартлетта, якщо груп більше.
Задача опрацювання результатів багаторазових вимірювань полягає в знаходженні оцінки вимірюваної величини та довірчого інтервала, в якому знаходиться її дійсне значення.
Вихідною інформацією для опрацювання є ряд із n (n>4) результатів вимірювань х1, х2,
х3,…, хn, з яких виключені відомі систематичні похибки, – вибірка. Число n залежить як від вимог до точності
результату, так і від реальної можливості
виконувати повторні зміни.
Послідовність опрацювання результатів прямих багатократних вимірювань складається з ряду етапів: визначення точкових оцінок закону розподілу результатів вимірювань. На даному етапі визначаються: середнє арифметичне значення вимірюваної величини; СКВ
результату вимірювання Sх; СКВ середнього арифметичного значення S![]() .
.
У ряді випадків для надійнішої ідентифікації закону
розподілу результатів
вимірювань можуть визначатись інші точкові оцінки:
- коефіцієнт асиметрії, ексцес і контрексцес, ентропійний коефіцієнт;
- визначення
закону розподілу результатів вимірювань або випадкових похибок вимірювань;
- оцінка закона
розподілу
за статистичними критеріями. При кількості спостережень n>50 для ідентифікації закону
розподілу
використовується критерій Пірсона або критерій Мізеса–Смірнова. При 50>n>15 для перевірки нормальності закону розподілу застосовується складений критерій, наведений в ГОСТ 8.207-76. При n<15 належність експерментального розподілу до нормального не перевіряється;
- визначення довірчих меж випадкової похибки. Якщо вдалося ідентифікувати закон розподілу результатів вимірювань, то з його використанням знаходять квантильний множник zp при заданому значенні
довірчої ймовірності Р.
В цьому випадку довірчі межі випадкової похибки визначаються як: ∆=
±Zp S![]() ;
;
- визначення меж невиключеної систематичної похибки θ результату вимірювань. Межі невиключеної систематичної похибки вважають рівними межам допустимих основних і додаткових похибок засобів вимірювання, якщо їх випадкові складові дуже малі. Довірча ймовірність при визначенні меж θ береться рівною довірчій ймовірності, що використовується при знаходженні меж випадкової похибки;
- визначення довірчих меж похибки результату вимірювання Δр. Така операція здійснюється
шляхом додавання СКВ випадкової
складової Sх і меж невиключеної систематичної складової θ залежно від
їх співвідношення;
- запис
результату вимірювання. Результат вимірювання записується у вигляді X = X ± ∆P при довірчій імовірності P=Pд.
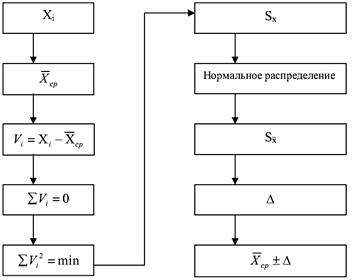
Рис. 1. Алгоритм оброблення результатів вимірювань
На рис. 1 зображені наступні позначення:
Хі – вимірювання;
Хср – середнє арифметичне результату
вимірювання;
Vі – випадкове відхилення результату
вимірювання;
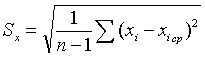 – середньоарифметичне відхилення кожного
результату вимірювання;
– середньоарифметичне відхилення кожного
результату вимірювання;
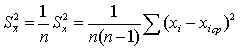 –
середньоквадратичне відхилення
величини Хср.
–
середньоквадратичне відхилення
величини Хср.
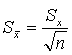 .
(1)
.
(1)
Результат вимірювання записується у
вигляді:
![]() . (2)
. (2)
![]() ,
(3)
,
(3)
де
tp – коефіцієнт стьюдента, який залежить від числа вимірювань n та довірчої
ймовірності Р.
Приклад
Проведено 12 вимірювань ємності
конденсатора та отримано наступні значення його ємності (див. таб. 1.):
Таблиця 1
Результати вимірювання ємності конденсатора.

Визначити з довірчою ймовірністю Р=0,95
інтервал, в якому знаходиться значення вимірювальної ємності.
Для n=12, Р=0,95
tp=2,18.
Розв’язання
![]()
![]() пФ.
пФ.
![]() пФ.
пФ.
![]() пФ.
пФ.
![]() пФ.
пФ.
Завдання
Цифровим вольтметром постійного струму
виконана серія прямих рівноточних вимірювань напруги. Провести оброблення
результатів цих вимірювань (табл. 2) з довірчою ймовірністю Р=0,95. Закон
розподілу результатів вимірювань вважати нормальним.
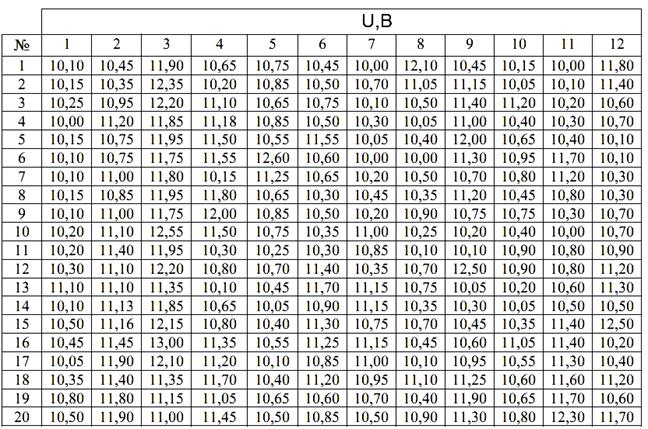
Таблиця 2
Результати вимірювання напруги цифровим вольтметром
Контрольні
запитання
1. Що являє собою пряме вимірювання?
3. Що являє собою рівноточне вимірювання?
4. У чому
полягає задача опрацювання результатів багатократних вимірювань?
5. Яким чином проводиться ідентифікація закону розподілу
вимірювальних величин?
6. Як визначається абсолютна похибка результату вимірювання
при багаторазових прямих рівноточних вимірюваннях?
7. Який алгоритм (послідовність дій) оброблення
результату вимірювання при багаторазових прямих рівноточних вимірюваннях?
8. Які точкові оцінки розподілу результатів багаторазових
вимірювань Вам відомі?
9. Яким чином представляється результат вимірювання при
багаторазових прямих рівноточних вимірюваннях?

