Практичне заняття №4

Тема: Виключення результатів вимірювань

 з грубими похибками

Мета: Освоїти методику виключення результатів

вимірювань з грубими похибками

 

Теоретичні відомості

Грубі похибки (промахи) відносяться до числа похибок, що змінюються випадковим чином при повторних вимірюваннях. Вони явно перевищують за своїм значенням похибки, виправдані умовами проведення експерименту.

Під промахом розуміється значення похибки, відхилення якого від центру розподілу істотно перевищує значення, виправдане об'єктивними умовами вимірювання. Тому з точки зору теорії ймовірності поява промаху малоймовірна. Причинами грубих похибок можуть бути неконтрольовані зміни умов вимірювань, несправність, помилки оператора та ін. Для виключення грубих похибок застосовують апарат перевірки статистичних гіпотез. У метрології використовуються статистичні гіпотези, під якими розуміють гіпотези про вид невідомого розподілу, або про параметри відомих розподілів.

Приклади статистичних гіпотез:

1) розглянута вибірка (або її окремий результат) належить генеральної сукупності;

2 ) генеральна сукупність розподілена за нормальним законом;

3 ) дисперсії двох нормальних сукупностей рівні між собою.

 У двох перших гіпотезах зроблено припущення про вид невідомого розподілу та приналежності окремих (підозрілих) результатів даному виду розподілу, а в третій – про параметри двох відомих розподілів. Поряд з висунутою гіпотезою розглядають і суперечливу їй гіпотезу. Нульовою (основною) називають висунуту гіпотезу. А конкуруючу (альтернативну) називають ту , яка суперечить нульовий. При висуванні та прийнятті гіпотези можуть мати місце такі чотири випадки:

1) гіпотеза приймається, причому і в дійсності вона правильна;

2) гіпотеза вірна , але помилково відкидається. Виникає при цьому помилку називають помилкою першого роду, а ймовірність її появи називають рівнем значущості і позначають q (α);

3) гіпотеза відкидається, причому в дійсності вона неправильна;

4) гіпотеза неправильна, але помилково приймається. Виникачу при цьому помилку називають помилкою другого роду, а ймовірність її появи позначають β. Величину 1- β, тобто ймовірність, що гіпотеза буде відкинута, коли вона помилкова, називають потужністю критерію.

Слід зауважити, що в нормативній документації по статистичному контролю якості продукції і підручниках з управління якістю ймовірність визнати непридатною партію придатних виробі (тобто, зробити помилку першого роду) називають "ризиком виробника", а ймовірність прийняти непридатну партію – "ризиком споживача".

Нульова статистична гіпотеза підтверджує приналежність перевірюваного "підозрілого" результату вимірювання (спостереження)  до цієї групи вимірювань. Формальним критерієм аномальності результату спостережень (а, отже, і підставою для прийняття конкуруючої гіпотези: "підозрілий" результат не належить даній групі вимірювань) при цьому служить межа, віднесена від центру розподілу на величину tS , тобто :

,                                                               (1)

де  – результат спостереження , що перевірявся на наявність грубої похибки;

      t – коефіцієнт, що залежить від виду та закону розподілу, об’єму вибірки, рівня значимості.

Таким чином, межі похибки залежать від виду розподілу, об’єму вибірки та обраної довірчої ймовірності.

При обробці вже наявних результатів спостережень довільно відкидати окремі результати не слід, так як це може призвести до фіктивного підвищення точності результату вимірювань. Група вимірів (вибірка) може містити кілька грубих похибок і їх виключення проводять послідовно, по одному. Всі методи виключення грубих похибок (промахів) можуть бути розділені на два основних типи:

а) методи виключення при відомому генеральному СКВ;

б) методи виключення при невідомому генеральному СКО.

Оскільки на практиці частіше зустрічаються вимірювання при невідомому СКО (обмежене число спостережень), у роботі розглянуті наступні критерії перевірки підозрілих (з точки зору похибок) результатів спостережень: Ірвіна, Романовського, варіаційного розмаху, Діксона, Смірнова та Шовене.

 

Завдання

Використовуючи правило 3 сігм, критерій Романовського, Ірвіна, варіаційного розмаху, Шовена та Смірнова встановити, чи є найбільший результат вимірювання твердості по 20 точкам на поверхні кільця роликопідшипника грубою похибкою. Результати вимірювань наведені в таблиці 1.

 

 

 

Таблиця 1

Варіант 1

Твердість, HRC

50.5

50.6

50.7

50.8

50.9

51

51.1

51.2

51.3

Частота, mi

1

2

4

5

4

2

1

0

1

Варіант 2

Твердість, HRC

55.5

55.6

55.7

55.8

55.9

56

56.1

56.2

56.3

Частота, mi

1

2

3

6

3

2

1

1

1

Варіант 3

Твердість, HRC

60.7

60.8

60.9

61.0

61.1

61.2

61.3

61.4

61.5

Частота, mi

2

2

3

5

4

1

1

1

1

Варіант 4

Твердість, HRC

40.6

40.7

40.8

40.9

41

41.1

41.2

41.3

41.4

Частота, mi

1

2

3

5

3

2

2

1

1

Варіант 5

Твердість, HRC

35.5

35.6

35.7

35.8

35.9

36

36.1

36.2

36.3

Частота, mi

2

1

3

6

3

2

1

1

1

Варіант 6

Твердість, HRC

58.1

58.2

58.3

58.4

58.5

58.6

58.7

58.8

58.9

Частота, mi

1

2

5

4

3

3

1

0

1

Варіант 7

Твердість, HRC

51.5

51.6

51.7

51.8

51.9

52

52.1

52.2

52.3

Частота, mi

1

1

6

5

3

2

1

0

1

Варіант 8

 

Твердість, HRC

64.5

64.6

64.7

64.8

64.9

70

70.1

70.2

70.3

Частота, mi

1

2

2

7

3

3

1

0

1

Варіант 9

Твердість, HRC

38.7

38.8

38.9

39

39.1

39.2

39.3

39.4

39.5

Частота, mi

1

1

5

6

3

1

1

1

1

Варіант 10

Твердість, HRC

47.1

47.2

47.3

47.4

47.5

47.6

47.7

47.8

47.9

Частота, mi

1

2

3

6

4

2

1

0

1

Варіант 11

Твердість, HRC

39.5

39.6

39.7

39.8

39.9

40

40.1

40.2

40.3

Частота, mi

1

2

4

5

4

1

1

1

1

Варіант 12

Твердість, HRC

42.1

42.2

42.3

42.4

42.5

42.6

42.7

42.8

42.9

Частота, mi

1

2

5

4

4

1

1

1

1

Варіант 13

Твердість,HRC

33.7

33.8

33.9

34

34.1

34.2

34.3

34.4

34.5

Частота, mi

1

1

4

6

4

2

0

1

1

Варіант 14

Твердість, HRC

72.1

72.2

72.3

72.4

72.5

72.6

72.7

72.8

72.9

Частота, mi

1

3

4

4

4

1

1

1

1

Варіант 15

Твердість,HRC

23.7

23.8

23.9

24

24.1

24.2

24.3

24.4

24.5

Частота, mi

1

1

4

5

5

2

0

1

1

 

 

 

Вихідні дані

Розглянемо приклад застосування критеріїв для виключення грубих похибок при вимірюванні швидкості ударної хвилі. Отримані результати представлені в таблиці 2.

Таблиця 2

Результати вимірювання швидкості ударної хвилі

Потрібно визначити, чи не містить результат спостереження V=3,50 км/с грубу похибку. Знаходимо оцінку  та S.

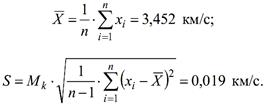
Проведемо вирішення задачі за допомогою за допомогою критеріїв, які встановлені для нормального розподілу.

Перевірка за критерієм 3ό

Знайдемо віддаленість підозріливого результату від центру розподілу:

 км/с.

Визначаєм межу похибки:  км/с.

Оскільки то можна зробити висновок, що результат V=3,50 км/с не містить грубої похибки.

Перевірка за критерієм Смірнова

З таблиці 4 (n<25) для прийнятого рівня значимості q=0,05 та об’єму вибірки n=20 знаходим значення коефіцієнта.

Наявність грубої похибки в результаті вимірювання V=3,50 км/с підтверджується, оскільки:

.

або                               .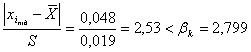

Перевірка за критерієм Романовського

Визначаєм характеристики розподілу без врахування підозріливого результату:                       , .

По таблиці знаходимо коефіцієнт Стьюдента при об’ємі вибірки k=n-1=19 та довірчій ймовірності Р=0,95;  t0,95=2,093.

Наявність грубої похибки підтверджується, оскільки:

.

 

Контрольні запитання

1.  Що являє собою груба похибка?

2.  Що являє собою критерій варіацяйного розмаху?

3.  Що являє собою правило 3 сігм?

4.  Що являє собою критерій Романовського та Діксона?

5.  Що являє собою критерій Шовене та Смірнова?