ТЕМА №8

сумісні вимірювання та оброблення їх результатів

План

1.   Характеристика сумісних вимірювань.

2.   Оброблення результатів сукупних вимірювань.

 

1. Характеристика сумісних вимірювань.

Сумісне вимірювання - непряме вимірювання, в якому значення декількох одночасно вимірюваних різнорідних величин отримують розв´язанням рівнянь, що пов´язують їх з іншими величинами, котрі вимірюються прямо чи опосередковано. Метою сукупних вимірювань є знаходження шляхом числових вимірювальних перетворень значень декількох різнорідних фізичних величин за неможливістю їхнього окремого прямого вимірювання.

2.  Оброблення результатів сумісних вимірювань. Оброблення результатів сумісних вимірювань полягає в знаходженні значень невідомих різнорідних величин та похибки їх результатів. Значення невідомих величин знаходять шляхом складання системи нормальних лінійних рівнянь та їх розв’язку з використанням головного та частинного визначника. Для оцінки точності результатів сукупного вимірювання слід обчислити їх середньоквадратичне відхилення.

У сумісних вимірюваннях величини х_і, що не піддаються безпосередньому спостереженню, визначаються за результатами вимірювань інших величин y_j, які є функціями:

                                      (1)

де і – порядковий номер невідомих величин х_і, і=1; 2; ... ; n; j – порядковий номер прямих вимірювань інших величин y_j, j=1; 2; … ; m.

Для випадку, коли функції  лінійні:

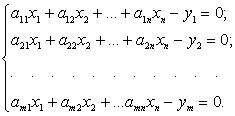                              (2)

Компактніше дана система матиме вигляд:

                                        (3)

індекси у коефіцієнтів а вказуються в послідовності “рядок – стовпчик”.

Ці рівняння замість точних значень Y_j містять результати їх вимірювань  із випадковими похибками . За m=n таку систему рівнянь можна розв’язати звичайними алгебраїчними прийомами, але точність визначення величини Х_і одноразовими прямими вимірюваннями Y_i буде невеликою. Щоб отримати вірогідніші результати обчислення Х_і, слід під час прямого вимірювання кожного значення Y_i виконати кілька спостережень, але тоді за  і наявності похибок  система стає алгебраїчно нерозв’язуваною.

Наприклад, під час дослідження залежності опору котушки від температури добуто такі результати (табл. 1):                                                          

                                                                                     Таблиця 1

t, 0C	Rt	t, 0C	Rt
20	R20	60	R60
30	R30	70	R70
40	R40	80	R80
50	R50

 

 

                                         

Функція  має вигляд:      .

Визначити опір R₀ котушки за температури 0 ⁰C, значення температурного коефіцієнта опору α та матеріалу дроту, яким намотано котушку.

Обробка результатів здійснюється в певній послідовності. Спочатку перетворимо формулу для R_t:

.

Тоді цю саму формулу можна записати так:

,

де а₁=1; х₁=R₀; a₂=t; х₂=αR₀; y=R_t.

Умовні рівняння (їхня кількість m) мають вигляд:

,

тобто

 

 

 

;

 

 

 

 

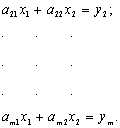
Система нормальних рівнянь має такий вигляд:

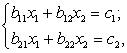
де:

;

;

;

;

.

Значення та можна знайти за допомогою визначників. Головний визначник системи:

.

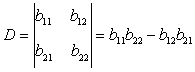Частинні визначники:

;

.

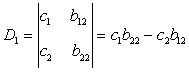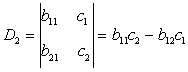Тоді

;   .

Підставивши значення та  в умовні рівняння, можна обчислити кінцеві похибки  для кожного з них за формулою:

.

Тоді середньоквадратичні відхилення результатів розв’язання даної системи нормальних рівнянь:

;     .

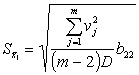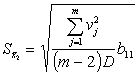Надійні межі випадкових похибок можна обчислити за формулами:

;     ;

коефіцієнт надійності t_γ (для m–n+1) взяти з таблиці 2.

Перший результат вимірювання:

.

Другий результат вимірювання:

.

Таблиця 2

Значення t_γ (для сукупних та сумісних вимірювань)

m–n+1	Р=0,95	Р=0,99
2	12,706	63,657
3	4,303	9,925
4	3,182	5,841
5	2,776	4,604
6	2,571	4,032
7	2,447	3,707
8	2,365	3,499
9	2,306	3,355
10	2,262	3,250

 

  Контрольні запитання

1.  Що являє собою сумісне вимірювання?

2. Яка послідовність оброблення результатів сумісних вимірювань?

3. Що являє собою головний визначник системи?

4. Що являє собою частинний визначник системи?

5. Як визначається результат сумісного вимірювання?

6. Як виражається похибка сумісного вимірювання?