Тема 5. Основні завдання і особливості теорії автоматичного керування

У лекції розглядаються основні завдання та особливості теорії автоматичного керування. Теорія автоматичного керування вивчає методи та принципи управління динамічними системами без безпосередньої участі людини. Завдання теорії включають аналіз і синтез систем управління, забезпечення стабільності, точності та швидкості реакції на зміни зовнішніх умов. Особливості теорії полягають у використанні математичних моделей для опису процесів і розробці алгоритмів, які дозволяють досягти оптимальних характеристик керування.

5.1. Статика САР. Умови статичної рівноваги і статичні характеристики ланок

Як зазначено раніше, завданням статики як розділу теорії автоматичного керування (ТАК) є вивчення систем автоматичного регулювання (САР) у статичному стані, який виникає після завершення перехідних процесів. Для того, щоб система перебувала в стані рівноваги, мають одночасно виконуватися такі умови (рис. 5.1):

1.     Збалансованість вхідних та вихідних сигналів — вхідний сигнал має бути пропорційним вихідному, що забезпечує стабільність і точність в роботі системи.

2.     Регулювання вихідної величини — система повинна здатна підтримувати вихідну величину на заданому рівні, коригуючи її відповідно до змін зовнішніх впливів або внутрішніх збурень.

3.     Відсутність коливань — після завершення перехідних процесів система повинна стабілізуватися без періодичних коливань, що можуть свідчити про нестабільність або погану настройку зворотного зв’язку.

4.     Виконання рівнянь рівноваги — для статичного стану система повинна задовольняти рівняння балансу між усіма впливами, що виникають у процесі її роботи.

Ці умови забезпечують стійкість та надійність системи в статичному режимі роботи.

Рисунок 5.1 – Умови статики САР

Основною характеристикою статики окремої ланки системи є регулювальна характеристика, яка показує залежність регульованої величини х від витрат робочого середовища Q:

x = f(Q) (5.1)

а основною характеристикою статики окремої ланки системи є характеристика вхід – вихід:

x_вих = f(х_вх) (5.2)

Важливим показником ланки є статичний коефіцієнт передачі:

(5.3)

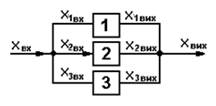
Результуюча статична характеристика паралельно з’єднаних ланок.

У теорії автоматичного регулювання паралельне з’єднання ланок передбачає, що вхідна величина подається одночасно на всі ланки, а загальна вихідна величина утворюється шляхом підсумовування вихідних значень кожної з цих ланок. Послідовне з’єднання ланок – це таке з’єднання, при якому вихідна величина попередньої ланки є вхідною для наступної (табл. 5.1):

Таблиця 5.2 – Схеми з’єднань ланок

Схеми з’єднань ланок
Паралельне з’єднання ланок	Послідовних з’єднань ланок
хвх = х1вх = х2вх = х3вх	Хвих = х1вих + х2вих + х3вих

5.2. Статична похибка і коефіцієнт передачі

Статична похибка — це відхилення регульованої величини від заданого значення, яке спостерігається після завершення перехідного процесу, коли система досягає стабільного стану. Цей показник є важливим критерієм для оцінки якості роботи системи автоматичного регулювання (САР), оскільки він відображає точність системи в стаціонарному режимі.

Чим менша статична похибка, тим вища стабільність і ефективність системи. Це має велике значення, зокрема, у таких сферах, як промислове виробництво, енергетика, хімічна і харчова промисловість, де точне підтримання параметрів, наприклад, температури, тиску чи рівня, є критично важливим для забезпечення безпеки, якості продукції та ефективності роботи обладнання. Тому мінімізація статичної похибки є важливою для забезпечення стабільності та надійності систем автоматичного керування.

Вважатимемо, що головного зворотного зв’язку в системі немає (САК знаходиться в розімкнутому стані), схема зображена на рисунку 5.2.

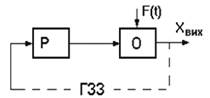
Рисунок 5.2 — Схема САК зі головним зворотнім з’язком:

P – регулятор, який формує керуючий сигнал на основі відхилення вихідного параметра; O – об'єкт керування, тобто система або процес, яким потрібно керувати; F(t) – зовнішнє збурення, яке впливає на об'єкт (наприклад, навантаження, температурні коливання тощо); Xвих – вихідний сигнал системи, який контролюється; ГЗЗ (глобальний зворотний зв’язок) – механізм, що повертає інформацію про вихідний параметр для корекції керуючого сигналу.

Тоді при початковому значенні збурення f₀(t) вихідна величина об’єкта х_0вих відповідатиме потрібному значенню регульованої величини. Зміна збурення до значення f₁(t) призведе до зміни вихідної величини об’єкта до значення х_1вих і появи відхилення при розімкнутому стані системи Δх = х_0вих – х_1вих

Якщо замкнути систему за допомогою ГЗЗ, то в замкнутій системі регулятор Р діятиме на зменшення відхилення Δх (в ідеальному випадку до нуля).

Проте регулятор не в змозі повністю ліквідувати Δх. Частина Δх, яка залишається в замкнутій системі, є статичною похибкою замкнутої системи.

Δ = Δх – Δх_вих (5.4)

Величина Δ знову надходить на вхід об’єкта, тому можна записати

Δ = Δх_вх (5.5)

Розділивши всі члени рівняння (5.4 на величину Δ і врахувавши (5.5), отримаємо

Оскільки Δх_вих / Δх_вх =К – коефіцієнт передачі(підсилення) розімкнутої системи, то статичну похибку замкнутої системи запишемо у вигляді:

(5.6)

З цієї формули можна зробити такі висновки:

1.   Статична похибка замкнутої системи визначається як стала різниця між заданим значенням регульованої величини та її фактичним значенням у режимі усталеного руху. Вона прямо пропорційна відхиленню регульованої величини в розімкнутій системі (тобто без зворотного зв’язку) і обернено пропорційна коефіцієнту підсилення розімкнутої системи. Це означає, що чим більше підсилення у системі в відкритому контурі, тим менша статична похибка в замкнутому контурі. Така залежність свідчить про те, що більший коефіцієнт підсилення покращує точність регулювання та зменшує похибку.

2.   У розімкнутій системі величина відхилення Δx прямо залежить від збурень F(t), які діють на об’єкт керування. Оскільки зворотний зв’язок у замкнутій системі лише частково компенсує вплив зовнішніх збурень, статична похибка в замкнутій системі також залежить від величини й характеру збурення. Якщо збурення значні або швидко змінюються, система може не встигати їх повністю компенсувати. Це призводить до збільшення похибки, що може негативно вплинути на точність регулювання. Таким чином, здатність системи компенсувати збурення залежить від її підсилення та швидкості реагування.

5.3. Динаміка систем автоматичного регулювання

Динамічні властивості лінійної системи автоматичного регулювання (САР) можна детально аналізувати за допомогою диференційного рівняння, яке описує поведінку замкнутої САР. Це рівняння отримується на основі рівнянь, що описують ланки системи, включаючи елементи, такі як передавачі, регулятори, зворотний зв'язок і інші компоненти.

Зазвичай рівняння замкнутої САР формується шляхом об'єднання рівнянь, які описують кожну ланку, враховуючи їхні характеристики, а також зворотний зв'язок. Для лінійної системи такого типу можна застосовувати методи математичного моделювання, наприклад, методи Лапласа або частотного аналізу, що дозволяють отримати загальне рівняння, яке описує динамічні характеристики системи в часі або в частотній області.

Рівняння замкнутої системи має вигляд, що поєднує вплив вхідного сигналу, параметрів кожної ланки та зворотного зв’язку. Цей аналіз дозволяє вивчати такі важливі динамічні характеристики, як час встановлення, амплітудно-частотну характеристику, стійкість, перехідні процеси, а також оцінювати ефективність та точність роботи системи автоматичного регулювання.

Направленість впливу ланок у системі забезпечується завдяки використанню детектуючих ланок, які здатні передавати енергію лише в одному напрямку.

Методика знаходження рівнянь САР (рис.5.3):

Рисунок 5.3 – Послідовність складання рівняння динаміки

5.4. Форми запису рівнянь динаміки.

Рівняння динаміки ланок і систем автоматичного керування (САК) можуть бути складені так само, як і рівняння статики, але з урахуванням часу та змін у динамічному процесі. Це може бути зроблено в абсолютних величинах, відхиленнях або відносних величинах, в залежності від способу моделювання і бажаного рівня абстракції.

Для запису рівнянь динаміки систем часто використовують операторну форму представлення диференціальних рівнянь, в якій замість похідних та інтегралів застосовуються спеціальні оператори, що визначаються через оператор «р». Оператор p є математичним символом, що замінює звичайні похідні. Він визначається як:

(5.9)

Тоді

(5.10)

записуємо інтеграли в операторній формі:

(5.11)

При операторній формі запису оператор „p” розглядається, як деяка величина, на яку можуть поширюватись всі алгебраїчні дії.

Правомірність відокремлення функції від знака оператора можна показати на основі відомих положень математики.

Наприклад, на основі того, що похідна суми деяких величин x, y, z, є сума цих похідних:

(5.12)

В операційній формі можна записати:

(5.13)

Множення або ділення обох частин деякого рівняння на оператор «р» можливе, тому що, можливе почленне диференціювання або інтегрування обох сторін рівностей.

Питання для самоперевірки

1.   Що таке статична похибка в системах автоматичного регулювання?

2.   Як визначається коефіцієнт статичної похибки в САР?

3.   Що таке коефіцієнт передавальної здатності системи (K)?

4.   Які типи похибок можна зустріти в системах автоматичного регулювання?

5.   Як зміна коефіцієнтів системи впливає на похибки регулювання?