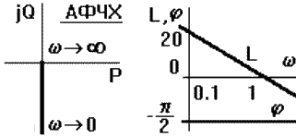Практична робота 5

Тема: Дослідження частотних характеристик ланок.

Мета: ознайомитись з частотними характеристиками типових ланок та провести дослідження із застосуванням до САК

 

Якщо подати на вхід системи з передаточною функцією W (p) гармонійний сигнал

 

                                    (1)

,

то після завершення перехідного процесу на виході встановляться гармонійні коливання

 

                                                (2)

 

з тією ж частотою, але іншими амплітудою і фазою, залежними від частоти збурюючого  впливу. За ним можна судити про динамічні властивості системи. Залежності, що зв'язують амплітуду і фазу вихідного сигналу з частотою вхідного сигналу, називаються частотними характеристиками (ЧХ). Аналіз ЧХ системи з метою дослідження її динамічних властивостей називається частотним аналізом.

W (j), Що дорівнює відношенню вихідного сигналу до вхідного при зміні вхідного сигналу по гармонійному закону, називається частотною передаточною функцією. Легко помітити, що вона може бути отримана шляхом простої заміни p на j в виразу W (p).

W (j) Є комплексна функція, тому

 

                                        (3)

Де  P ()- дійсна ЧХ; Q ( - уявна ЧХ; А () - амплітудна ЧХ (АЧХ).

Маючи комплексну функцію, можна визначити() - фазову ЧХ (ФЧХ). АЧХ дає відношення амплітуд вихідного і вхідного сигналів, ФЧХ - зсув по фазі вихідної величини щодо вхідної:

                                                  (4)

   

                                                            (5)

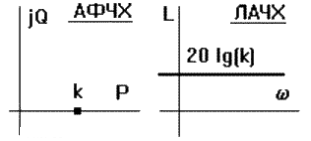
Якщо W (j) Зобразити вектором на комплексній площині, то при зміні  від 0 до +  його кінець буде викреслювати криву, яка називається годографом вектора W (j), Або амплітудно-фазову частотну характеристику (АФЧХ) (рис.1).

 

Рисунок 1 – Графік амплітудно-фазової частотної характеристики

 

Гілку АФЧХ при зміні  від -  до 0 можна отримати дзеркальним відображенням даної кривої відносно дійсної осі.

У теорії автоматичного управління (ТАУ) широко використовуються логарифмічні частотні характеристики (ЛЧХ) (рис. 2): логарифмічна амплітудна ЧХ (ЛАЧХ) L () і логарифмічна фазова ЧХ (ЛФЧХ) (). Вони виходять шляхом логарифмування передавальної функції:

 

       (6)

 

ЛАЧХ отримують з першого доданка, яке з міркувань масштабування множиться на 20, і використовують не натуральний логарифм, а десятковий, тобто L () = 20lgA (). Величина L () Відкладається по осі ординат в децибелах. Зміна рівня сигналу на 10 дб відповідає зміні його потужності в 10 разів. Так як потужність гармонійного сигналу Р пропорційна квадрату його амплітуди А, то зміни сигналу в 10 разів відповідає зміна його рівня на 20 дб, так як              lg (P2 / P1) = lg (A22 / A12) = 20lg (A2 / A1).

 

 

 

 

 

 

 

 

 

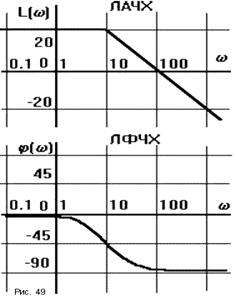
Рисунок  2 – Логарифмічні частотні характеристики

 

По осі абсцис відкладається частота w в логарифмічному масштабі. Тобто одиничним проміжкам по осі абсцис відповідає зміна w в 10 разів. Такий інтервал називається декадою. Так як lg (0) = -, То вісь ординат проводять довільно.

ЛФЧХ, що отримується з другого доданка, відрізняється від ФЧХ тільки масштабом по осі . Величина() Відкладається по осі ординат в градусах або радіанах. Для елементарних ланок вона не виходить за межі: - + .

ЧХ є вичерпними характеристиками системи. Знаючи ЧХ системи, можна відновити її передавальну функцію і визначити параметри.

Типові ланки. Знаючи передавальну функцію ланки W (p), легко отримати всі його частотні характеристики. Для цього необхідно підставити в передавальну функцію j замість p, отримаємо АФЧХ W (j). Потім треба висловити з неї ВЧХ P () і МЧХ (Q (). Після цього перетворимо АФЧХ в показову форму і отримуємо АЧХ A () і ФЧХ (), а потім визначаємо вираз ЛАЧХ L (w) = 20lgA () (ЛФЧХ відрізняється від ФЧХ тільки масштабом осі абсцис).

1.      Безінерційна ланка.

Передавальна функція: W (p) = k.

АФЧХ: W (j) = к.

ДЧХ: P () = к.

УЧХ: Q () = 0.

АЧХ: A () = K.

ФЧХ: () = 0.

ЛАЧХ: L () = 20lgk.

Деякі ЧХ показані на рис. 3.

 

 

 

Рисунок 3 – Характеристики без інерційної ланки

 

2.      Інтегруюча ланка. Передавальна функція: W (p) = k / p.

Розглянемо окремий випадок, коли k = 1, тобто W (p) = 1 / p.

АФЧХ: .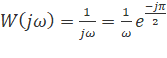

ДЧХ: P () = 0.

УЧХ: Q () = - 1 /.

АЧХ: A () = 1 /.

ФЧХ: () = - / 2.

ЛАЧХ: L () = 20lg (1 /) = - 20lg ().

ЧХ показані на рис. 4.

 

 

Рисунок 4 – Характеристики інтегруючого ланки

 

3.      Аперіодична ланка. При k = 1 одержуємо наступні вирази ЧХ:

;

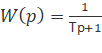ДЧХ: ;

УЧХ: ;

ФЧХ: () = 1 - 2 = - arctg (T);

АЧХ: ;

ЛАЧХ: L () = 20lg (A ()) = - 10lg (1 + (T) 2).

 

ЛФЧХ, АФЧХ показані на рис. 5.

 

 

Рисунок 5 – Характеристики аперіодичної ланки

 

4.      Інерційні ланки другого порядку. При k = 1 передавальна функція ланки:

.

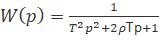Зважаючи на складність виведення виразів для частотних характеристик розглянемо їх без доказу, вони показані на рис. 6.

 

 

 

Рисунку 6 – Характеристики інерційної ланки другого порядку

 

 

Завдання до виконання

Провести побудову частотних характеристик для ланок, що вказані в структурній схемі (рис. 7) та охарактеризувати.

           

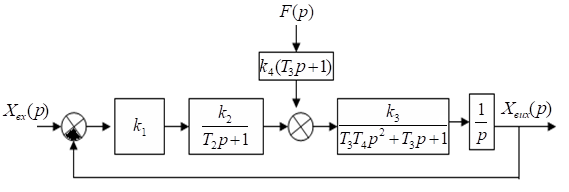
Рисунок 7 –     Структурна схема САР

 

 

Таблиця 1 – Варіанти завдань

                                            

№

К1

К2

К3

К4

Т1

Т2

Т3

Т4

1

1,53

0,8

1,3

2

1,1

0,15

0,1

0,043

2

2,60

2,4

0,8

3,1

5,2

2,1

0,35

0,025

3

1,53

0,8

1,3

2,15

6,4

3,7

0,12

0,043

4

1,14

2,4

0,8

4,8

0,8

8,4

0,35

0,043

5

2,30

2,9

0,8

0,5

1

0,9

0,45

0,018

6

 

0,3

0,9

0,85

1,2

4,2

0,18

0,16

0,8

7

 

2,1

1,3

0,9

3

4,1

1,2

0,8

0,05

8

 

1,4

2,1

0,8

2,4

3,3

0,2

0,11

0,028

9

 

1,5

0,8

1,4

2

5,5

3

0,15

0,019

10

 

2,2

2,6

1,2

5

2,4

3,1

0,13

0,9