Тема 13. Наближені методи оцінки якості

У темі "Наближені методи оцінки якості" вивчаються спрощені підходи до аналізу динамічних характеристик систем автоматичного керування, зокрема стійкості, точності та перехідних процесів.

13.1. Кореневі методи оцінки якості

До даного виду методів належать:

1.            Оцінка якості по розміщенню коренів на комплексній площині;

2.            Аналіз за допомогою діаграми зон параметрів;

3.            Кореневий годограф.

Якість системи можна оцінювати за розташуванням коренів на комплексній площині, використовуючи різні критерії. Одним із таких методів є аналіз за найменшим коренем, тобто коренем, який розташований найближче до уявної осі комплексної площини коренів (див. рис. 13.1).

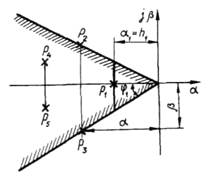
Рисунок 13.1 – Розміщення комплексних коренів

Якщо найменший дійсний корінь , то аперіодична ступінь стійкості системи дорівнює . Якщо найближче до вертикальної осі розміщуватиметься пара комплексних коренів , то ступінь стійкості називають коливальним.

Коливальність системи в цьому разі:

(13.1)

Метод приблизного знаходження мінімального кореня полягає в такому:

1.                 На комплексній площині визначаються всі корені характеристичного рівняння системи.

2.                 Вибирається корінь, який має найменшу відстань до уявної осі (тобто найменше абсолютне значення дійсної частини).

Рисунок 13.2 – Знаходження найменшого кореня

3.     Для оцінки відстані можуть використовуватися числові методи або графічний аналіз на комплексній площині. Алгоритм пошуку передбачає таку послідовність:

–             знаходять мінімальне значення кореня за умови, що за час величина відхилення регульованої величини x від її початкового значення , буде дорівнювати ;

–                   цю вимогу можна виконати, якщо найменша дійсна частина кореня характеристичного рівняння замкнутої системи не буде меншою за деяку величину .

(13.2)

–                   виконують перевірку “мінімальності” знайденого за формулою (13.2) кореня в умовах даної системи.

–                   у новій системі координат (після переміщення вертикальної осі) характеристичне рівняння замкнутої системи матиме вигляд:

(13.3)

–                   якщо нова система з характеристичним рівнянням (*) буде нестійкою, то це означає, що визначений за заданими умовами якості системи мінімальний корінь в дійсності не є мінімальним. Тому в даній системі неможливо виконати поставлену умову . В цьому випадку змінити її відносно знайти відповідне нове значення мінімального кореня і перевірити його мінімальність.

4.                 Цей корінь вважається мінімальним і використовується для оцінки якості системи, наприклад, її стійкості чи швидкості затухання перехідних процесів.

13.2. Частотні методи оцінки якості САР

Частотні методи досліджування, які дістали найбільше поширення на практиці, базуються на математичній залежності характеристики перехідного процесу x(t) від дійсної частотної характеристики замкнутої системи за збуренням .

В основу доведення цієї залежності лежить відоме положення, що будь-яку періодичну обмежену дійсну функцію, яка має скінченну кількість розривів і екстремумів, можна розкласти в нескінченний ряд синусоїдальних функції – ряд Фур’є.

При доведенні функціональної залежності виходять з того, що в системі діє збурення у вигляді одиничного кидка збурення (од. імпульсна ф-ція або ф-ція Дірака), яке розкидається в ряд Фур’є.

Дійсну частотну характеристику замкнутої системи за збуренням знаходять з виразу відповідної передаточної функції замкнутої системи , де - передаточна функція об’єкту за збуренням; - передаточна функція розімкнутої системи. Після підстановки у вираз дістанемо амплітудно-фазову частотну характеристику замкнутої системи за збуренням:

(13.4)

де - відповідно уявна і дійсна частотні характеристики замкнутої системи за збуренням.

Практично розгляд характеристики обмежується зоною суттєвих частот .

Під зоною суттєвих частот розуміють зону зміни частоти від 0 до , в якій виконується умова (при ця умова не порушується).

В зоні суттєвих частот виконується апроксимація характеристики , яку замінюють рівнозначними фігурами - трапеціями і трикутниками.

При заміні в зоні суттєвих частот мають виконуватись такі правила:

1.         Прямолінійні частини фігур мають по можливості точно збігатися з кривою .

2.                 Всі n фігур (трапеції і трикутники) повинні мати однією зі своїх сторін вертикальну вісь.

3.         Алгебраїчна сума площ всіх n фігур, якими замінюють характеристику має дорівнювати площі, обмеженій характеристикою .

4.                 Кількість фігур n має бути по можливості менша.

Після заміни рівнозначними фігурами обмежуючись розглядом інтеграла в зоні суттєвих частот:

(13.5)

З цієї формули робимо висновок, що ординату перехідного процесу можна дістати як величину, пропорційну сумі площ (інтегралів) еквівалентних фігур.

13.3. Аналіз якості за допомогою діаграм зон параметрів

Характерним прикладом цієї групи методів може бути розширена діаграма Вишнеградського, яка будується на основі розглянутої раніше діаграми при вивченні критерію стійкості Вишнеградського.

На розширеній діаграмі виділяються чотири зони: , які відповідають різним виглядам коренів і їх розміщенню відносно вертикальної осі в комплексній площині коренів (рис.13.3)

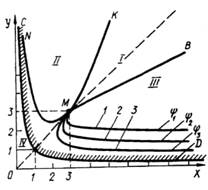
Рисунок 13.3 – Розширена діаграма Вишнеградського

Зона - умову . Її межею є рівнобічна гіпербола , рівняння якої , де - параметри Вишеградського. Цій зоні, яка є зоною нестійкого стану системи. Зони в площині є зонами стійкого стану системи. На графіках покажемо, як розміщення коренів впливає на форму перехідного процесу.

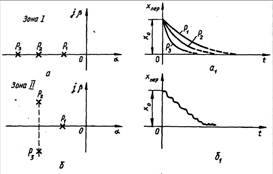
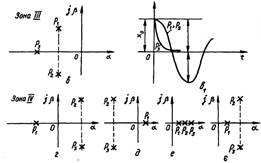
Рисунок 13.4 – Розміщення коренів та перехідних характеристик

Зона , межа якої КМВ є зоною аперіодичних процесів. Їй відповідають від’ємні дійсні корені характеристичного рівняння системи третього порядку . Умова знаходження коренів у даній зоні має вигляд:

(13.6)

Зона , межа якої KMN відокремлює зону монотонних процесів б, б1 Ближчим до вертикальної осі є дійсний корінь . Рівняння межі зони має вигляд:

(13.7)

Розміщення коренів і вигляд перехідного процесу в зоні , межа якої ДMB показано на рисунку. в, в_1. Тому, що дійсний корінь розміщується далі від вертикальної осі, характер перехідного процесу коливальний.

Умова знаходження коренів у зоні має вигляд:

(13.8)

Питання для самоперевірки

1.     Що розуміють під наближеними методами оцінки якості систем?

2.     Яку роль відіграє перехідна характеристика у наближеній оцінці якості?

3.     Які основні параметри якості аналізуються при наближених методах?

4.     У чому полягає суть логарифмічних частотних характеристик при оцінці якості?

5.     Як впливають запас за фазою і запас за амплітудою на якість системи?