Тема 10. Частотні
критерії стійкості
Частотні критерії стійкості використовуються для аналізу стійкості
систем автоматичного керування на основі їх частотних характеристик. До таких
критеріїв належать методи Найквіста,
Михайлова та критерію Боде. Вони
ґрунтуються на побудові графіків амплітудно-фазових характеристик відкритої
системи для визначення умов стійкості. Частотні критерії дозволяють оцінити, чи
система залишатиметься стабільною при зміні частоти вхідного сигналу, що робить
їх ефективними для аналізу систем з запізненням та у складних динамічних
умовах.
10.1. Частотні критерії стійкості критерій Михайлова
Критерій
Михайлова — це частотний метод аналізу стійкості лінійних систем автоматичного
керування (САК), який дозволяє оцінити стійкість системи на основі її
амплітудно-фазової характеристики або годографа в комплексній площині.
Ось як
виконується оцінка стійкості за критерієм Михайлова:
1. Визначаємо характеристичне рівняння
замкнутої системи:
D(р)=a0pn + аn-1pn-1+ ... +an-1p+an (10.1)
2. Здійснюємо заміну p на jω:
D(jw)=a0(jw)n+a1(jw)n-1+…+an-1(jw)+an (10.2)
3. Обчислити дійсну та уявну частини
характеристичного рівняння: дійсну А(w) і уявну В(w):
D (jw) = А(w)+ j В(w)
(10.3)
4. Здійснюємо побудову годографа
Михайлова, підставляючи значення ω від 0 до ∞. По горизонталі
відкладається дійсна частина, по вертикалі — уявна (рис. 10.1)
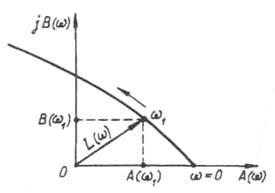
Рисунок 10.1 – Годографа Михайлова
5.
Аналіз напрямку та кількості обертів годографа:
1) Напрямок обертання годографа: Годограф повинен обертатися проти годинникової стрілки. Це
означає, що при збільшенні частоти (ω\omegaω)
амплітудно-фазова характеристика повинна рухатися в напрямку проти годинникової
стрілки в комплексній площині.
2) Кількість обертів: Годограф має зробити точно n/2n/2n/2 повних обертів навколо початку координат, де nnn
— порядок системи (кількість полюсів передавальної функції). Якщо система має
вищий порядок, кількість обертів збільшується пропорційно.
6.
Висновок щодо стійкості системи:
1) Стійка система: Система вважається стійкою, якщо годограф Михайлова:
– проходить через правильні квадранти;
– робить рівно n/2 повних обертів
навколо початку координат і рухається проти годинникової стрілки.
2) Нестійка система: Якщо обертів
годографа менше або більше, або напрямок обертання відрізняється (наприклад,
годограф обертається за годинниковою стрілкою), то система нестійка.
Переваги критерію Михайлова:
1. Швидкий аналіз: Критерій дозволяє швидко оцінити стійкість системи без
необхідності розв'язувати характеристичне рівняння.
2. Зручність: Застосування цього методу не вимагає складних обчислень, що
особливо корисно при необхідності швидко перевірити поведінку системи.
Цей підхід ідеально
підходить для систем, де необхідно провести оцінку стійкості при частотному
аналізі, і дає змогу одразу побачити, чи знаходяться полюси в стабільній
частині комплексної площини.
10.2. Дослідження стійкості за допомогою побудови зон стійкості
(метод D-розбиття)
Метод D-розбиття є
важливим інструментом для аналізу стійкості систем автоматичного керування
(САК) при зміні одного або кількох параметрів. Це ефективний підхід для
вивчення впливу варіацій параметрів на стійкість системи, особливо коли точні
аналітичні розрахунки ускладнюються через
великий порядок рівнянь.
Суть методу D-розбиття:
Метод полягає в визначенні областей стійкості в
просторі параметрів. Це означає, що за допомогою цього методу
можна знайти зони, в яких зміни одного або двох параметрів системи не
призводять до її нестійкості. Задача полягає в тому, щоб виявити такі ділянки в
параметричному просторі, де система залишається стабільною, навіть при
коливанні значень параметрів.
Процес застосування методу D-розбиття:
1. Визначення параметрів:
Першим кроком є визначення, які параметри (наприклад, коефіцієнти підсилення,
часи затримки чи інші характеристики ланок) можуть впливати на стійкість
системи.
2. Побудова простору параметрів:
Далі будують простір параметрів, де для кожного набору значень параметрів
визначається стійкість системи.
3. Аналіз стійкості:
Для кожного набору значень параметрів перевіряється стійкість системи. Це можна
зробити за допомогою раніше розглянутих критеріїв, таких як критерії Рауса—Гурвіца
чи Михайлова.
4. Визначення зони стійкості:
Визначаються ті області простору параметрів, де система залишається стійкою. Це
можуть бути певні діапазони значень параметрів, що забезпечують стабільну
роботу системи.
5. Оформлення результатів:
Результати аналізу часто зображаються
графічно у вигляді контурів або областей, що відображають зони стійкості в
просторі параметрів.
Переваги методу D-розбиття:
1. Зручність для багатопараметричних
систем: Метод дозволяє ефективно вирішувати завдання з багатьма
змінними параметрами, де інші методи аналізу можуть бути надто складними або
громіздкими.
2. Застосування до реальних систем: Дозволяє виявити ті
параметри системи, зміна яких може привести до її нестабільності, що критично
важливо при проєктуванні складних автоматичних
систем.
3. Оцінка на діапазонах: На відміну від
аналітичних методів, які часто орієнтовані на точні значення, цей метод працює
з діапазонами, що дає більшу гнучкість у роботі з реальними умовами.
Метод D-розбиття є потужним інструментом для підтримки
проектування стабільних САК, дозволяючи врахувати варіації параметрів і
забезпечити стійкість в широкому діапазоні умов.
Метод базується на характеристичному рівнянні системи, у якому
один або кілька коефіцієнтів розглядаються як змінні параметри. Для визначення
меж зон стійкості рівняння розв’язують відносно цих параметрів при критичних
значеннях (наприклад, коли корені рівняння мають нульові або чисто уявні
значення). В результаті отримують границі D-областей, що розділяють стійкі та
нестійкі режими роботи.
D-розбиття по одному параметру. Розглянемо
методику побудови зони стійкості в площині комплексного параметра Тx
1. Вихідне характеристичне рівняння D (р)
= 0 представимо у вигляді
Х(р) + ТxУ(р) = 0
(10.4)
Знаходимо величину
досліджуваного параметра: Tx =-X(p)/Y(p)
2. Знаходимо комплексний вираз параметра Тx,
використовуючи заміну р = jw, і виділимо його
дійсну і уявну складові: Тх = А(w)+jB(w).
Тx
становить деяку криву в комплексній площині, яка відповідає уявним кореням
характеристичного рівняння і є сукупністю параметрів Тх,
при яких система знаходиться на межі cтійкості. Така
характеристика називається межею стійкості в площині параметра D, або кривою
D-розбиття.
3. В комплексній площині параметра D за
правилом штриховки Неймарка знаходимо
зону стійкості.
«Правило штриховки формулюють
так: якщо рухатись по межі D-розбиття від значень w = -![]() до значень w = +
до значень w = + ![]() , то зона стійкості буде розташована зліва від межі стійкості (це
аналогічно тому, що якщо в комплексній площині коренів характеристичного
рівняння рухатись вздовж вертикальної (уявної) осі, яка є межею стійкості в
площині коренів від -
, то зона стійкості буде розташована зліва від межі стійкості (це
аналогічно тому, що якщо в комплексній площині коренів характеристичного
рівняння рухатись вздовж вертикальної (уявної) осі, яка є межею стійкості в
площині коренів від -![]() до +
до + ![]() , то зона стійкості знаходитиметься зліва від вертикальної осі)» [6].
, то зона стійкості знаходитиметься зліва від вертикальної осі)» [6].
4. Задаючи запас стійкості в зоні,
обмеженій кривою D-розбиття, виділимо на дійсній (горизонтальній) осі (бо
параметр Тx
є дійсною, фізично реальною величиною) необхідний, робочий діапазон значень
параметра Тx
,який може бути рекомендовано при проектуванні і настроюванні відповідної
системи.
Цей метод особливо корисний для проєктування
систем керування, оскільки дозволяє знаходити допустимі діапазони параметрів,
за яких система залишається стійкою.
10.3. Критерії стійкості Найквіста
Особливістю критерію Найквіста є те, що
він дає змогу: оцінювати динамічні властивості замкнутих систем по частотних
характеристиках відповідних розімкнутих систем; досліджувати динамічні
властивості замкнутої системи при відсутності рівнянь динаміки систем або
окремих елементів.
У цьому разі достатньо мати експериментальні частотні
характеристики системи або відповідних ланок, які можуть бути визначені на
реальних елементах системи або на їх моделях.
При відсутності математичного описання ланок (або й системи в
цілому) цей критерій є незамінним для дослідження динамічних процесів в
системах регулювання. Водночас він дещо складніший за розглянуті раніше.
Для оцінки стійкості системи за критерієм Найквіста
виконують таку послідовність дій:
1. Спочатку визначають розімкнену
передавальну функцію системи W(s) і підставляють у неї s=jω,
щоб отримати частотну характеристику.
2. Далі будують годограф Найквіста,
відкладаючи на комплексній площині дійсну та уявну частини функції W(jω)
при зміні частоти ω від нуля до нескінченності та назад (рис. 10.3):
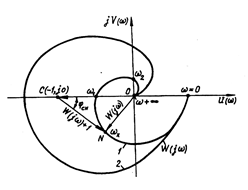
Рисунок 10.3 – АФХ
3. Потім визначають кількість полюсів
розімкненої системи, що знаходяться в правій півплощині комплексної площини, і
позначають її як p. Далі обчислюють, скільки разів і в якому напрямку годограф
обійшов точку −1+j0, і позначають це число як n. Оберт вважається
позитивним, якщо він відбувається проти годинникової стрілки.
«Умови стійкості розімкнутої системи: якщо розімкнута система САК
є стійкою, то для стійкої замкнутої системи необхідно і достатньо, щоб АФХ
розімкнутої системи не охоплювала точку з координатами (-1;j0) при зміні
частоти від 0 до ![]() » [2].
» [2].
Питання для
самоперевірки
1. Що таке
частотні критерії стійкості та в чому полягає їх значення для аналізу систем
автоматичного керування?
2. Як
критерій Михайлова використовується для аналізу стійкості системи в частотній
області? Опишіть, як побудувати годограф Михайлова.
3. Що таке
амплітудно-фазова характеристика, і як її використовують для оцінки стійкості
системи автоматичного керування?
4. Яке
значення має частотний критерій стійкості для визначення запасу стабільності
системи?