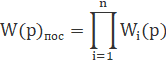Тема 8. Передаточні функції та частотні
характеристики
У лекції розглядаються передаточні
функції та частотні характеристики систем автоматизованого управління. Передаточна
функція описує математичний зв'язок між вхідними та вихідними сигналами
лінійної системи в частотній області, що дозволяє легко аналізувати її
поведінку за допомогою алгебраїчних рівнянь. Частотні характеристики, у свою
чергу, визначають, як система реагує на сигнали різних частот, і включають
амплітудно-частотну та фазо-частотну характеристики. Вивчення цих характеристик
дає можливість оцінити стійкість, точність і швидкість реакції системи на
зовнішні впливи.
Основною частотною
характеристикою є амплітудно-фазова характеристика (АФЧХ, АФХ). Її можна
дістати двома способами: аналітичним і експериментальним.
Для побудови АФХ
графоаналітичним методом у вираз відповідної передаточної функції роблять
підстановку
р = jω,
де ![]() ω – частота, що може змінюватись від –∞
до +∞.
ω – частота, що може змінюватись від –∞
до +∞.
У загальному випадку АФХ має вигляд:
![]()
(8.1)
Оскільки W(jω) –
комплексна величина, то її можна записати, виділяючи дійсну u(ω) та уявну
v(ω) частини, у вигляді:
W(jω) = U(ω)
+ jV(ω),
(8.2)
де U(ω), V(ω) – відповідно дійсна і
уявна частини характеристики.
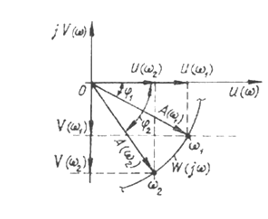
Рисунок 8.1 –
Амплітудно-фазова характеристика
У комплексній площині,
якщо відомі вирази u(ω) і v(ω) можна побудувати відповідні
характеристики.
Характеристику ![]() називають амплітудно-частотною
характеристикою, а залежність
називають амплітудно-частотною
характеристикою, а залежність ![]() – фазочастотною.
– фазочастотною.
Всі частотні
характеристики можуть бути побудовані в логарифмічному масштабі. У цьому
випадку їх називають логарифмічними частотними характеристиками.
Відповідно до вище
вказаного матеріалу АЧХ та ФЧХ для ланок наступні (табл. 8.1).
Таблиця 8.1 –
Характеристики ланок

8.1. Послідовне
з'єднання ланок
При послідовному з’єднанні ланок вихідний сигнал
кожної попередньої ланки надходить на вхід наступної. Відповідно, рівняння
динаміки для групи таких ланок повинно виражати залежність вихідної величини
останньої ланки від вхідної величини першої.
Запишемо рівняння
динаміки окремих елементів. Нехай дано
n- елементів:
– для першого елемента:
Р1(р) х1вих
= Q1(p) х1вх ;
– другого елемента з врахуванням того, що:
![]()
– n-го елемента:
![]()
(8.3)
Ввівши позначення, дістанемо: P1(p) · P2(p)
· … ·Pn-1(p) = Р(р), а Q1(p) · Q2(p)
· … ·Qn-1(p) = Q(p).
Дістанемо рівняння n послідовно з’єднаних ланок у вигляді:
Рn(р) хn
вих = Q(p) х1вх (8.4)
Передаточна функція n
послідовно з’єднаних елементів матиме вигляд:
![]()
![]()
8.2. Паралельне
з'єднання ланок
У разі паралельного з'єднання ланок їхні вхідні величини
однакові, тобто вхідний сигнал для кожної ланки є ідентичним. Проте кожна ланка
має свою власну вихідну величину, яка залежить від її динаміки. Розглянемо
рівняння та передаточні функції для паралельного з'єднання ланок на прикладі
двох ланок, з’єднаних паралельно, з відповідними рівняннями динаміки:
Р1(р) х1
вих = Q1(p) х1вх ;
Р2(р) х2
вих = Q2(p) х2вх .![]()
У цьому випадку:
![]()
Звідки передаточна
функція двох паралельно з’єднаних ланок:
![]() (8.10)
(8.10)
8.3. Ланка зі зворотнім
зв’язком.
Ланка зі зворотнім зв'язком — це система, у якій частина
вихідного сигналу повертається на вхід, що дозволяє коригувати її поведінку.
Цей процес забезпечує певну регуляцію роботи системи, дозволяючи стабілізувати
чи покращити її характеристики.
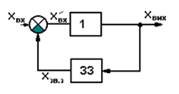
Рисунок 8.2 – Ланка зі
зворотнім зв’язком
Передаточна функція ланки, охопленої зворотним зв’язком:
![]() (8.11)
(8.11)
Поділивши чисельник і
знаменник на P1(p) Pзв(p), отримаємо:
![]() (8.12)
(8.12)
де W1(p) –
передаточна функція самої ланки без врахування зворотного зв’язку;
Wзв(р) – передаточна функція ланки
зворотного зв’язку.
Знак «–» - додатній ЗЗ. Знак «+» – від'ємний ЗЗ. Відповідно
АФХ ланки із зворотним зв’язком:
![]() (8.13)
(8.13)
8.4. Логарифмічні
частотні характеристики
Логарифмічні частотні
характеристики (ЛЧХ) використовуються для аналізу частотних властивостей
лінійних систем автоматичного керування. Вони дають змогу оцінити, як система
реагує на різні частоти вхідного сигналу, що є важливим для визначення її
стійкості, запасу стабільності та інших характеристик.
ЛЧХ зазвичай складаються з двох частин:
1. Амплітудна
характеристика (Bode amplitude plot): Вона
відображає залежність амплітуди вихідного сигналу від частоти вхідного сигналу.
Значення амплітуди вказується в децибелах (dB), що дозволяє краще оцінити
рівень посилення чи ослаблення сигналу на різних частотах.
2. Фазова
характеристика (Bode phase plot): Вона показує
зміну фази вихідного сигналу відносно вхідного в залежності від частоти. Фаза
може змінюватися в межах від -180° до +180° і надає інформацію про те, як
система змінює тимчасову структуру сигналу при його передачі через систему.
Під час побудови цих характеристик по
вертикальній осі відкладається логарифм відповідної величини, виражений у
децибелах. Щоб обчислити значення в децибелах, потрібно помножити десятковий
логарифм цієї величини на 20.
Так, АЧХ в децибелах
матиме вигляд:
L(ω) = 20lgA(ω) (8.14)
По горизонтальній осі
частоти відкладають також у логарифмічному масштабі – в октавах або декадах
(але часто записують значення самої частоти ω). Тому по горизонтальній осі
масштаб буде нерівномірним. При цьому в початку координат можна відкласти довільне
значення lgω, але не те, що відповідає ω = 0, оскільки lg0 ≈ -∞.
Одна октава є величиною, що дорівнює різниці логарифмів
деякої частоти ω і її подвоєного значення: 1 октава = lg2ω – lgω
= lg2 + lgω – lgω = lg2.
Одна декада відповідно
дорівнює різниці логарифмів: 1декада = lg10ω – lgω = 1.
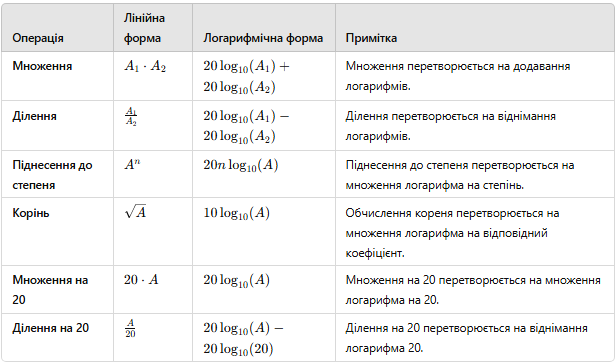
Логарифмічні характеристики є корисними для лінеаризації
частотних характеристик системи, що спрощує їх аналіз. Це дозволяє
перетворювати складні операції, такі як множення та ділення, у простіші
математичні дії, як-от додавання та віднімання, що значно полегшує побудову
характеристик для системи та її окремих елементів, приклади заміни
наведені в таблиці 8.2:
Таблиця 8.2 – Заміна
складних дій простими
Логарифмічна
амплітудно-частотна характеристика аперіодичної ланки першого порядку.
Передаточна функція цієї ланки:
![]() (8.15)
(8.15)
АФХ після позбавлення
від ірраціональності в знаменнику і виділення дійсної та уявної частини матиме
вигляд:
![]() (8.16)
(8.16)
Амплітудно-частотна характеристика має вигляд:
![]() (8.17)
(8.17)
У логарифмічних
одиницях вона запишеться так:
![]() (8.18)
(8.18)
Вираз ![]() є модулем комплексної величини 1 + jωТ, і
тому можна записати:
є модулем комплексної величини 1 + jωТ, і
тому можна записати:
20lgA(ω) = 20lgk –
20lg|1 + jTω| (8.19)
Побудуємо логарифмічну
АЧХ та ФЧХ аперіодичної ланки першого порядку (рис.8.3):
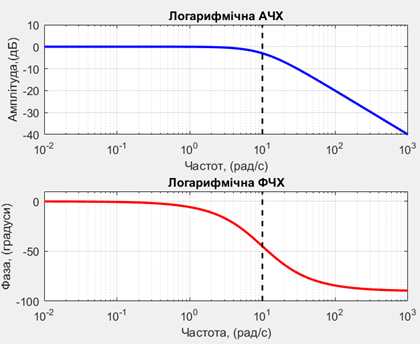
Рисунок 8.3 – ЛАЧХ аперіодичної ланки першого порядку
Побудова логарифмічних АЧХ і ФЧХ для
аперіодичної ланки першого порядку дає:
1. Частотну
селективність: Як ланка фільтрує сигнали за
частотою.
2. Фазову затримку: Як вона впливає на синхронізацію сигналу.
3. Параметри: Чітке визначення T і K
через ωc
і рівень підсилення.
4. Простоту аналізу: Логарифмічна шкала спрощує оцінку поведінки.
5. Характер відгуку: Підтвердження аперіодичної природи ланки.
Це дозволяє інженерам чи дослідникам
зрозуміти, як саме ця ланка функціонуватиме в складі більшої системи чи як
окремий елемент, і налаштувати її для конкретних задач (наприклад, фільтрація
шуму чи згладжування сигналу).
8.5. Структурні схеми та їх перетворення
Структурна схема системи автоматичного керування (САК) є
важливим етапом для візуалізації математичних моделей та функціональних
взаємозв'язків між різними елементами системи. Вона надає чітке розуміння того,
як окремі ланки системи з'єднані і як впливають одна на одну.
Основні елементи структурної схеми:
1. Ланки: У структурній схемі кожна ланка (елемент системи) зображується
прямокутником. Усередині цього прямокутника міститься інформація про динамічні
властивості ланки, що може бути представлено через передаточні функції,
рівняння динаміки або часові характеристики. Це дозволяє побачити, як система
реагує на вхідний сигнал.
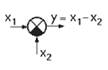
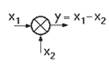
2. Підсумовування: Ланки, які здійснюють підсумовування або алгебраїчне додавання
кількох величин, зображуються колом, яке розділене на чотири рівні сектори.
Знак «мінус» або затемнення сектора вказує на різний знак вхідних величин, що
додаються. Це візуалізує процес підсумовування і дає зрозуміти, який вплив
мають різні входи на систему.
3. Зворотний зв'язок: Структурні схеми можуть також включати зворотні зв'язки, які
з'єднують виходи ланок із їх входами, коригуючи поведінку системи в реальному
часі на основі отриманих результатів.
4. Таблиця перетворень: Таблиця перетворень структурних схем служить для узагальнення
та систематизації різних типів схем, а також їх взаємодії. У таблиці можуть
бути вказані стандартні схеми, методи їх спрощення або комбінування для
побудови складніших моделей.
За допомогою структурної схеми стає можливим чітко уявити, як
працює система автоматичного керування, які елементи відповідають за різні
функції, а також зрозуміти, які зміни в системі потрібно здійснити для
оптимізації її роботи. Структурні схеми та їх перетворення наведені в таблиці
8.3
Таблиця 8.3 – Позначення структурних схем та правила
перетворення
|
№ |
Позначення
структурних схем |
|
|
1 |
Суматори |
|
|
|
|
|
|
2 |
Послідовне
з’єднання ланок |
|
|
|
||
|
3 |
Паралельне
з’єднання ланок |
|
|
|
||
|
4 |
Передаточна функція ланки із зворотним зв’язком |
|
|
е Wпр(р) = W1(р) · W2(р)
·...· Wк(р) – передаточна функція прямого каналу |
||
Продовження таблиці 8.3
|
5 |
Ланка із одиничним зворотним зв’язком |
|
|
|
||
|
|
Правила перетворення структурних схем |
|
|
6 |
1 |
2 |
|
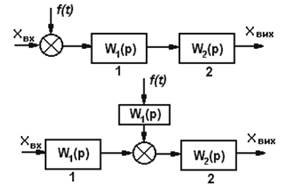
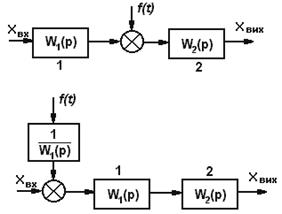
Зовнішнє збурення f(t), яке діє на вході першої ланки з
передаточною функцією W1(p) можна перенести на вхід наступної
ланки 2, додавши між збуренням і
входом ланки 2 ланку з передаточною функцією першої ланки W1(p). |
|
|
|
7 |
Зовнішнє збурення f(t), яке діє на вході ланки 2, можна
перенести на вхід попередньої послідовно виконаної ланки 1, додавши між
збуренням і входом ланки 1 ланку з передаточною функцією |
|
|
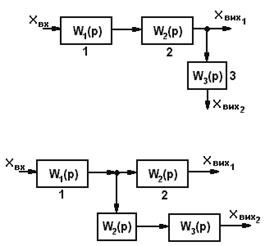
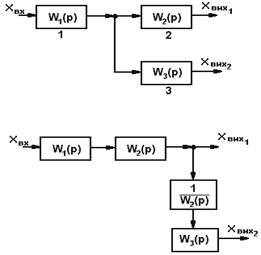
8 |
Точку з’єднання ланки 3 можна перенести із виходу ланки
2 на її вхід, додавши між виходом ланки 2 і 3 передаточну функцію ланки 2 W2. |
|
Продовження таблиці 8.3
|
9 |
1 |
2 |
|
Точку з’єднання ланки 3 можна перенести із виходу ланки
2 на її вхід, додавши між виходом ланки 2 і входом ланки 3 ланку з
передаточною функцією |
|
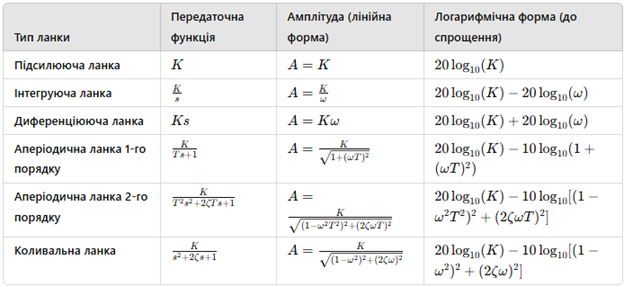
Запис
типових ланок в логарифмічному масштабі подано в таблиці 8.4:
Таблиця 8.4 – ЛАЧХ типових ланок
Питання для самоперевірки
1.
Що таке передаточна функція в системах автоматичного управління?
2.
Як можна знайти передаточну функцію системи?
3.
Що таке частотна характеристика системи?
4.
Як частотні характеристики допомагають аналізувати поведінку
системи?
5.
Чим відрізняються амплітудно-частотна характеристика (АЧХ) та
фазо-частотна характеристика (ФЧХ)?