ЛЕКЦІЯ 2.
«Кореляція, розрахунок коефіцієнтів кореляції»
Анотація
Поняття кореляція. Кореляційний момент або коваріація.
Коефіцієнт кореляції. Вибірковий кореляційний момент. Вибіркові дисперсії.
Стандартна похибка. Якісна оцінка коефіцієнтів кореляції за шкалою Чеддока. Розподіл Фішера-Іейтса.
Оцінка значимості коефіцієнта корреляції з
використанням t-критерію Стьюдента. Матриця коефіцієнтів парної кореляції.
Вибірковий коефіцієнт множинної кореляції та коефіцієнт детермінації. Вибірковий
частинний коефіцієнт кореляції. Індекс кореляції. Методика розрахунку
кореляційного відношення. Побудова економетричної
моделі на основі покрокової регресії.
1.1 Кореляція. Вибірковий
коефіцієнт кореляції
Між випадковими величинами може існувати лише стохастичний
зв'язок, при якому із зміною однієї величини змінюється розподіл іншої.
Виявлення стохастичного зв'язку та оцінка його сили – важлива і важка
задача математичної статистики. Досить сказати, що це завдання в загальному
вигляді не вирішено.
Відомо, що дисперсія суми двох незалежних величин дорівнює сумі дисперсій цих величин. Тому, якщо для двох випадкових
величин X і Y виявиться, що
D(X
+ Y) ¹ D(X) + D(Y), (2.1)
то це слугує вірною ознакою
наявності залежності між X и Y.
При виконанні вказаної нерівності будемо говорити, що випадкові
величини X і Y корельовані
і кореляція тим сильніше, чим більш
відмінні дисперсії суми від суми дисперсій.
Встановимо величину кореляції між випадковими величинами X і Y.
Безпосередньо з властивостей математичного сподівання і дисперсії випливає, що
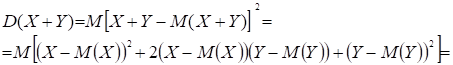 (2.2)
(2.2)
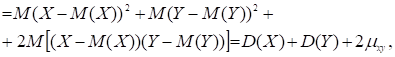
де ![]() (2.3)
(2.3)
Отже, сила кореляції визначається величиною ![]() яку з цієї причини
називають кореляційним моментом або коваріацією.
Отже, коваріація – це статистична міра взаємодії
двох змінних. Очевидно, необхідною і достатньою умовою кореляції служить
нерівність
яку з цієї причини
називають кореляційним моментом або коваріацією.
Отже, коваріація – це статистична міра взаємодії
двох змінних. Очевидно, необхідною і достатньою умовою кореляції служить
нерівність ![]() Кореляційний момент
залежить від одиниць вимірювання величин X
і Y, тому на практиці частіше
використовується безрозмірна величина
Кореляційний момент
залежить від одиниць вимірювання величин X
і Y, тому на практиці частіше
використовується безрозмірна величина
![]() (2.4)
(2.4)
яка називається коефіцієнтом кореляції.
Таким чином, якщо випадкові величини X і Y залежні, то
коефіцієнт кореляції відмінний від нуля. На жаль, зворотне твердження невірно:
з рівності ![]() не витікає
незалежність випадкових величин.
не витікає
незалежність випадкових величин.
Запишемо очевидні рівності:
![]()
![]() (2.5)
(2.5)
З визначення коефіцієнта кореляції випливає, що він не змінюється
при переході від X і Y до нормованим величин:
![]()
![]() (2.6)
(2.6)
для яких ![]() В цьому випадку з
(2.5) отримуємо
В цьому випадку з
(2.5) отримуємо
![]()
![]() (2.7)
(2.7)
звідки витікає, що ![]()
![]() тобто
тобто ![]()
Якщо коефіцієнт кореляції відмінний від нуля, то він своєю
величиною характеризує не тільки наявність, а й силу зв'язку між змінними. Чим
більше |r|, тим сильніше зв'язок (кореляція). Максимальна кореляція
значенням r=± 1. Як неважко помітити, в цьому випадку ![]() або
або ![]() , отже,
, отже, ![]() або
або ![]() Повертаючись до
величин X і Y, відмічаємо, що при r = ± 1 між ними існує строгий функціональний (причому, лінійний)
зв'язок.
Повертаючись до
величин X і Y, відмічаємо, що при r = ± 1 між ними існує строгий функціональний (причому, лінійний)
зв'язок.
Зі сказаного випливає, що при 0 < |r| <1
між Y і X може бути як стохастичний зв'язок, так і функціональний (нелінійний)
без сліду випадковості. У цьому полягає серйозний недолік коефіцієнта
кореляції. Ми можемо лише вважати, що r є показником того, наскільки зв'язок між випадковими величинами
Y і X близький до строгої лінійної залежності.
Незміщеними оцінками кореляційного моменту ![]() і дисперсій
і дисперсій
![]() і
і ![]() є вибірковий кореляційний момент (вибіркова коваріація)
є вибірковий кореляційний момент (вибіркова коваріація)
![]() і вибіркові дисперсії
і вибіркові дисперсії ![]() і
і ![]() . Тоді якщо відомі
. Тоді якщо відомі ![]() – фактичні значення змінних X і Y, то вибіркова коваріація між ними розраховується наступним чином
– фактичні значення змінних X і Y, то вибіркова коваріація між ними розраховується наступним чином
![]() , (2.8)
, (2.8)
де ![]() – середні арифметичні відповідних величин.
– середні арифметичні відповідних величин.
Видно, що у виразі для ![]() присутній один зв'язок
(добуток середніх), тому для нього, як і для вибіркових дисперсій,
число ступенів свободи дорівнює n-1.
присутній один зв'язок
(добуток середніх), тому для нього, як і для вибіркових дисперсій,
число ступенів свободи дорівнює n-1.
Той факт, що для отримання незміщеної оцінки s2 в
знаменнику вибіркової дисперсії довелося n
замінити на n-1, безпосередньо
пов'язаний з тим, що величина відносно якої беруться відхилення, сама залежить
від елементів вибірки. Якщо б у формулі вибіркової дисперсії були дві такі
величини, то n потрібно було б
замінити на n-2 і т.д.
Кожна величина, яка залежить від елементів вибірки і є у формулі
вибіркової дисперсії, називається зв'язком.
Виявляється, що знаменник вибіркової дисперсії завжди дорівнює різниці між
обсягом вибірки n і числом зв'язків, накладених на цю вибірку. Число r = n-l називається числом ступенів свободи.
Вибірковий коефіцієнт кореляції (коефіцієнт кореляції Пірсона) розраховується за формулою
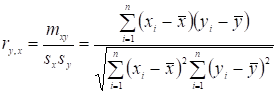 . (2.9)
. (2.9)
При цьому оцінка дисперсії характеризує ступінь розкиду значень
навколо їх середнього або варіабельність та визначається за формулою
![]() . (2.9)
. (2.9)
В загальному випадку для отримання незміщеної оцінки дисперсії
суму квадратів необхідно поділити на число ступенів свободи. Так як вибірка вже
використовувалася один раз для визначення середнього Х, то число накладених зв’язків в даному випадку дорівнює одиниці, а число
ступенів свободи ![]() .
.
Однак, більш природно вимірювати ступінь розкиду значень змінних
в тих же одиницях, в яких вимірюється і сама змінна. Цю задачу вирішує
показник, що називається середньоквадратичним
відхиленням (стандартним відхиленням)
або стандартною похибкою і
визначається співвідношенням
![]() . (2.9)
. (2.9)
Для якісної оцінки коефіцієнтів кореляції застосовуються різні
шкали, найбільш часто – шкала Чеддока. В
залежності від значень коефіцієнта кореляції зв'язок може мати одну з оцінок
0,1-0,3 – слабкий;
0,3-0,5 – помітний;
0,5-0,7 – помірний;
0,7-0,9 – високий;
0,9-1,0 – вельми високий.
Варто відмітити, що величина коефіцієнта кореляції не є доказом
того, що між ознаками, що досліджуються, є причинно-наслідковий зв'язок, а
являє собою оцінку ступеня взаємної узгодженості в змінах ознак. Для того, щоб
встановити причинно-наслідкову залежність необхідним є аналіз якісної природи
явищ.
Так як оцінка тісноти зв’язку за допомогою коефіцієнта кореляції
проводиться, як правило, на основі більш чи менш обмеженої інформації про
явище, що досліджується, то виникає питання: наскільки правомірним є висновок
по вибірковим даним про наявність кореляційного зв’язку в тій генеральній
сукупності. з якої була отримана вибірка?
Нехай X і Y мають нормальний розподіл. У цьому
випадку при досить великому обсязі вибірки n
коефіцієнт r наближено дорівнює
генеральному коефіцієнту r. Проте оцінити похибку, яка виникає при цьому, дуже важко.
Це і не обов’язково, оскільки точне
значення r в розрахунках практично не
використовується, а треба лише як показник наявності кореляції між Y і X.
Вибірковий коефіцієнт кореляції r
застосовується в основному для перевірки загальної гіпотези про наявність
кореляції між спостережуваними величинами, не вдаючись у детальні оцінки сили
цієї кореляції.
У зв'язку з випадковістю вибірки r може бути відмінно від нуля, навіть якщо між спостережуваними величинами
немає кореляції. Отже, для перевірки гіпотези про відсутність кореляції,
необхідно перевіряти, значимо чи r відрізняється від нуля. А для цього потрібно
знати розподіл r як випадкової
величини. Цей розподіл відомий, але, як і варто було очікувати, воно залежить
від невідомого генерального коефіцієнта r. Однак, якщо ми як нульову візьмемо гіпотезу, що r= 0 (відсутність кореляції), то r-розподіл відповідний r= 0, сильно спрощується і буде залежати тільки від обсягу
вибірки. Його щільність має вигляд
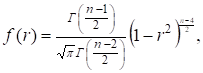
![]() (2.10)
(2.10)
r-Розподіл називають розподілом Фішера-Іейтса.
Видно, що це симетричний відносно нуля унімодальний
розподіл. У статистичних таблицях наведені квантилі
цього розподілу для деяких рівнів значимості та ступенів свободи.
У припущенні, що
генеральна кореляція r= 0, інтервальна оцінка для r з довірчою ймовірністю р = 1 - a,
очевидно, дорівнює
![]() .
.
Отже, якщо виявиться, що знайдений за вибіркою коефіцієнт r
задовольняє нерівності
![]() (2.11)
(2.11)
то його потрібно визнати
значущим, тобто потрібно вважати, що нульова гіпотеза невірна. А це означає, що
r ¹ 0 і між величинами, що
спостерігаються, є кореляція. Вона буде тим сильніше, чим значніше | r |
перевищує ![]() і наближається до 1.
і наближається до 1.
Оцінка значимості коефіцієнта корреляції
при малих обсягах вибірки виконується з використанням t-критерію Стьюдента. При
цьому фактичне (спостережне) значення цього критерію визначається за формулою
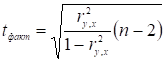 . (2.12)
. (2.12)
Розраховане за цією формулою значення порівнюється з критичним
значенням t-критерію Стьюдента з урахуванням заданного
рівня значущості ![]() та числа ступенів
свободи n-2.
та числа ступенів
свободи n-2.
Якщо ![]() , то отримане значення коефіцієнта кореляції признається
значущим і робиться висновок про тісний статистичний взаємозв’язок величин.
, то отримане значення коефіцієнта кореляції признається
значущим і робиться висновок про тісний статистичний взаємозв’язок величин.
В MS Excel для розрахунку
кореляції можна використовувати функцію КОРРЕЛ(), а для знаходження критичного
значення t-статистики Стьюдента СТЬЮДРАСПРОБР().
1.2 Матриця коефіцієнтів
парної кореляції
Коефіцієнти парної кореляції використовуються для виміру сили
лінійних зв’язків різних пар ознак з їх множини. Для
множини ознак отримують матрицю
коефіцієнтів парної кореляції.
Нехай вся сукупність даних складається зі змінної ![]() та m змінних (факторів) Х, кожна з яких містить n спостережень. Тоді можна розрахувати
матрицю коефіцієнтів парної кореляції R,
вона симетрична відносно гловної діагоналі
та m змінних (факторів) Х, кожна з яких містить n спостережень. Тоді можна розрахувати
матрицю коефіцієнтів парної кореляції R,
вона симетрична відносно гловної діагоналі
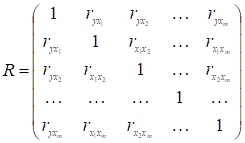 . (2.13)
. (2.13)
Аналіз матриці коефіцієнтів парної кореляції використовується при
побудові моделей множинної регресії.
Однією кореляційною матрицею неможливо повністю описати залежності
між величинами. У зв’язку з цим в багатомірному кореляційному аналізі
розглядаються дві задачі:
1) визначення тісноти
зв’язку однієї випадкової величини з сукупністю інших величин, що включені в
дослідження;
2) визначення тісноти
зв’язку між двома величинами при фіксуванні або виключенні впливу інших
величин.
Ці задачі вирішуються відповідно за допомогою множинної чи
частинної кореляції.
1.3 Коефіцієнти множинної
та частинної кореляції
Вибірковий коефіцієнт множинної кореляції визначається за формулою
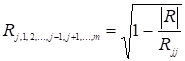 , (2.14)
, (2.14)
де ![]() – визначник кореляційної матриці
– визначник кореляційної матриці ![]() ;
;
![]() – алгебраїчне
доповнення елемента
– алгебраїчне
доповнення елемента ![]() тієї ж матриці.
тієї ж матриці.
Квадрат коефіцієнта множинної кореляції ![]() прийнято називати вибірковим множинним коефіцієнтом
детермінації. Він показує яку частку варіації (випадкового розкиду) досліджуємої величини
прийнято називати вибірковим множинним коефіцієнтом
детермінації. Він показує яку частку варіації (випадкового розкиду) досліджуємої величини ![]() пояснює варіація інших
випадкових величин
пояснює варіація інших
випадкових величин ![]() .
.
Перевірка значущості коефіцієнта детермінації здійснюється
шляхом порівняння розрахункового значення F-критерію Фішера
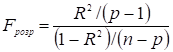 , (2.15)
, (2.15)
з табличним ![]() . Табличне значення критерію визначається заданим рівнем
значущості
. Табличне значення критерію визначається заданим рівнем
значущості ![]() та числа ступенями свободи
та числа ступенями свободи
![]() та
та ![]() (де p – кількість
параметрів моделі). Коефіцієнт
(де p – кількість
параметрів моделі). Коефіцієнт ![]() значимо відрізняється
від нуля, якщо виконується нерівність
значимо відрізняється
від нуля, якщо виконується нерівність
![]() .
.
Якщо випадкові величини, що розглядаються, корелюють один з одним,
то на величину парної кореляції частково мають вплив інші величини. У зв’язку з
цим виникає необхідність дослідження частинної кореляції між величинами при
виключенні впливу інших випадкових величин (однієї чи декількох).
Вибірковий частинний коефіцієнт кореляції визначається за формулою
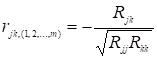 , (2.16)
, (2.16)
де ![]() – алгебраїчні доповнення до відповідних елементів
матриці
– алгебраїчні доповнення до відповідних елементів
матриці ![]() .
.
За умови, що m=3, вираз (2.16) буде мати вигляд
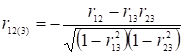 , (2.17)
, (2.17)
Коефіцієнт ![]() називається
коефіцієнтом кореляції між
називається
коефіцієнтом кореляції між ![]() та
та ![]() при фіксованому
при фіксованому ![]() .
.
1.4 Оцінка тісноти
нелінійного зв’язку
При відхиленні парної статистичної залежності від лінійної
коефіцієнт кореляції втрачає свій сенс як характеристика тісноти зв’язку. В
такому випадку можна використати такий вимірник зв’язку як індекс кореляції (кореляційне
відношення). Кореляційне відношення визначається через відношення між
групової дисперсії до загальної дисперсії.
Для визначення емпіричного кореляційного відношення сукупність
значень результативної ознаки Y розбивають на окремі групи. В основу групування
кладеться фактор Х, що досліджується.
Коли сукупність, що досліджується, розбивається на групи по одній
(факторній) ознаці Х, то для кожної з цих груп можна розрахувати відповідні
групові середні результативної ознаки. Зміна групових середніх від групи до
групи говорить про наявність зв’язку результативної ознаки з факторною однакою,
а наближена рівність групових середніх – про відсутність зв’язку.
Методика розрахунку кореляційного відношення.
Нехай групування даних зроблено, при цьому k – число інтервалів групування по вісі
х; ![]() – кількість елементів вибірки в j-тому інтервалі
групування; n – обсяг сукупності
(
– кількість елементів вибірки в j-тому інтервалі
групування; n – обсяг сукупності
(![]() );
);![]() – загальне середнє.
– загальне середнє.
1. Розрахуємо середнє значення Y в j-й групі:
![]() . (2.18)
. (2.18)
2. Розрахуємо загальну середню Y, використовуючи середні значення
в кожній групі:
![]() . (2.19)
. (2.19)
3. Знайдемо міжгрупову дисперсію та
загальну дисперсію
![]() ;
; ![]() . (2.20)
. (2.20)
Кореляційне відношення ![]() залежної змінної Y по
незалежній змінній Х може бути отримано з відношення між групової дисперсії до
загальної дисперсії
залежної змінної Y по
незалежній змінній Х може бути отримано з відношення між групової дисперсії до
загальної дисперсії
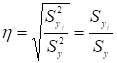 . (2.21)
. (2.21)
Величина кореляційного відношення змінюється від 0 до 1.
Близькість його до нуля говорить про відсутність зв’язку, а близькість до
одиниці – про тісний зв'язок.
1.5 Побудова економетричної моделі на основі покрокової регресії
Оцінювання параметрів економетричної
моделі та її дисперсійний аналіз становлять загальний процес побудови моделі.
Поєднання цих частин зумовило появу методу оцінювання параметрів моделі 1МНК,
яка базується на елементах дисперсійного аналізу.
При елементарному тлумаченні взаємозв’язку між двома змінними за
допомогою 1МНК увагу, як правило, акцентують на коефіцієнтах кореляції. Причому
неважко показати, що
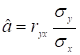 , (2.22)
, (2.22)
де ryx –
парний коефіцієнт кореляції між Y та X; ![]() – середньоквадратичне відхилення залежної змінної;
– середньоквадратичне відхилення залежної змінної; ![]() – середньоквадратичне відхилення незалежної змінної.
– середньоквадратичне відхилення незалежної змінної.
Отже,оцінка параметрів моделі прямо
пропорційна до коефіцієнта парної кореляції. Аналогічні співвідношення
виконуються і в загальному випадку.
А це означає, що оцінити параметри моделі можна через коефіцієнти
кореляції: спочатку оцінити тісноту зв’язку між кожною парою змінних, а потім
знайти оцінки параметрів економетричної моделі.
Залежність оцінок параметрів економетричної
моделі і коефіцієнтів парної кореляції покладено в основу алгоритму покрокової
регресії.
Опишемо цей алгоритм.
Крок 1-й. Усі вихідні дані змінних
стандартизуються (нормалізуються):
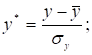
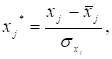 (2.23)
(2.23)
де ![]() – нормалізована залежна змінна;
– нормалізована залежна змінна; ![]() – нормалізовані незалежні змінні;
– нормалізовані незалежні змінні; ![]() – середнє значення j-ї
незалежної змінної;
– середнє значення j-ї
незалежної змінної; ![]() – середнє значення залежної змінної;
– середнє значення залежної змінної; ![]() ,
, ![]() – середньоквадратичні відхилення.
– середньоквадратичні відхилення.
При цьому середні значення ![]() і
і ![]() дорівнюють нулю, а
дисперсії – одиниці.
дорівнюють нулю, а
дисперсії – одиниці.
Крок 2-й. Знаходиться кореляційна
матриця (матриця парних коефіцієнтів кореляції):
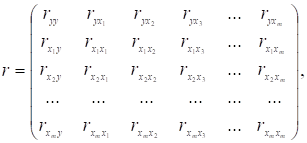 (2.24)
(2.24)
де ![]() – парні коефіцієнти кореляції між залежною і
незалежними змінними,
– парні коефіцієнти кореляції між залежною і
незалежними змінними,
![]()
n – кількість спостережень;
![]() – парні коефіцієнти кореляції між незалежними змінними,
– парні коефіцієнти кореляції між незалежними змінними,
![]()
Крок 3-й. На підставі порівняння абсолютних
значень ![]() вибираються
вибираються ![]() Найбільше
Найбільше ![]() вказує на ту незалежну
змінну, яка найтісніше пов’язана з y.
На цьому кроці на основі 1МНК знаходиться оцінка параметра цієї змінної в
моделі:
вказує на ту незалежну
змінну, яка найтісніше пов’язана з y.
На цьому кроці на основі 1МНК знаходиться оцінка параметра цієї змінної в
моделі:
![]() , (2.25)
, (2.25)
де ![]() – оцінка параметру моделі, яка будується на основі
стандартизованих даних.
– оцінка параметру моделі, яка будується на основі
стандартизованих даних.
Крок 4-й. Серед інших значень ![]() вибирається
вибирається ![]() і в модель вводиться наступна
незалежна змінна
і в модель вводиться наступна
незалежна змінна
![]() (2.26)
(2.26)
і т.д.
Якщо немає обмеження на внесення до економетричної
моделі кожної наступної незалежної змінної, то обчислення виконуються доти,
поки поступово не будуть внесені до моделі всі змінні.
Сума квадратів залишків для такої моделі запишеться так:
![]() .
.
звідси мінімізації підлягає
![]() .
.
Узявши похідну за кожним невідомим параметром bj цієї функції і прирівнявши всі
здобуті похідні нулю, дістанемо систему нормальних рівнянь.
Система нормальних рівнянь для знаходження параметрів моделі bj в загальному вигляді запишеться так:
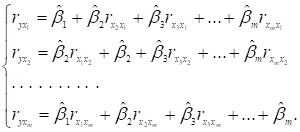
Позначимо матрицю парних коефіцієнтів кореляції між незалежними
змінними через r, а вектор парних
коефіцієнтів кореляції між залежною і незалежними змінними через ![]() . тоді система нормальних рівнянь набере вигляду
. тоді система нормальних рівнянь набере вигляду
![]() ,
,
а оператор оцінювання
параметрів:
![]() (2.27)
(2.27)
Оскільки всі змінні виражені в стандартизованому масштабі, то
параметри ![]() показують порівняльну
силу впливу кожної незалежної змінної на залежну: чим більше за модулем
значення параметра
показують порівняльну
силу впливу кожної незалежної змінної на залежну: чим більше за модулем
значення параметра ![]() , тим сильніше впливає j-та
змінна на результат.
, тим сильніше впливає j-та
змінна на результат.
Зв’язок між оцінками параметрів моделі на основі стандартизованих
і нестандартизованих змінних запишеться так:
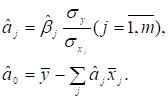 (2.28)
(2.28)
Приклад 2.1. Для десяти цехів машинобудівного підприємства наведено такі дані
(табл. 2.1).
Побудуємо економетричну модель, яка
описуватиме зв’язок продуктивності праці з наведеними чинниками згідно з
алгоритмом покрокової регресії.
Таблиця 2.1
|
Номер цеху |
Середньомісячна
зарплата у |
Продуктивність
праці х1 |
Фондомісткість
продукції х2 |
виконання норми
виробітку х3, % |
|
1 |
45 |
265 |
0,20 |
130 |
|
2 |
42 |
236 |
0,04 |
127 |
|
3 |
50 |
257 |
0,30 |
151 |
|
4 |
55 |
279 |
0,20 |
149 |
|
5 |
40 |
226 |
0,10 |
140 |
|
6 |
70 |
350 |
0,10 |
141 |
|
7 |
56 |
278 |
0,25 |
152 |
|
8 |
57 |
262 |
0,03 |
188 |
|
9 |
55 |
269 |
0,15 |
120 |
|
10 |
53 |
250 |
0,32 |
126 |
Запишемо кореляційну матрицю для цих
вихідних даних:
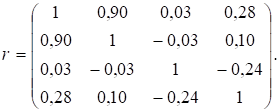
Із матриці бачимо, що діагональні її елементи дорівнюють одиниці,
бо вони характеризують зв’язок кожної змінної із собою. Ця матриця квадратна і
симетрична.
У першому рядку містяться коефіцієнти парної кореляції, що
характеризують тісноту зв’язку кожної змінної з продуктивністю праці.
Так,
![]() = 0,9;
= 0,9; ![]() = 0,03;
= 0,03; ![]() = 0,28.
= 0,28.
де ![]() – продуктивність праці;
– продуктивність праці; ![]() – зарплата;
– зарплата; ![]() – фондомісткість продукції;
– фондомісткість продукції; ![]() – % виконання норми виробітку.
– % виконання норми виробітку.
Оскільки серед величин максимальне значення ![]() = 0,9, то спочатку
будуватиметься модель:
= 0,9, то спочатку
будуватиметься модель: ![]() Порівнявши потім інші
два коефіцієнти:
Порівнявши потім інші
два коефіцієнти:
max{![]() = 0,03;
= 0,03; ![]() = 0,28} = 0,28, введемо до моделі змінну
= 0,28} = 0,28, введемо до моделі змінну ![]() :
:
![]()
і, нарешті,
![]()
Далі, використовуючи співвідношення (2.28), обчислимо оцінки
параметрів моделі для вихідної нестандартизованої інформації.
У результаті дістанемо такі регресійні рівняння зв’язку:
1) ![]() ;
;
2) ![]()
3) ![]()