ЛЕКЦІЯ 1. «Загальні поняття фінансових економетричних моделей»

Анотація

Термін «економетрія». Задачі економетрії. Просторові дані. Часові ряди. Особливості часових рядів. Кореляційно-регресійний аналіз в економіці. Функціональний та кореляційний зв’язки. Функція регресії. Регресор. Регресат. Причини обов'язкової присутності в регресійних моделях випадкового фактора. Кореляційне поле. Економетрична модель. Специфікація моделі регресії. Параметризація рівняння регресії. Моделі часових рядів. Регресійні моделі з одним рівнянням. Системи незалежних, рекурсивних, взаємозалежних рівнянь. Порівнянність та однорідність даних. Повнота даних та стійкість.

1.1 Основні поняття економетрії

Термін «економетрика» з’явився в літературі на початку ХХ століття і означав «економетричні виміри». Термін «економетрика» (економетрія) був введений в словесний обіг ще в 1910 р. П. Чомпою в книзі «Нарис економетрії і природничої бухгалтерії, основаної на політичній економії», яка була надрукована у м.Львові. В подальшому цьому термінові значну увагу приділяв норвезький вчений Р.Фріш (1895-1973), який наголосив, що економетрія є синтезом економічної теорії, математики і статистики. Офіційною датою народження нового напрямку економічних досліджень вважають 29 грудня 1930р., коли за ініціативою Р. Фріша було створено «Міжнародне товариство розвитку економічної теорії в її зв’язку зі статистикою і математикою». В 1933р. це товариство почало видавати журнал «Економетрика».

На сьогоднішній день відсутнє єдине загальноприйняте визначення економетрики. Наведемо деякі з них.

Економетрія (економетрика) – наука, що вивчає конкретні кількісні взаємозв’язки економічних об’єктів та процесів за допомогою математичних та статистичних методів та моделей (Большой энциклопедический словарь, 1997).

Економетрика (Econometrics) – сукупність методів аналізу зв’язків між різними економічними показниками (факторами) на основі реальних статистичних даних з використанням апарату теорії ймовірності та математичної статистики. за допомогою цих методів можна виявити нові, не відомі раніше зв’язки, уточнити чи спростувати гіпотези про існування визначених зв’язків між економічними показниками, що пропонуються економічною теорією (Носко В.П.).

Економетрика – це самостійна наукова дисципліна, що об’єднує сукупність теоретичних результатів, прийомів, методів та моделей, призначена для того, щоб на базі економічної теорії, економічної статистики, математико-статистичного інструментарію надавати конкретний кількісний вираз загальним закономірностям, що обумовлені економічною теорією взаємозв’язків економічних явищ та процесів (С.А. Айвазян).

Свідоцтвом того, що економетрика займає пристойне місце, є присудження за найбільш видатні розробки в цій сфері Нобелівських премій з економіки Рагнару Фрішу і Яну Тінбергену (1969), Лоуренсу Клейну (1980), Трюгве Хаавельмо (1989), Роберту Лукасу (1995), Джеймсу Хекману і Даніелю Мак-Фаддену (2000), Роберту Ф. Енглу і Клайву У. Дж. Грейнджеру (2003).

В економетричних дослідженнях використовують наступні типи економічних даних:

просторові – характеризують ситуацію з конкретної змінної (чи набору змінних), що відносяться до просторово розділеним схожим об’єктам в один і той же момент часу. Наприклад, дані по курсу купівлі та продажу валюти в конкретний день в різних обмінних пунктах міста;

часові ряди – відображають зміни (динаміку) якої-небудь змінної на проміжку часу. Наприклад, щоквартальні дані по інфляції, національному доходу за декілька років.

В економетриці вирішуються задачі опису даних, перевірки гіпотез, відновлення залежностей, класифікація об’єктів та ознак, прогнозування, прийняття статистичних рішень тощо.

При виборі методу аналізу конкретних економічних даних слід враховувати, що вони мають ряд особливостей.

Специфіка економічних даних:

1. Багато економічних показників невід’ємні. Значить їх потрібно описувати невід’ємними випадковими величинами.

2. Частка нечислових даних в економіці істотно вище ніж в техніці. Отже, частіше застосовується статистика об’єктів нечислової природи.

3. Кількість об’єктів, що вивчаються, в економічному дослідженні часто обмежена, тому обґрунтування ймовірнісних моделей в ряді випадків ускладнено.

4. Економічні процеси розвиваються в часі, тому велике місце в економетриці займають питання аналізу та прогнозування часових рядів, в тому числі багатомірних. При цьому слід відмітити, що часові ряди якісно відрізняються від простих статистичних вибірок.

Особливості часових рядів:

а) послідовні в часі рівні часових рядів є взаємозалежними, особливо це відноситься до близько розташованих спостережень;

б) в залежності від моменту спостереження рівні в часових рядах мають різну інформативність: інформаційна цінність спостережень спадає в міру їх віддалення від поточного моменту часу;

в) зі збільшенням кількостей рівнів часового ряду точність статистичних характеристик не збільшується пропорційно числу спостережень, а при появі нових закономірностей може навіть зменшуватися.

1.2 Кореляційно-регресійний аналіз в економіці

Економічні дані представляють собою кількісні характеристики яких-небудь економічних об’єктів чи процесів. Вони формуються під дією безлічі факторів. не всі з яких доступні зовнішньому контролю. Фактори, що не контролюються можуть приймати випадкові значення з деякої множини значень і тим самим обумовлювати випадковість даних, які вони визначають. Стохастична (ймовірнісна) природа економічних даних обумовлює необхідність застосування відповідних статистичних методів для їх обробки та аналізу.

Дослідження показують,що варіація кожної ознаки знаходиться в тісному зв’язку і взаємодії з варіацією інших ознак, що характеризують сукупність одиниць,які досліджуються. Розглядаючи залежності між ознаками, необхідно виділити два типи зв’язку:

-                функціональні – характеризуються повною відповідністю між зміною факторної ознаки та зміною результативного показника: кожному значенню фактора відповідають визначені значення результативної ознаки. Цей тип зв’язку виражається у вигляді формульної залежності;

-                кореляційні – між змінами двох ознак не має повної відповідності, вплив окремих факторів виявляється лише у середньому, при масовому спостереженні фактичних даних. Одночасний вплив на однаку, що вивчається, великої кількості різних факторів призводить до того, що одному і тому ж значенню ознаки-фактора відповідає цілий розподіл значень результативної ознаки, оскільки в кожному конкретному випадку інші факторні ознаки можуть змінювати силу і направленість своєї дії.

Отже, при наявності кореляційної залежності встановлюється лише тенденція зміни результативної ознаки при зміні величини факторної ознаки.

Вивчаючи взаємозв’язок між ознаками їх класифікують

-                по направленості: прямі та обернені;

-                по формі: лінійні та нелінійні;

-                за кількістю факторів: однофакторні та багатофакторні.

Варто мати на увалі, що статистичний аналіз залежностей сам по собі не розкриває сутності причинних зв'язків між явищами, тобто він не вирішує питання, з яких причин одна змінна впливає на іншу. Розв'язок такої задачі є результатом якісного (змістовного) вивчення зв'язків, що обов'язково має або передувати статистичному аналізу, або супроводжувати його.

Нехай з певних економічних міркувань встановлено, що деякий економічний показник є причиною змінювання іншого показника . Статистичні дані по кожному з показників інтерпретуються як деякі реалізації випадкових величин X і Y. Як відомо з курсу теорії ймовірностей, математичним сподіванням випадкової величини називається її середнє (арифметичне чи зважене) значення. А залежність середнього значення від іншої випадкової величини зображується за допомогою умовного математичного сподівання.

Кореляційну залежність між ними або залежність в середньому в загальному випадку можна подати у вигляді співвідношення

(1.1)

де  – умовне математичне сподівання.

Функція називається функцією регресії Y на X. При цьому X називається незалежною (пояснюючою, екзогенною) змінною (регресором) або факторною ознакою, Y залежною (пояснюваною, ендогенною) змінною (регресатом) або результативною ознакою. Розглядаючи залежність двох випадкових величин, говорять про парну регресію.

Залежність Y від кількох змінних, що описується функцією

(1.2)

називають множинною регресією.

Однак реальні значення залежної змінної не завжди збігаються з її умовним математичним сподіванням, тому аналітична залежність (у вигляді функції ) має бути доповнена випадковою складовою , що, власне, і вказує на стохастичну сутність залежності.

Означення 1.1. Зв'язки між залежною та незалежною (незалежними) змінними, що описуються співвідношеннями

(1.3)

(1.4)

називають регресійними рівняннями (моделями).

Виникає питання про причини обов'язкової присутності в регресійних моделях випадкового фактора (відхилення). Серед таких причин виокремимо найістотніші.

1. Уведення в модель не всіх пояснюючих змінних. Будь-яка регресійна (зокрема, економетрична) модель – це спрощення реальної ситуації. Остання завжди є складною композицією різних факторів, багато з яких у моделі не враховуються, що призводить до відхилення реальних значень залежної змінної від її модельних значень.

Наприклад, попит на товар визначається його ціною, цінами на товари-замінники, на товари, що його доповнюють, прибутком споживачів, їхніми смаками, уподобаннями тощо. Безумовно, перелічити всі пояснюючі змінні практично неможливо. Зокрема, неможливо врахувати такі фактори, як традиції, національні чи релігійні особливості, географічне положення району, погоду та багато інших, вплив яких призводить до деяких відхилень реальних спостережень від модельних. Ці відхилення можуть бути описані як випадкова складова моделі.

У деяких випадках заздалегідь невідомо, які фактори за умов, що склалися, насправді є визначальними, а якими можна знехтувати. Крім того, інколи безпосередньо врахувати якийсь фактор неможливо через відсутність статистичних даних. Наприклад, обсяг заощаджень домогосподарств може визначатися не лише прибутками їх членів, а й станом здоров'я останніх, інформація про яке в цивілізованих країнах становить лікарську таємницю. У деяких ситуаціях ряд факторів має принципово випадковий характер, що додає неоднозначності певним моделям, наприклад погода в моделях, що прогнозують обсяг врожаю.

2. Неправильний вибір функціональної форми моделі через слабку вивченість досліджуваного процесу або через його мінливість може бути неправильно дібрано функцію, що його моделює. Це, безумовно, спричинить відхилення моделі від реальності, що позначиться на величині випадкової складової. Наприклад виробнича функція (Y) одного фактора (X) може моделюватися функцією , хоча мала б використовуватися інша модель: , що враховує закон спадної ефективності. Крім топ), неправильним може бути добір пояснюючих змінних.

3. Агрегування змінних. У багатьох моделях розглядаються залежності між факторами, що самі є складною комбінацією інших, простіших змінних. Наприклад, при вивченні сукупного попиту аналізується залежність, у якій пояснювана змінна (сукупний попит) є складною композицією індивідуальних попитів, що також може виявитися причиною відхилення реальних значень від модельних.

4. Помилки вимірювань. Якою б якісною не була модель, помилки вимірювання змінних впливатимуть на розбіжності між модельними та емпіричними даними, що також позначиться на величині випадкового члена.

5. Обмеженість статистичних даних. Найчастіше будуються моделі, що описуються неперервними функціями. А для оцінювання параметрів моделі використовується набір даних, що має дискретну структуру. Ця невідповідність знаходить відображення у випадковому відхиленні.

6. Непередбачуваність людського фактора. Ця причина може "зіпсувати" найякіснішу модель. Дійсно, при правильному виборі форми моделі, скрупульозному доборі пояснюючих змінних неможливо спрогнозувати поведінку кожного індивідуума.

Сукупність методів, за допомогою яких досліджуються та узагальнюються взаємозв'язки кореляційно пов'язаних змінних, називається кореляційно-регресійним аналізом.

Зазначеними методами розв'язують дві основні задачі:

1) знаходження загальної закономірності, що характеризує залежність двох (чи більше) кореляційно пов'язаних змінних, тобто розробка математичної моделі зв'язку (задача регресійного аналізу);

2) визначення тісноти зв'язку (задача кореляційного аналізу).

Здебільшого процедура аналізу зв'язку між змінними дає змогу встановити його природу, тобто визначити форму залежності між змінними.

Побудова якісного рівняння регресії, що відповідає емпіричним даним і цілям досліджень, є досить складним процесом. Його можна поділити на три етапи:

1) вибір форми рівняння регресії;

2) визначення параметрів обраного рівняння;

3) аналіз якості рівняння та перевірка адекватності рівняння емпіричним даним, удосконалення рівняння.

Вибір форми зв'язку змінних називається специфікацією моделі регресії.

У випадку парної регресії вибір формули звичайно здійснюється за графічним зображенням реальних статистичних даних у вигляді точок у декартовій системі координат, що називається кореляційним полем (діаграмою розсіювання) (рис. 1.1).

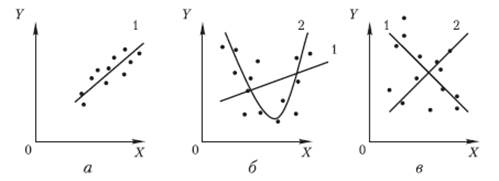
Рисунок 1.1 – Вибір регресії за графічним зображенням реальних даних

На рис. 1.1 проілюстровано три ситуації.

На графіку 1.1, а взаємозв'язок між X і Y близький до лінійного, і пряма 1 досить добре узгоджується з емпіричними точками. Тому щоб описати залежність між X і Y, доцільно вибрати лінійну функцію . На графіку 1.1, б реальний взаємозв'язок між X і Y, найімовірніше, описується квадратичною функцією (лінія 2). На графіку 1.1, в явний взаємозв'язок між X і Y відсутній. Тому, щоб краще вибрати форму зв'язку, необхідно, можливо, збільшити кількість спостережень – точок кореляційного поля або скористатися іншими способами вимірювання показників. Часто для визначення форми залежності використовують спеціальні методи, наприклад, метод характерних середніх (СР.02).

У випадку множинної регресії визначити форми залежності ще складніше.

Якщо природа зв'язку невідома, то співвідношення між показниками описують за допомогою наближених спрощених форм залежностей, насамперед лінійних.

Однак поки не обчислено кількісні значення коефіцієнтів й не перевірено надійність отриманих результатів, зазначена формула залишається лише гіпотезою.

1.3 Економетрична модель та її елементи

Економетрична модель – це логічний (звичайно математичний) опис того, що економічна теорія вважає особливо важливим при дослідженні певної проблеми.

Як правило, модель має форму рівняння чи системи рівнянь, що характеризують виокремлені дослідником взаємозалежності між економічними показниками. Економетрична модель, що пояснює поведінку одного показника, складається з одного рівняння, а модель, що характеризує зміну кількох показників, – із такої самої кількості рівнянь. У моделі можуть бути також тотожності, що відбивають функціональні зв'язки в певній економічній системі. Оскільки така модель поєднує не лише теоретичний, якісний аналіз взаємозв'язків, а й емпіричну інформацію, то в ній, на відміну від просто економічної моделі, завжди присутні стохастичні залишки. Саме ймовірнісні характеристики залишків моделі зумовлюють якість тієї чи іншої аналітичної форми моделі.

Отже, сформулюємо таке означення економетричної моделі.

Означення 1.2. Економетрична модель – це функція чи система функцій, що описує кореляційно-регресійиий зв'язок між економічними показниками, причому залежно від причинних зв'язків між ними один чи кілька із цих показників розглядаються як залежні змінні, а інші – як незалежні.

У загальному випадку рівняння в економетричній моделі має вигляд

(1.5)

де Y – результат, або залежна змінна, змінювання якої описує дане рівняння;  – фактори, або незалежні змінні, що визначають поведінку Y. Змінна містить ту частину руху Y, що не пояснюється змінними , і має випадковий характер. Символ F відображує аналітичний вид зв'язку між досліджуваними змінними.

Означення 1.3. Процес опису явища чи процесу, тобто вибір аналітичної форми моделі, називається специфікацією моделі. Іншими словами, специфікація моделі – це аналітична форма залежності між економічними показниками.

Функція F у кожному конкретному випадку окрім змінних і містить ще щонайменше деякі коефіцієнти, що поєднують змінні у певних співвідношеннях і визначають структуру рівняння. Ці коефіцієнти називаються параметрами моделі.

Означення 1.4. Визначення значень коефіцієнтів (параметрів) обраної форми статистичного зв'язку змінних на підставі відповідних статистичних даних називається параметризацією рівняння регресії або оцінюванням параметрів.

Ці рівняння, а отже, і параметри визначають структуру моделі: вони вказують на характер припустимих співвідношень між змінними.

Можна виділити три основні класи економетричних моделей, які застосовуються для аналізу та прогнозування економічних систем:

1) моделі часових рядів;

2) регресійні моделі з одним рівнянням;

3) системи економетричних рівнянь.

Моделі часових рядів являють собою моделі залежності результативної ознаки від часу:

. (1.6)

В регресійних моделях з одним рівнянням залежна змінна Y може бути представлена у вигляді функції (1.5). В залежності від виду функції моделі поділяються на лінійні та нелінійні, а в залежності від включених в модель факторів – на однофакторні та багатофакторні.

Приклади задач, що розв’язуються за допомогою регресійних моделей:

-                дослідження залежності заробітної плати Y від віку , рівня освіти , статі , стажу роботи :

;

-                прогноз та планування випуску продукції за факторами виробництва (виробнича функція Кобба-Дугласа означає, що обсяг випуску продукції Y є функції кількості капіталу K та кількості праці L)

.

Системи економетричних рівнянь застосовують у тому випадку, коли економічні явища настільки складні, що неможливо описати їх за допомогою тільки одного рівняння. Моделі з одним рівнянням не відображають взаємозв’язок між пояснюючими змінними чи їх зв'язок з іншими змінними. До того ж деякі змінні можуть здійснювати взаємні впливи і важко визначити, яка з них є залежною, а яка незалежною. Тому при побудові економетричних моделей застосовують системи рівнянь.

Виділяють наступні три види економетричних систем:

1) системи незалежних рівнянь;

2) системи рекурсивних рівнянь;

3) системи взаємозалежних рівнянь.

В системах незалежних рівнянь кожна залежна змінна представлена як функція одного й того ж набору незалежних змінних :

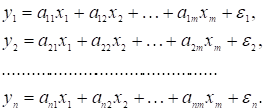. (1.7)

Кожне рівняння даної системи можна розглядати як самостійно як рівняння регресії.

В системах рекурсивних рівнянь залежні змінні представлені як функції незалежних змінних та визначених раніше залежних змінних :

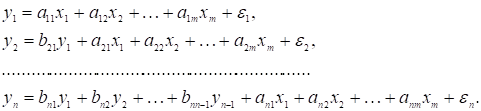(1.8)

Розглянемо, наприклад, систему з трьох рівнянь

.

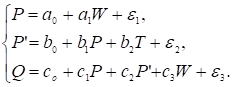де P – ціна на бавовну, P’ – ціна бавовняні вироби, Q – кількість проданих бавовняних виробів, W – індекс погодних умов, T – податкові тарифи на бавовняні товари.

В системах взаємозалежних рівнянь кожна залежна змінна представлена як функція інших залежних змінних незалежних та незалежних змінних :

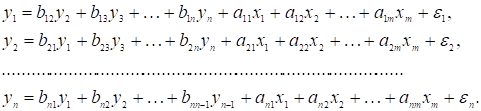(1.9)

Ця система найбільш розповсюджена і отримала назву системи спільних одночасних рівнянь. Її також називають структурною формою моделі. В системі одні й ті ж змінні одночасно є залежними в одних рівннянх і незалежними в інших.

Розглянемо, наприклад, макроекономічну модель з трьох рівнянь:

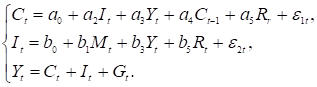
де  – сукупне споживання,  – повні капітальні вкладення,  – валовий національний продукт,  – короткострокова відсоткова ставка,  – обсяг грошового обороту,  – урядові витрати.

Тут , ,  – ендогенні змінні, а , , ,  – пояснюючі. Розвязок може бути знайдений лише одночасним рішенням трьох рівнянь. останнє рівняння – тотожність, але його можна розглядати як звичайне рівняння з усіма коефіцієнтами рівними одиниці.

1.4 Статистична база економетричних моделей

Будь-яке економетричне дослідження завжди поєднує теорію (математичні моделі) і практику (статистичні дані). За допомогою моделей описують і пояснюють процеси, що вивчаються, а статистичні дані використовують для побудови та обґрунтування моделей. Без конкретних кількісних даних, що характеризують функціонування економічного об'єкта, не завжди можна визначити практичну значущість певної моделі.

Економічні дані звичайно поділяють на два види: перехресні дані та часові ряди. Перехресними є дані за якимось економічним показником, що отримані для різних однотипних об'єктів (фірм, регіонів). Причому дані отримано в один і той самий момент часу або часова приналежність несуттєва. Часові ряди характеризують один і той самий об'єкт, але в різні моменти часу. Наприклад, дані бюджетних досліджень населення в певний момент часу є перехресними, а динаміка рівня інфляції за певний період відображується часовими рядами. Послідовні значення часових рядів можуть бути пов'язані між собою певними залежностями: спостерігаються деякі закономірності у відхиленнях від загальної тенденції розвитку чи виявляються часові зсуви показників (часові лаги). Тому методи обробки таких даних дещо відрізняються від методів, що застосовуються для обробки перехресних даних.

При підготовці статистичних даних для роботи з певною моделлю необхідно забезпечити відповідність цих даних моделі та спільну методичну базу для їх оцінювання. Дані мають утворювати взаємно узгоджений набір.

Складання математичної моделі, що відбиває розвиток того чи іншого економічного процесу, починається з оцінки даних. Всі методи регресійного аналізу використовують апарат математичної статистики, який вимагає від вихідних даних, щоб вони були порівняні і однорідні, а для виявлення закономірності, крім цього, були стійкими і кількість спостережень була досить великою. Невиконання одного з цих вимог робить безглуздим застосування математичного аналізу.

Порівнянність передбачає формування всіх рівнів ряду спостережень за однією і тією ж методикою, використання однакових одиниць вимірювання та за можливості кроку спостережень. У часових рядах вимога однакового кроку за часом є обов'язковою.

Однорідність досягається відсутністю сильних зламів, а також нетипових аномальних спостережень. При пошуку закономірностей буває доцільно відкинути частину попередніх даних, якщо вони відображають закономірність минулого розвитку, яка вже втратила силу. Наявність аномальних (різко виділяються) спостережень призводить до спотворення результатів. Формально аномальність проявляється як сильний стрибок з наступним приблизними відновленням попереднього рівня. Прикладом такого спостереження може служити значення курсу долара, зафіксованого в «чорний вівторок».

Вимога повноти даних обумовлюється тим, що закономірність може виявитися лише при наявності мінімально допустимого обсягу спостережень. Достатня кількість спостережень визначається залежно від мети дослідження. У часових рядах, наприклад, якщо мета дослідження – побудова моделі динаміки з метою подальшого прогнозу, число рівнів вихідного динамічного ряду має бути не менше семи.

Стійкість характеризує переважання закономірності над випадковістю в зміні рівнів ряду. Діаграма розсіювання дозволяє зробити візуальний аналіз емпіричних даних. Однак існують і більш точні, теоретично обґрунтовані методи виявлення закономірного зв'язку між випадковими змінними Y і X. Найбільш поширеним з них є метод Фостера-Стюарта (СР.01). Він дозволяє не тільки встановити наявність тенденцій у зв'язку кількісних ознак Y і X, а й перевірити гіпотезу про сталість дисперсії випадкового обурення.

Отже, формуючи сукупність спостережень, слід забезпечити порівнянність даних у просторі та часі. Це означає, що дані вхідної сукупності повинні мати:

-                однаковий ступінь агрегування;

-                однорідну структуру одиниць сукупності;

-                одні й ті самі методи розрахунку показників у часі чи просторі;

-                однакову періодичність обліку окремих змінних;

-                порівнянні ціни та однакові інші зовнішні економічні умови.

Висновки, які можна зробити в результаті економетричного моделювання, цілком зумовлені якістю вхідних даних, а саме їх повнотою та достовірністю.

САМОСТЙНА РОБОТА

1. Дослідити особливості застосування методу Фостера-Стюарта з метою виявлення закономірного зв’язку між випадковими змінними [3, с. 33-36].

В таблиці 1.1 наведено динаміку зростання прибутку деякої фірми за останні n років у % до базового (нульового) року. Встановити чи спростувати за допомогою методу Фостера-Стюарта наявність тенденції у зв’язку прибутку від номеру року (№ варіанту відповідає порядковому номеру студента у списку групи).

2. Розглянути метод характерних середніх, що дозволяє вибрати найкращу функцію регресії з 9 можливих [3, с. 44-47].

Визначити найкращу функцію регресії методом характерних середніх із дев’яти можливих функцій, що описують зв'язок прибутку фірми від номеру року (табл. 1.1).

Таблиця 1.1

№ Рік	Прибуток фірми по роках, тис. грн.
	1	2	3	4	5	6	7	8	9	10
1	104.3	112.8	118.4	130.1	148.7	172.5	202.6	220.8	250.4	295.9
2	110.1	130.4	158.3	170.7	198.5	230.9	280.6	320.6	360.4	392.8
3	115.4	132.7	161.2	181.4	214.5	241.2	272.9	301.4	320.5	350.4
4	109.2	122.8	141.5	160.6	187.4	222.5	270.4	304.5	331.7	362.8
5	112.0	133.4	149.7	162.5	183.2	201.9	232.6	259.6	280.4	312.0
6	121.5	142.4	159.1	173.6	190.9	212.2	237.8	263.4	287.5	-
7	115.0	132.5	146.4	159.8	172.4	191.6	210.3	228.4	250.0	-
8	110.5	124.6	142.4	162.5	181.7	198.9	215.6	240.4	265.5	-
9	114.0	128.5	151.2	173.4	195.8	220.6	248.7	280.0	310.4	-
10	125.4	141.2	168.4	181.3	197.6	211.9	228.3	248.1	266.0	-
11	118.6	132.4	152.7	168.9	181.4	196.8	213.5	235.5	-	-
12	122.0	141.6	156.4	179.8	192.1	216.7	248.0	270.4	-	-
13	128.1	154.2	182.5	203.4	221.9	243.4	272.5	300.0	-	-
14	120.0	135.6	151.2	170.4	188.2	206.5	225.0	250.5	-	-
15	114.1	128.3	150.4	166.2	183.0	200.6	215.3	240.0	-	-
16	120.5	132.4	151.2	172.8	193.4	212.8	240.1	272.4	300.0	-
17	130.4	151.2	174.4	196.8	220.3	252.4	274.5	290.4	315.0	-
18	141.2	170.4	191.3	220.8	254.2	282.1	305.4	332.9	370.5	-
19	118.3	132.6	149.4	170.2	190.5	221.4	248.3	275.0	300.0	-
20	122.8	145.6	164.3	179.7	196.4	212.5	234.6	252.7	284.5	-
21	115.4	132.6	148.3	164.8	185.1	201.4	220.3	241.7	270.0	296.5
22	109.3	124.5	140.0	157.3	172.7	191.9	207.3	223.9	240.5	260.0
23	114.2	128.3	147.4	160.7	175.0	194.8	210.0	228.4	245.7	265.5
24	118.0	132.1	145.2	165.3	190.4	221.7	243.4	270.5	294.8	320.4
25	132.4	150.2	171.8	198.3	230.0	261.2	293.4	321.2	348.3	375.2
26	122.8	141.2	157.4	172.8	194.7	218.3	245.8	270.1	297.3	330.0
27	111.0	132.4	152.7	170.6	188.5	199.9	220.0	241.4	262.5	-
28	117.4	138.1	160.2	181.4	203.0	228.1	255.3	282.7	320.0	-
29	124.2	150.0	178.3	210.7	251.2	290.7	331.8	372.4	410.8	-
30	119.4	140.3	170.5	190.8	214.1	242.7	273.2	302.6	350.4	-
31	115.6	126.2	138.1	150.4	163.5	180.2	200.0	-	-	-
32	120.0	141.2	160.3	188.4	210.3	235.3	260.0	-	-	-
33	112.4	117.4	130.3	150.2	177.3	204.0	223.7	-	-	-
34	107.2	121.3	140.4	162.5	180.7	201.2	225.6	-	-	-
35	115.6	137.2	155.8	174.6	198.9	215.4	240.3	-	-	-
36	112.8	123.4	137.7	154.0	171.2	193.6	210.8	-	-	-
37	113.4	132.5	154.6	178.2	199.4	230.4	262.5	-	-	-
38	107.3	120.5	134.6	152.7	165.4	184.6	202.5	-	-	-
39	114.1	123.7	138.6	154.2	170.6	190.2	210.6	-	-	-
40	110.5	122.7	137.4	150.2	164.3	180.2	197.5	-	-	-
41	112.4	120.8	132.4	141.2	150.4	162.3	177.5	-	-	-
42	108.4	121.2	137.3	152.8	171.4	192.3	215.6	-	-	-
43	120.4	148.5	172.4	198.5	227.4	258.7	286.5	-	-	-
44	127.5	141.3	158.6	177.4	196.8	213.4	240.1	-	-	-
45	121.4	147.3	173.5	199.6	227.3	252.4	280.0	-	-	-
46	115.3	128.3	142.7	160.4	180.5	199.6	227.4	-	-	-
47	112.8	127.3	141.4	159.7	173.8	197.6	215.0	-	-	-
48	116.4	127.4	143.7	162.5	187.4	205.6	230.4	-	-	-
49	108.6	121.6	136.4	158.3	176.4	198.2	218.6	-	-	-
50	110.4	127.6	142.4	160.2	182.6	202.7	225.0	-	-	-