ЛЕКЦІЯ 3. «Методи побудови парної лінійної регресії»

Анотація

«Істинне» рівняння регресії. Парна регресія. Систематична та випадкова складові. Метод найменших квадратів (МНК). Оцінки найменших квадратів. Умови Гаусса-Маркова. Гетероскедастичність та гомоскедастичність. Властивості оцінок параметрів регресійного рівняння: незміщеність, обґрунтованість, ефективність та інваріантність. Множинна регресія. Специфікація багатофакторної моделі. Мультиколінеарність. Помилки специфікації множинної регресії. Практичні наслідки мультиколінеарності. Ознаки мультиколінеарності та методи її усунення.

 

1.1    Регресійна задача для випадку одного фактора

Після кореляційного аналізу проводиться регресійний аналіз, основною задачею якого є дослідження залежності змінної, що вивчається, від різних факторів та відображення їх взаємозв’язку у формі регресійної моделі.

Нехай маємо набір значень двох змінних  – пояснювальна змінна та  – пояснююча змінна, кожна з яких містить n спостережень. Нехай між ними теоретично існує деяка лінійна залежність

                                            ,                                     (3.1)

Це рівняння будемо називати «істинним» рівнянням регресії.

Однак в дійсності між змінними спостерігається не настільки жорсткий зв'язок. Окремі спостереження  будуть відхилятися від лінійної залежності в силу різних причин. Враховуючи можливі відхилення лінійне рівняння зв’язку двох змінних (парну регресію) представимо у вигляді

                                              ,                                      (3.2)

де      – постійна величина (або вільний член рівняння);

          – коефіцієнт регресії, що визначає нахил лінії. вздовж якої розсіяні дані спостереження;

          – випадкова змінна (випадкова складова, залишок або збурення).

Випадкова складова відображає той факт, що зміна  буде неточно описуватися зміною , оскільки присутні інші фактори, невраховані в даній моделі. Таким чином в рівнянні (3.2) значення кожного спостереження  представлено як сума двох частин – систематичної  та випадкової . В свою чергу систематичну частину можна представити у вигляді рівняння, коефіцієнти якого і підлягають оцінюванню

                                                  .                                          (3.3)

Можна сказати, що загальним моментом для будь-якої економетричної моделі є розбиття залежної змінної на дві частини – пояснену та випадкову.

 

1.2    Оцінка параметрів парного регресійного рівняння

Для оцінки параметрів регресійного рівняння найбільш часто використовують метод найменших квадратів.

Метод найменших квадратів дає оцінки, що мають найменшу дисперсію в класі всіх лінійних оцінок, якщо виконуються передумови нормальної лінійної регресійної моделі. МНК мінімізує суму квадратів відхилень значень , що фактично спостерігаються, від модельних значень .

Не доцільно знаходити параметри економетричної моделі, мінімізуючи суму лінійних відхилень фактичних витрат на споживання від розрахункових, бо вона може дорівнювати нулю, якщо сума від’ємних і додатних відхилень буде однаковою. Тому мінімізації підлягає сума квадратів відхилень, і величина її залежатиме безпосередньо від розсіювання точок навколо лінії регресії. Оцінки знаходяться шляхом мінімізації суми квадратів

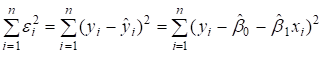                             .                      (3.4)

по всіх можливих  та  при заданих значеннях  та . Задача зводиться до математичної задачі пошуку точки мінімуму функції двох змінних, яка знаходиться шляхом прирівнювання до нуля частинних похідних функції по змінних  та

 

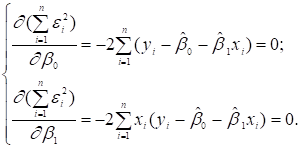                                                         (3.5)

 

 

Виконавши елементарні перетворення, дістанемо систему нормальних рівнянь

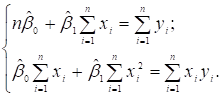                                                                        (3.6)

 

В результаті можемо отримати так звані оцінки найменших квадратів

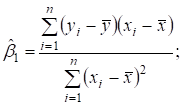                                                                                (3.7)

                                                                                                       

 

1.3    Основні передумови методу найменших квадратів (МНК)

Властивості коефіцієнтів регресії істотним чином залежать від властивостей випадкової компоненти. Для того, щоб регресійний аналіз, що базується на звичайному методі найменших квадратів (МНК) давав найкращі із всіх можливі результати, необхідно щоб виконувалися певні умови, які називаються умовами Гаусса-Маркова, а саме:

1. Математичне сподівання випадкових відхилень  повинно дорівнювати нулеві (незміщеність оцінок):

                                                      .                                              (3.8)

Ця умова вимагає, щоб випадкові відхилення в середньому не впливали на залежну змінну Y, тобто в кожному конкретному спостереженні відхилення  може набувати додатні або від’ємні значення, але не повинно спостерігатися систематичне зміщення відхилень в переважній більшості в бік одного знаку.

Із врахуванням вищесказаного, використовуючи рівняння (3.2), будемо мати:

                                                          (3.9)

2. Дисперсія випадкових відхилень  повинна бути сталою величиною

                                 , .                       (3.10)

Ця вимога передбачає, що не зважаючи на те, що при кожному конкретному спостереженні випадкове відхилення може виявитися відносно великим чи малим, це не повинно складати основу для апріорної причини, тобто причини, що не базується на досвіді, що спонукала б велику похибку.

Моделі, для яких виконується умова (3.10), називають гомоскедастичними (рівнозмінними). Моделі, для яких не виконується умова (3.10) (), називають гетероскедастичними.

Величина , звичайно, невідома і одна з задач регресійного аналізу полягає в оцінці стандартного відхилення випадкової складової.

3. Випадкові відхилення  та ,  повинні бути незалежними одне від одного.

Виконання цієї умови припускає, що між будь-якими випадковими відхиленнями відсутній систематичний зв’язок, тобто величина та знак будь-якого випадкового відхилення не буде являтися причиною величини та знаку будь-якого іншого випадкового відхилення. Цю умову можна записати так

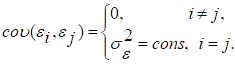                                                                    (3.11)

Тут  є математичний запис коваріаційного (кореляційного) моменту.

4. Випадковий вектор відхилень  повинен бути незалежним від регресорів  матриці .

Ця умова виконується автоматично, коли пояснюючі змінні  не є стохастичними величинами в заданій моделі.

,

бо , а  ( не є випадковою величиною).

А також незалежні змінні моделі повинні утворювати лінійно незалежну систему векторів, або, іншими словами, незалежні змінні не повинні бути мультиколінеарними, тобто :

                                                                                   (3.12)

                                               .

де     Xk – k-й вектор матриці пояснювальних змінних; Xj – j-й вектор цієї матриці пояснювальних змінних X,  .

Поряд з умовами гауса-Маркова зазвичай також припускається, що компоненти  випадкового вектора  повинні мати нормальний закон розподілу .

Тоді випадковий вектор  буде мати нормальний закон розподілу виду .

З теорії ймовірностей відомо (доведено в теоремі Гаусса-Маркова), що коли виконуються перелічені передумови, то отримані за допомогою МНК оцінки параметрів регресійного рівняння є незміщеними, обґрунтованими, ефективними та інваріантними.

Наявність таких властивостей оцінок гарантує, що останні не мають систематичної похибки (незміщеність), надійність їх підвищується зі збільшенням обсягу вибірки (обґрунтованість), вони є найкращими серед інших оцінок параметрів, лінійних відносно ендогенної змінної (ефективність). Крім того, оцінка перетворених параметрів (оцінка функції від параметра) може бути отримана в результаті аналогічного перетворення оцінки параметра (інваріантність).

Зокрема, якщо порушується третя передумова МНК (за наявності автокореляції чи гетероскедастичності), то отримані за цим методом оцінки втрачають властивість ефективності, хоча залишаються незміщеними та обґрунтованими. Якщо порушується четверта передумова, тобто між змінними існують мультиколінеарні зв’язки, це призводить до зміщення МНК-оцінок. Застосування моделей, що мають зміщені чи неефективні оцінки, втрачає сенс.

 

1.4    Загальна лінійна множинна економетрична модель

На будь-який економічний показник Y, як правило, впливає не один, а декілька факторів (регресорів) . Так, наприклад, попит населення на певний товар буде визначатися не тільки ціною на нього, але й цінами на його замінники, доходами споживачів й іншими факторами. У низці досліджень аналізується зв’язок доходу працівника певної галузі виробництва з його рівнем освіти, віком, стажем роботи в цій галузі.

В подібних випадках маємо справу з множинною лінійною моделлю (регресією), що описує взаємний зв’язок між залежною змінною Y та регресорами  і яку можна подати такому вигляді:

                                                    (3.13)

Цей математичний запис інформує про функціональну залежність умовного математичного сподівання залежної змінної Y від m регресорів (незалежних, пояснюючих) змінних Х.

Отже, постає задача виявлення статистичного взаємозв’язку між Y та Х.

Загальний запис теоретичної лінійної множинної регресії може бути зроблений в такому вигляді:

                       ,             (3.14)

де      – теоретичні коефіцієнти регресії (часткові коефіцієнти) або параметри теоретичної регресії, які характеризують реакцію залежної змінної   на зміну кожного регресора  ;

 – вільний член, який визначає значення  за умови, коли значення регресорів дорівнюють нулеві;

  – значення -го регресора при і-ому спостереженні;

 – випадковий збудник при і-ому спостереженні.

Для однозначного визначення параметрів  моделі (3.14) необхідно, щоб виконувалась нерівність

де     n – число спостережень;

m – число регресорів в моделі.

У векторно-матричній формі теоретичну модель (3.14) можна подати так:

                                                                                             (3.15)

де

 

 

 

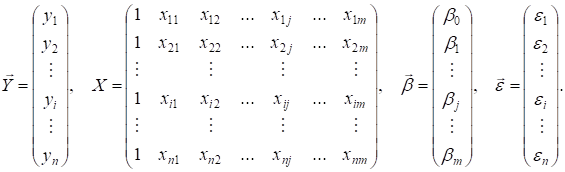
Компоненти  вектора  є величинами сталими (), але невідомими. Їх необхідно оцінити шляхом обробки вибірки, а тому надалі будемо мати справу із емпіричною моделлю, яка є прообразом теоретичної (3.14), (3.15):

                                                                                            (3.16)

Компоненти  вектора  є статистичними оцінками компонент  теоретичного вектора  лінійної множинної регресії (3.15), а компоненти  вектора похибок  – статистичні оцінки випадкових збудників  вектора .

Якщо теоретичний вектор  є величиною сталою і нам невідомою, то емпіричний вектор  ми можемо визначити шляхом обробки статистичної інформації вибірки обсягом n. Враховуючи те, що вибірка складає лише незначну частину генеральної сукупності (n≤N), то інформація, яку одержимо при статистичній обробці, про регресори Xj моделі буде не повною і для кожної іншої вибірки буде потерпати певні зміни. Отже, компоненти  емпіричного вектора  будуть містити елемент випадковості. Таким чином, , як і сам вектор , будуть випадковими величинами, які мають певні закони розподілу ймовірностей із відповідними числовими характеристиками.

Із вище наведеного можемо тепер стверджувати, що  є статистичною оцінкою для теоретичного вектора . А тому постають питання математичної статистики: зміщена чи незміщена ця статистична оцінка; в якому довірчому інтервалі із заданою надійністю γ можуть перебувати теоретичні компоненти (параметри)  і сама функція регресії; як здійснити перевірку на статистичну значущість теоретичних параметрів  по заданому рівню значущості α.

Для вирішення цих питань нам необхідно визначити числові характеристики для параметрів  (j=0,1,2,...,m) і для самої функції регресії, використовуючи при цьому елементи матричної алгебри як інструментарію, застосовуючи який ми можемо без громіздких викладок отримати необхідні результати.

Оцінка параметрів моделі множинної регресії проводиться аналогічно (3.4-3.7) за допомогою методу найменших квадратів. Формула для розрахунків параметрів регресійного рівняння у векторно-матричній формі :

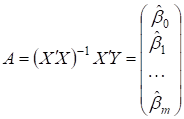                                            .                                 (3.17)

 

 

1.5    Специфікація множинної моделі. Проблема мультиколінеарності

Маючи на увазі, що вибір аналітичної форми економетричної моделі не може розглядатись без конкретного переліку незалежних змінних, специфікація моделі передбачає добір чинників для економетричного дослідження.

При побудові моделі множинної регресії відбір найбільш істотних факторів, що впливають на результативну ознаку, проводиться на основі якісного, теоретичного аналізу у поєднанні з використанням статистичних прийомів. При цьому в процесі такого дослідження можна кілька разів повертатись до етапу специфікації моделі, уточнюючи перелік незалежних змінних та вид функції, що застосовується. Адже коли вид функції та її складові не відповідають реальним залежностям, то йдеться про помилки специфікації.

Помилки специфікації моделі можуть бути трьох видів:

1)  ігнорування істотної пояснюючої змінної при побудові економетричної моделі;

2)  введення до моделі незалежної змінної, яка не стосується вимірю­ваного зв’язку;

3)  використання не відповідних математичних форм залежності.

При цьому порівняльний аналіз та відбір факторів до регресії може здійснюватися на основі кореляційного аналізу.

Одна з передумов застосування методу найменших квадратів до оцінювання параметрів лінійних багатофакторних моделей – відсутність лінійних зв’язків між незалежними змінними моделі. Якщо такі зв’язки існують, то це явище називають мультиколінеарністю.

Суть мультиколінеарності полягає в тому, що в багатофакторній регресійній моделі дві або більше незалежних змінних пов’язані між собою лінійною залежністю або, іншими словами, мають високий ступінь кореляції:

                                                                                        (3.18)

Наявність мультиколінеарності створює певні проблеми при розробці моделей. Насамперед, визначник матриці спостережень наближається до нуля, і оператор оцінювання за звичайним МНК стає надзвичайно чутливий до похибок вимірювань і похибок обчислень. При цьому МНК-оцінки можуть мати значне зміщення відносно дійсних оцінок узагальненої моделі, а в деяких випадках можуть стати взагалі беззмістовними.

Передусім потрібно зрозуміти природу мультиколінеарності.

Наприклад, коли вивчається залежність між ціною акції, дивідендами на акцію та отриманим прибутком на акцію, то дивіденди та отриманий прибуток на одну акцію мають високий ступінь кореляції. Іншими словами, виникає ситуація, коли два колінеарних фактори змінюються в одному напрямку У такому разі майже неможливо оцінити вплив кожного з них на досліджуваний показник.

З’ясуємо, до яких наслідків може призвести мультиколінеарність. Це одне з найважливіших питань, яке потрібно зрозуміти при розробці економетричних моделей.

Практичні наслідки мультиколінеарності:

-        мультиколінеарність незалежних змінних (факторів) призводить до зміщення оцінок параметрів моделі, які розраховуються за МНК. На основі цих оцінок неможливо зробити конкретні висновки про результати взаємозв’язку між показником і факторами;

-        збільшення дисперсії та коваріації оцінок параметрів, обчислених за методом найменших квадратів;

-      збільшення довірчого інтервалу (оскільки збільшується середній квадрат відхилення параметрів);

-      незначущість t-статистик.

Мультиколінеарність не є проблемою, якщо єдиною метою регресійного аналізу є прогноз (оскільки чим більше значення R2, тим точніший прогноз). Якщо метою аналізу є не прогноз, а дійсне значення параметрів, то мультиколінеарність перетворюється на проблему, оскільки її наявність призводить до значних стандартних похибок оцінок параметрів.

Виявлення мультиколінеарності є лише частиною справи. Інша частина – проблема її усуненння. Безпомилкових і абсолютно правильних порад немає, оскільки мультиколінеарність є прикладною проблемою.

Звичайно, усе залежить від ступеня мультиколінеарності, однак у будь-якому разі можна запропонувати кілька простих методів усунення мультиколінеарності:

1)    використання додаткової або первинної інформації;

2)    об’єднання інформації;

3)    відкидання змінної з високою кореляцією;

4)    перетворення даних (використання перших різниць);

5)    збільшення кількості спостережень.

Які поради спрацюють на практиці, залежить від істотності проблеми та її характеру. Якщо переліченими методами не вдається усунути мультиколінеарність, то для оцінювання параметрів багатовимірної моделі доцільно застосувати метод головних компонентів.