ЛЕКЦІЯ 10. «Системи одночасних економетричних
рівнянь»
Анотація
Системи
одночасних економетричних рівнянь. Ендогенні та
екзогенні змінні. Структурна та зведена форми економетричної
моделі. Повна економетрична модель. Ідентифікованість моделі. Неідентифікована, точно (строго) ідентифікована
(ототожнена), над ідентифікована моделі. Необхідна та достатня умови ідентифікованості системи. Непрямий метод найменших
квадратів. Двокроковий та трикроковий
методи найменших квадратів. Прогноз і загальні довірчі інтервали.
10.1 Системи
одночасних економетричних рівнянь
Наявність прямих і зворотних
зв’язків між економічними показниками вимагає
побудови економетричної моделі на основі системи
рівнянь.
Приклад 10.1. Нехай треба побудувати економетричну модель, яка характеризує обсяг національного
доходу залежно від виробничих ресурсів: основних виробничих фондів, робочої
сили і матеріальних ресурсів. У такому разі доцільно будувати економетричну модель на основі системи одночасових
структурних рівнянь:
![]()
![]()
![]()
де ![]() – внутрішній валовий продукт;
– внутрішній валовий продукт;
![]() – основні виробничі фонди;
– основні виробничі фонди;
![]() – робоча сила;
– робоча сила;
![]() – матеріальні ресурси;
– матеріальні ресурси;
![]() – період часу.
– період часу.
Запишемо два перші рівняння
аналітично:
![]()
![]()
![]()
де ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() – параметри
моделі,
– параметри
моделі, ![]() ,
, ![]() – залишки.
– залишки.
Отже, економетрична
модель складається з трьох одночасових рівнянь, два
перших є регресійними, а третє – тотожність. Оскільки вони описують
економічні процеси, які відбуваються одночасно, то всі ці рівняння повинні мати
спільний розв’язок.
Розглядаючи наведений приклад,
можна сказати, що економетрична модель містить
сукупність рівнянь, які описують зв’язки між економічними показниками.
Взаємозв’язки між змінними можуть мати стохастичний і детермінований характер.
Стохастичні зв’язки реалізуються з деяким рівнем імовірності і описуються
регресійними рівняннями. Детерміновані співвідношення виражаються тотожностями і не містять випадкових величин.
Системи одночасових структурних рівнянь, як правило, включають лінійні рівняння. Нелінійність зв’язків здебільшого апроксимується лінійними
співвідношеннями. Динаміка економічних зв’язків
враховується за допомогою часових лагів, або лагових
змінних.
Запишемо економетричну
модель на основі системи одночасових рівнянь:
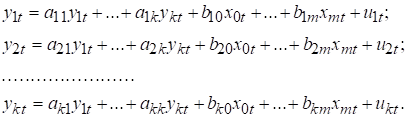 (10.1)
(10.1)
У цій моделі ![]() =1. Окремі коефіцієнти
=1. Окремі коефіцієнти ![]() ...,
..., ![]() ,
, ![]() ...,
..., ![]() можуть дорівнювати
нулю, якщо відповідна змінна не входить до рівняння. Залишки
можуть дорівнювати
нулю, якщо відповідна змінна не входить до рівняння. Залишки ![]() , де s = 1,2, ..., k, також можуть дорівнювати нулю, якщо відповідне рівняння є
тотожністю. Систему (10.1) можна переписати в матричній формі
, де s = 1,2, ..., k, також можуть дорівнювати нулю, якщо відповідне рівняння є
тотожністю. Систему (10.1) можна переписати в матричній формі
![]() (10.2)
(10.2)
де Y – вектор ендогенних залежних
змінних;
X – матриця екзогенних
пояснювальних змінних;
u – вектор залишків;
A – матриця коефіцієнтів при
змінних Y розміром k k;
B – матриця коефіцієнтів при
змінних X розміром k m;
Змінні, які містяться в правій
частині системи рівнянь, є наперед заданими (вхідними) і називаються екзогенними, а змінні, які містяться в
лівій частині, знаходяться в результаті реалізації моделі і називаються ендогенними. Отже, змінна у є ендогенною для одного рівняння і
одночасно екзогенною для іншого.
Означення 10.1: Економетрична
модель у вигляді (10.1) безпосередньо відображає структуру зв’язків
між змінними і тому називається структурною формою економетричної
моделі.
Структурна форма економетричної моделі описує одно- та багатосторонні
стохастичні причинні співвідношення між економічними величинами в їх
безпосередньому вигляді. Вона містить усю суттєву інформацію про залежності між
економічними явищами та процесами. Кожне співвідношення такої системи (рівняння
чи тотожність) має певну економічну інтерпретацію.
Економетрична модель
називається повною, якщо:
а) вона охоплює змінні, що
суттєво впливають на спільно залежні змінні, а вектор залишків має
випадковий характер;
б) містить стільки рівнянь,
скільки в ній є спільно залежних змінних, тобто кожна залежна змінна
пояснюється окремим рівнянням;
в) система рівнянь має
однозначний розв'язок відносно спільно залежних змінних, тобто матриця (E – A) в моделі (10.2) невироджена (має відмінний від нуля визначник).
Повна модель застосовується у
випадках, коли необхідно кількісно описати економічне явище чи процес або
спрогнозувати їх розвиток.
Якщо економетрична
модель застосовується не для аналізу системи, а для передбачення чи оцінювання
параметрів, структурна форма моделі неприйнятна. Алгебраїчними перетвореннями
систему структурних рівнянь зводять до форми, у якій кожне рівняння містить
лише одну ендогенну змінну, яка є функцією від екзогенних змінних. Така форма
рівнянь називається зведеною.
Зведену форму рівнянь можна
назвати скороченою. Це пов'язано з тим, що при певних перетвореннях
багато окремих економічних залежностей можуть бути
виключені з розгляду, а отже, загальна кількість рівнянь може скоротитися.
Внаслідок таких перетворень
зведена форма рівнянь, на відміну від структурної, не має ні безпосередньої, ні
будь-якої економічної інтерпретації. Рівняння у зведеній формі дають змогу
передбачити, як зміниться значення ендогенної змінної, якщо змінюватимуться
значення екзогенних змінних, однак па підставі цих рівнянь неможливо пояснити,
як і чому це відбувається. Саме через це зведену форму рівнянь називають також прогнозною.
Розв’яжемо систему рівнянь
(10.1) відносно Y і дістанемо систему
виду:
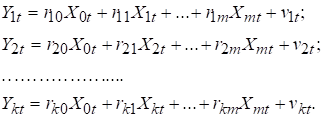 (10.3)
(10.3)
У матричній формі систему цих
рівнянь можна переписати так:
![]() (10.4)
(10.4)
Матриця оцінок параметрів R має вигляд:
![]() (10.5)
(10.5)
де E – одинична матриця.
Щоб показати справедливість
співвідношення (10.5), розв’яжемо систему рівнянь (10.2) відносно Y:
Y – AY = BX + u; (10.6)
(E – A)Y = BX + u; (10.7)
Y = (E – A)–1BX + u. (10.8)
Враховуючи, що Y = RX + v, R = (E – A)–1B.
Вектор залишків ![]() є лінійною комбінацією
залишків
є лінійною комбінацією
залишків ![]() .
.
Означення 10.2: Економетрична
модель, яка записується системою рівнянь (10.3), називається зведеною формою моделі.
Оскільки економетрична
модель складається з системи одночасових рівнянь, то
постає запитання: чи можна застосувати для оцінювання параметрів кожного
рівняння або системи в цілому ті методи, які були розглянуті в попередніх
розділах?
10.2 Проблеми ідентифікації системи рівнянь
Проблеми чисельної оцінки
параметрів в структурній формі і можливість перетворення структурної форми на
зведену тісно пов’язані з поняттям ідентифікованості
моделі.
Щоб забезпечити необхідну
якість оцінок параметрів (незміщеність, ефективність
і обґрунтованість), намагаються па підставі оцінених параметрів скороченої
(зведеної) форми системи рівнянь отримати оцінки параметрів структурної форми.
Однак тут виникає проблема однозначних залежностей
між параметрами: при поверненні від скороченої форми моделі до структурної
(обернені перетворення) можна отримати єдине значення шуканого параметра чи
кілька різних значень або взагалі не мати змоги отримати жодного.
Щоб передбачити можливі
варіанти розв'язання задачі оцінювання параметрів системи одночасних рівнянь,
необхідно попередню дослідити модель, а саме перевірити ідентифікованість
системи. Під проблемою ідентифікації розуміють можливість чисельної оцінки
параметрів структурних рівнянь за оцінками коефіцієнтів зведених рівнянь.
Означення 10.3: Якщо ніяка лінійна комбінація рівнянь
структурної форми не може привести до рівняння, що має ті самі змінні, як і
деяке рівняння в структурній формі, то модель буде ідентифікованою.
Економетрична модель, задана
системою одночасних рівнянь, називається точно
(строго) ідентифікованою (ототожненою),
якщо однозначно можна отримати оцінки її параметрів на основі оцінених
параметрів зведеної моделі.
Надідентифікованою (переототожненою) називається така модель, що для деяких її параметрів можна
отримати кілька кількісних значень на підставі параметрів зведеної форми.
Для ідентифікації моделей
зведена форма визначається однозначно за допомогою співвідношень (10.3).
Матриця E – A завжди
невироджена. Умова ідентифікації має перевірятися для кожного рівняння системи.
Необхідна умова ідентифікації системи – справедливість нерівності для кожного рівняння моделі (10.1):
![]() (10.10)
(10.10)
де ![]() – кількість залежних ендогенних змінних, які входять в s-те рівняння структурної форми;
– кількість залежних ендогенних змінних, які входять в s-те рівняння структурної форми;
m – загальна кількість
екзогенних змінних моделі;
![]() – кількість екзогенних змінних, які входять в s-те рівняння структурної форми моделі.
– кількість екзогенних змінних, які входять в s-те рівняння структурної форми моделі.
Число екзогенних змінних, які
не входять у s-те рівняння
структурної форми, дорівнює ![]() .
.
Означення 10.4: Якщо для всіх рівнянь моделі (10.1)
співвідношення (10.10) виконується як рівність, то система рівнянь є точно ідентифікованою.
Означення 10.5: Якщо для всіх
рівнянь моделі співвідношення (10.10) виконується як нерівність, то система
рівнянь є надідентифікованою.
Можна показати, що необхідною
умовою ідентифікації певного рівняння є: число змінних, які виключені з
рівняння, має дорівнювати числу рівнянь моделі мінус одиниця.
Альтернативна умова ідентифікації була записана нами в
(10.10):
![]()
яка потребує, щоб число виключених із рівняння
екзогенних змінних було не меншим, ніж число ендогенних змінних мінус одиниця.
Необхідною і достатньою умовою ідентифікованості є: у моделі, що містить k рівнянь відносно k ендогенних
змінних, умова ідентифікованості виконується тоді і
тільки тоді, коли ранг матриці, складеної з виключених з даних рівнянь змінних,
але таких, що містяться в інших рівняннях системи, дорівнює k-1.
10.3 Непрямий
метод найменших квадратів (НМНК)
Можна
довести, що застосування звичайного МНК до рівнянь структурної форми системи
рівнянь призводить до отримання зміщених оцінок параметрів через корельованість (залежність) змінних і залишків моделі, що є
порушенням однієї з передумов застосування МНК. Перехід від структурної форми
моделі до скороченої є одним із способів, що усуває проблему корельованості, однак породжує іншу, а саме проблему ідентифікованості окремих рівнянь системи, а також системи
загалом.
Залежно
від розв'язання цієї проблеми, тобто після перевірки умови ідентифікованості
кожного рівняння системи, застосовують такі методи
оцінювання параметрів системи:
1) якщо кожне рівняння системи точно
ідентифіковане, то параметри зведеної моделі оцінюють непрямим методом найменших квадратів (НМНК); ідея методу полягає в
тому, щоб від структурної форми перейти до зведеної, звичайним МНК оцінити
параметри останньої й оберненим перетворенням отримати оцінки параметрів
структурної форми;
2) усунути кореляцію між змінними та
залишками моделі можна також за допомогою методу
інструментальних змінних, ідея якого полягає в тому, щоб змінні, що
корелюють із залишками, замінити іншими – інструментальними, які тісно
пов'язані з незалежними змінними моделі, але зовсім не пов'язані з її
залишками;
3) якщо рівняння структурної форми моделі надідентифіковані, то параметри моделі оцінюють за
допомогою двокрокового методу найменших квадратів (2МНК), що
передбачає виконання двох етапів:
а)
перший – ендогенні змінні «звільняють» від стохастичних залишків;
6)
другий – оцінені рівняння підставляють у структурну систему рівнянь, до
яких потім застосовують звичайний МНК;
4) трикроковий метод
найменших квадратів для одночасного оцінювання всіх рівнянь системи за
певних обставин ефективніший порівняно з непрямим і двокроковим
МНК.
Оскільки
на основі звичайного МНК неможливо отримати якісні оцінки параметрів системи
одночасних рівнянь, варто скористатися іншими методами оцінювання параметрів.
Одним із них є непрямий метод найменших
квадратів, що ґрунтується на використанні зведених рівнянь.
Він
складається з двох процедур. Спочатку застосовується 1МНК для оцінки параметрів
кожного рівняння зведеної форми моделі (10.7)–(10.8). Основна особливість такої
форми полягає в тому, що її здобуто в результаті розв’язування структурної
системи рівнянь відносно поточних значень ендогенних змінних, і зведена форма
виражає їх як функції всіх інших змінних моделі таким чином, що кожне рівняння
в такій формі має поточне значення тільки однієї ендогенної змінної.
Алгоритм непрямого методу
найменших квадратів.
Крок 1. Перевіряється умова ідентифікованості для кожного рівняння структурної форми
моделі. Якщо кожне рівняння точно індентифіковане, то
переходимо до кроку 2.
Крок 2. Кожне рівняння структурної
форми розв’язується відносно однієї з k
залежних ендогенних змінних моделі, у результаті приходимо до зведеної форми
моделі.
Крок 3. На основі 1МНК визначається
оцінка параметрів окремо для кожного рівняння зведеної форми.
Крок 4. Розраховується оцінка
параметрів рівнянь структурної форми за допомогою співвідношення AR = –B, де A і B
параметри структурних рівнянь, а R –
матриця оцінок параметрів зведеної форми.
Для ілюстрації НМНК розглянемо
кейнсіанську модель формування прибутків:
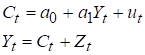 .
.
У зведеній формі ця модель має
вигляд
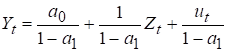 ,
,
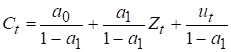 .
.
Позначимо
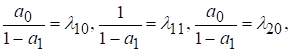
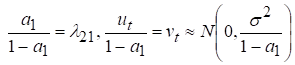
Тоді замість останніх
співвідношень отримаємо
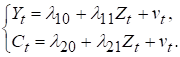
Через те, що обсяг інвестицій ![]() є екзогенною змінною моделі, ця змінна не корелює з випадковим
залишком
є екзогенною змінною моделі, ця змінна не корелює з випадковим
залишком ![]() у зведеній формі
системи рівнянь, а отже, і з залишками
у зведеній формі
системи рівнянь, а отже, і з залишками ![]() останньої системи.
Це означає, що для випадкового члена
останньої системи.
Це означає, що для випадкового члена ![]() виконуються
передумови МНК. Тому оцінки параметрів
виконуються
передумови МНК. Тому оцінки параметрів ![]() , отримані за МНК, будуть
незміщеними, обґрунтованими і ефективними. Знаючи ці оцінки, нескладно
визначити оцінки коефіцієнтів
, отримані за МНК, будуть
незміщеними, обґрунтованими і ефективними. Знаючи ці оцінки, нескладно
визначити оцінки коефіцієнтів ![]() рівняння початкової структурної
системи:
рівняння початкової структурної
системи:
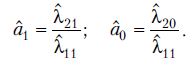
10.4 Оцінювання
параметрів надідентифікованих моделей
Система рівнянь для обчислення оцінок двокроковим методом найменших квадратів запишеться так:
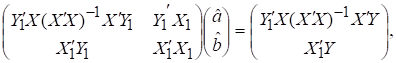
де Y – вектор залежної або ендогенної змінної;
Y1 – матриця
поточних ендогенних змінних, які входять у праву частину рівняння;
X – матриця
всіх пояснювальних або екзогенних змінних;
X1 – матриця
пояснювальних або екзогенних змінних даного рівняння;
![]() – вектор
структурних параметрів, які стосуються змінних матриці Y1;
– вектор
структурних параметрів, які стосуються змінних матриці Y1;
![]() – вектор
структурних параметрів, які стосуються до змінних матриці X1.
– вектор
структурних параметрів, які стосуються до змінних матриці X1.
Тоді оператор оцінювання 2МНК запишеться так:
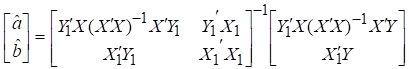 .
.
Дисперсія залишків для кожного рівняння має вигляд:
![]() .
.
Матриця коваріацій
параметрів кожного рівняння визначається на основі співвідношення:
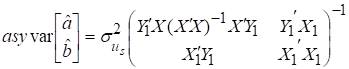 .
.
Розглянуті методи дають змогу оцінювати параметри
окремих рівнянь системи. Кожен з них має переваги та недоліки, однак їх
об'єднує спільна риса – значний обсяг розрахунків при роботі із системами
великої розмірності, тобто із такими, що містять велику кількість рівнянь, а
отже, велику кількість змінних і параметрів. Скорочення обсягу розрахунків стає
особливо актуальним у процесі вивчення швидкоплинних процесів, а також у тому
разі, якщо змінюється пріоритетність окремих незалежних змінних моделі. У цих
випадках краще скористатися методом, що одночасно оцінює параметри всіх рівнянь
системи, зокрема трикроковим методом найменших квадратів (ЗМНК).
Особливістю ЗМНК є те, що при оцінюванні параметрів
системи загалом слід зважати па залежності між окремими рівняннями. Ці
залежності виявляються в тому, що залишки окремих рівнянь корелюють між собою,
тобто загальна матриця коваріацій системи є
недіагональною. У такій ситуації найкращим методом оцінювання є узагальнений метод найменших квадратів
(метод Ейткена). Однак у цьому разі необхідно знати
перше наближення матриці коваріацій. Для рівнянь
множинної регресії з автокорельованими залишками цю
матрицю отримують на підставі залишків моделі, параметри якої оцінено за
звичайним МНК, і вже після обчислення коефіцієнта кореляції коригують загальний
оператор оцінювання параметрів рівняння.
Для систем рівнянь, особливо в разі надідентифікованості окремих рівнянь, краще початкове
наближення матриці коваріацій визначають за
залишками, які отримано в результаті оцінювання параметрів рівнянь за двокроковим МНК. Отже, саме поєднання 2МНК і методу Ейткена дало назву цьому методу.
Трикроковий метод найменших
квадратів (3МНК), на відміну від попередніх, призначений для одночасної оцінки
параметрів всіх рівнянь моделі. Оператор оцінювання 3МНК матиме вигляд:
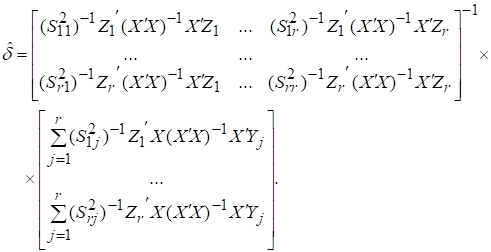
де 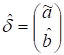 – оцінки
параметрів моделі;
– оцінки
параметрів моделі;
Zs = (Ys Xs), ![]() – Zs
– змінні моделі, які знаходяться в правій частині s-го рівняння;
– Zs
– змінні моделі, які знаходяться в правій частині s-го рівняння;
![]() – дисперсії залишків для кожного рівняння, які є
наближеною оцінкою
– дисперсії залишків для кожного рівняння, які є
наближеною оцінкою ![]() .
.
Щоб застосувати 3МНК на практиці необхідно виконання
таких вимог:
1) розпочинаючи оцінювати параметри моделі,
необхідно вилучити всі тотожності;
2) виключити з системи кожне неідентифіковане
рівняння;
3) за наявності серед рівнянь системи точно
ідентифікованих та надідентифікованих 3МНК доцільно
застосовувати до кожної з груп рівнянь окремо;
4) якщо група надідентифікованих
рівнянь має тільки одне рівняння, то 3МНК перетворюється на 2МНК;
5) якщо матриця коваріацій
для структурних залишків є блочно-діагональною, то вся процедура оцінювання на
основі 3МНК може бути застосована окремо для кожної групи рівнянь, які
відповідають одному блоку.
Точковий прогноз
залежних ендогенних змінних визначається на основі приведеної форми економетричної моделі
![]()
де Xf – вектор
прогнозних екзогенних змінних.
Визначення довірчих інтервалів для цього прогнозу
залежить від методу, за допомогою якого було одержано матрицю ![]() .
.
Довірчі
інтервали для кожної ендогенної змінної задаються співвідношенням
![]()
де ![]() – дисперсія залишків s-го рівняння моделі;
– дисперсія залишків s-го рівняння моделі;
t(a/2) = F(a).
Довірчі інтервали для всіх ендогенних змінних
визначаються так:
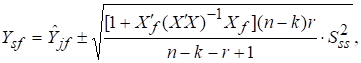
де ![]() – незміщена дисперсія залишків всіх рівнянь моделі.
– незміщена дисперсія залишків всіх рівнянь моделі.
Ці інтервали будуть ширшими, ніж тоді, коли їх
задавати для кожної ендогенної змінної окремо.