ЛЕКЦІЯ 9. «Ідентифікація та
прогноз часових рядів»
Анотація
Динамічний та часовий ряди. Систематичні та випадкові компоненти
часового ряду. Фільтрація компонент часового ряду. Стаціонарність часового
ряду. TS, DS, тренд-сезонні, нелінійні часові ряди. Дослідження автокореляційної
функції часового ряду. Методи
фільтрації сезонної компоненти. Прогнозування тенденції часового ряду за
механічними методами та аналітичними методами. Адаптивні методи прогнозування.
Метод декомпозиції часового ряду. Розрахунок сезонної хвилі.
9.1 Основні поняття і
попередній аналіз рядів динаміки
Спостереження над деяким явищем, характер якого змінюється в
часі, породжує впорядковану послідовність, що називається часовим рядом. У кожен момент часу (або часовий інтервал) значення
досліджуваної величини, що є числовою характеристикою явища, може формуватися
під сукупною дією великого числа чинників як випадкового, так і невипадкового
характеру. Зміна умов розвитку явища веде до ослаблення дії одних чинників і
посилення інших і кінець кінцем до варіювання ознаки, що вивчається, в часі.
Динамічний
ряд – це сукупність спостережень
одного показника, впорядкованих залежно від значень іншого показника, що
послідовно зростають або спадають.
Часовий ряд (time
series) – це ряд динаміки,
впорядкований за часом, або сукупність спостережень економічної величини в
різні моменти часу.
Для аналізу
соціально-економічних показників абсолютні рівні моментальних або інтервальних
часових рядів, а також рівні середніх величин часто доводиться перетворювати на
відносні величини. До найпоширеніших характеристик динаміки розвитку
соціально-економічних процесів та їхні розрахунки відносяться: абсолютний
приріст, коефіцієнти зростання та приросту, темпи зростання та приросту,
середні арифметична, хронологічна тощо.
Існує дві основні мети аналізу
часових рядів:
визначення природи ряду та
прогнозування.
Обидві
ці цілі вимагають, щоб модель ряду була ідентифікованою і більш-менш формально
описаною.
Розгляд реальних ситуацій дозволяє прийти до висновку, що типові часові
ряди можуть бути представлені як декомпозиція із чотирьох структурно утворюючих
елементів:
тренд (Ut),
сезонна компонента (St),
циклічна компонента (Vt) –
коливання відносно тренда з більшою або меншою регулярністю,
випадкова компонента (Et),
тобто
![]() . (9.1)
. (9.1)
Також можуть виділяти і інші компоненти
![]() , (9.2)
, (9.2)
де ![]() ‑ компонента, що забезпечує порівнянність
елементів динамічного ряду,
‑ компонента, що забезпечує порівнянність
елементів динамічного ряду,
![]() ‑ управляюча компонента, за допомогою якої
впливають на значення членів динамічного ряду для формування в майбутньому
бажаної траєкторії.
‑ управляюча компонента, за допомогою якої
впливають на значення членів динамічного ряду для формування в майбутньому
бажаної траєкторії.
Очевидно, реальні дані цілковито не відповідають лише одній із наведених
функцій, тож часовий ряд ![]() ,
, ![]() можна уявити у вигляді
розкладення:
можна уявити у вигляді
розкладення:
![]() ,
, ![]() (9.3)
(9.3)
або різноманітних поєднань окремих функцій. Однак завжди припускають
обов’язкову наявність випадкової складової. Розкладення (декомпозиція) часового
ряду відбувається за такими варіантами моделей:
модель тренду ![]() ,
, ![]() ; (9.4)
; (9.4)
модель сезонності ![]() ,
, ![]() ; (9.5)
; (9.5)
тренд-сезонна модель ![]() ,
, ![]() . (9.6)
. (9.6)
Моделі тренду й сезонності (тренд-сезонні) можуть відображати як відносно
постійну сезонну хвилю (цикл), так і динамічно змінювану залежно від тренду.
Перша форма – (9.3–9.6) належить до адитивних,
друга (![]() ,
, ![]() , (9.7)) – до мультиплікативних
моделей.
, (9.7)) – до мультиплікативних
моделей.
Тренд,
сезонна і циклічна компоненти не є випадковими і називаються систематичними компонентами часового
ряду.
Випадкові чинники не підлягають вимірюванню, але
неминуче супроводжують будь-який економічний процес і визначають стохастичний
характер його елементів. До випадкових чинників можна віднести помилки
вимірювання, випадкові збурення тощо. Деякі часові ряди, наприклад стаціонарні, не мають тенденції та
сезонної складової, кожен наступний рівень їх утворюється як сума середнього
рівня ряду і випадкової (додатної або від’ємної) компоненти. Приклад такого
ряду демонструє рис. 9.1 в). Результат впливу випадкових чинників позначається
випадковою компонентою Еt,
яку обчислюють як залишок або похибку, що залишається після вилучення з
часового ряду систематичних компонент. Це не означає, що така складова не
підлягає подальшому аналізу, оскільки містить лише хаос.

Рисунок 9.1 – Головні компоненти
часового ряду:
а – тренд, що зростає; б – сезонна компонента; в – випадкова
компонента
Окремий
розрахунок компонент ![]() носить назву фільтрації компонент. Якщо необхідно розрахувати
значення тренду разом із сезонною складовою, тобто
носить назву фільтрації компонент. Якщо необхідно розрахувати
значення тренду разом із сезонною складовою, тобто ![]() , то дана процедура називається згладжуванням, а отриманий при цьому ряд – тренд-сезонним
часовим рядом.
, то дана процедура називається згладжуванням, а отриманий при цьому ряд – тренд-сезонним
часовим рядом.
Розглянемо приклад фільтрації компонент деякого умовного часового ряду,
зображеного на рисунку 9.2
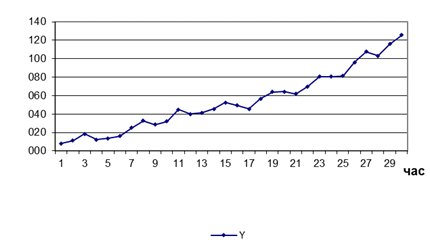
Рисунок 9.2
Нехай нам відомі
відфільтровані компоненти ряду, що графічно зображені на рисунках 9.3 а)-в)
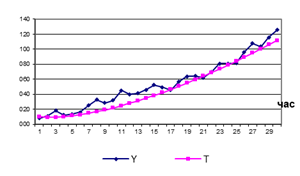
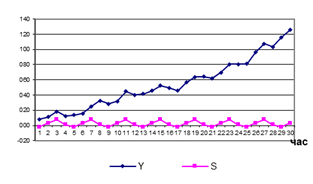
а) трендова
компонента U(t)=3t1,3–5t+12 б)
сезонна компонента
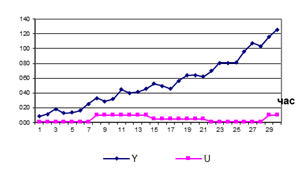
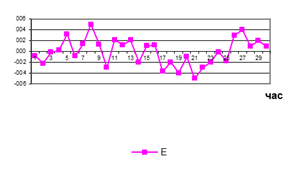
в) циклічна компонента г)
випадкова компонента
Рисунок 9.3
Спроба визначити тренд за вихідним часовим рядом, як видно з рисунку 9.4,
дала не зовсім адекватний результат, якщо порівняти рівняння тренду реального
та отриманого.
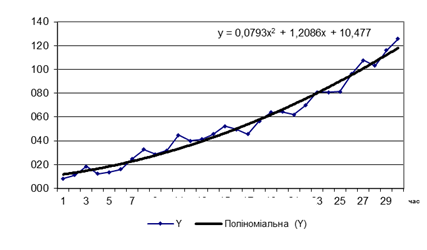
Рисунок 9.4
Тому проблема
адекватної декомпозиції часового ряду є достатньо серйозною.
Часовий ряд правильно
відображає об’єктивний закон зміни економічного показника, коли рівні цього
ряду є порівнянними, однорідними, сталими
та мають достатню сукупність спостережень. Невиконання однієї із цих умов
робить некоректним застосування математичного апарату для аналізу часового
ряду.
9.2 Ідентифікація часового ряду
Економетричне моделювання
відбувається, як правило, на підставі лише однієї реалізації випадкового
процесу, тож ясно, що про оцінювання сукупності всіх функцій розподілу взагалі
годі казати. Окрім того, якщо процес поводиться так, що його основні
статистичні характеристики з часом змінюються, то за короткий проміжок часу
спостережень про нього взагалі нічого не можна сказати. Проблема втрачає
гостроту, якщо розглядати вужчий клас випадкових процесів, який дістав назву стаціонарних випадкових процесів. Під стаціонарністю розуміють такі
випадкові процеси, деякі властивості яких не змінюються з часом.
Однією з важливіших
властивостей стаціонарного випадкового процесу є ергодичність. Вона полягає в тому, що кожна окрема реалізація
випадкового процесу є так би мовити «повноважним» представником усієї
сукупності можливих реалізацій. Звідси для ергодичних процесів основні
характеристики можна приблизно розраховувати не за кількома реалізаціями, як це
робиться в загальному випадку, а за будь-якою однією реалізацією за доволі
тривалий проміжок часу. В практичних розрахунках розглядають стаціонарний
процес у широкому сенсі.
Стаціонарний часовий ряд у широкому
сенсі – це
процес, для якого математичне сподівання та дисперсія існують і є сталими
величинами, що не змінюються в часі, а автокореляційна (автоковаріаційна)
функція залежить лише від різниці між двома моментами часу ![]() і не залежить від конкретного періоду часу.
Тобто для реалізації випадкового процесу
і не залежить від конкретного періоду часу.
Тобто для реалізації випадкового процесу ![]() основні моменти залишаються постійними й
обмеженими у разі зміні часу
основні моменти залишаються постійними й
обмеженими у разі зміні часу ![]() , для якого вони розраховуються, а
саме:
, для якого вони розраховуються, а
саме:
математичне сподівання: ![]() , для всіх
, для всіх ![]() ;
;
дисперсія: ![]() , для всіх
, для всіх ![]() ;
;
автоковаріація порядку![]() :
:
![]() ,
,
для всіх ![]() .
.
Структуру часового ряду в деяких випадках можна
визначити графічно. Це стосується, наприклад, таких компонент ряду, як тренд і
сезонні коливання. Однак чисту випадковість інколи помилково сприймають як
наявність певної структури, і, навпаки, за шумом можна не розгледіти існування
структури. Тому потрібні методи або інструменти, за допомогою яких можна було б
звести нанівець ефект впливу шуму, після чого з’ясувати характеристики ряду,
необхідні для побудови відповідної прогнозової моделі. Як правило, спочатку
з’ясовують, із яким процесом доведеться працювати – стаціонарним чи
нестаціонарним.
Реальні часові ряди в економіці, як правило, є динамічно
нестабільними, отже – не стаціонарними, і поняття стаціонарності процесу
часто є лише зручною абстракцією для застосування статистичних методів. Кожен
рівень часового ряду формується під впливом великої кількості чинників, які
відображають закономірність і випадковість його формування. В аналізі часових
рядів прийнято представляти часовий ряд ![]() у вигляді суми систематичної складової
(середньої) та випадкового відхилення від неї.
у вигляді суми систематичної складової
(середньої) та випадкового відхилення від неї.
Перевірку гіпотез стосовно сталості середнього значення
та дисперсії часового ряду можна здійснити кількома способами.
Найпростішими з них є
метод перевірки
різниць середніх рівнів і метод Форстера-Стьюарта.
Стаціонарні ряди ще називають динамічно стабільними або такими, що мають нульовий порядок
інтеграції ![]() .
.
Порядком інтеграції є число, що показує, скільки разів
часовий ряд потребує застосування оператора перших різниць, щоб стати
стаціонарним рядом.
Позначимо через ![]() порядок інтеграції.
Часовий ряд має одиничний корінь, або порядок інтеграції одиницю (
порядок інтеграції.
Часовий ряд має одиничний корінь, або порядок інтеграції одиницю (![]() ), якщо
), якщо ![]() є стаціонарним рядом, тобто ряд перших різниць
має нульовий порядок інтеграції (
є стаціонарним рядом, тобто ряд перших різниць
має нульовий порядок інтеграції (![]()
![]() ). Часовий ряд має два одиничні корені, або порядок
інтеграції 2, якщо його другі різниці є стаціонарним рядом:
). Часовий ряд має два одиничні корені, або порядок
інтеграції 2, якщо його другі різниці є стаціонарним рядом: ![]() ;
; ![]() . У загальному випадку
часовий ряд має порядок інтеграції
. У загальному випадку
часовий ряд має порядок інтеграції ![]() :
: ![]() , якщо
, якщо ![]() . Зазначимо: якщо ряд стаціонарний, то будь-які його різниці
залишаються стаціонарним рядом:
. Зазначимо: якщо ряд стаціонарний, то будь-які його різниці
залишаються стаціонарним рядом: ![]() тощо.
тощо.
За видом нестаціонарності часові ряди, що застосовують в
економічній практиці, розподіляють на ряди типу: TS, DS, тренд-сезонні,
нелінійні.
Часовий ряд типу TS (trend stationary process). До цього типу
відносять нестаціонарні часові ряди із детермінованим поліноміальним трендом ![]() , де
, де ![]() поліном ступеня
поліном ступеня ![]() від
від ![]() , а
, а ![]() – стаціонарний процес, який не обов’язково є білим шумом.
Нестаціонарний процес типу TS зводять до стаціонарного за допомогою кількох
методів. Наприклад, для лінійного тренду
– стаціонарний процес, який не обов’язково є білим шумом.
Нестаціонарний процес типу TS зводять до стаціонарного за допомогою кількох
методів. Наприклад, для лінійного тренду ![]() перехід до
стаціонарності може відбуватися:
перехід до
стаціонарності може відбуватися:
-
шляхом виділення
лінійного тренду. Наприклад, будують лінійну регресію за часом і розглядають
стаціонарний залишок ![]() ;
;
-
узяттям перших
різниць.
Часовий ряд типу DS (differencing stationary process). Це
ряди без періодичної складової та тенденції зростання, але наявність тренду в
дисперсії засвідчує їхню нестаціонарність. Прикладом таких рядів є процес
випадкового блукання ![]() . Як уже зазначалося, цей процес накопичує випадкові збурення
від усіх попередніх шоків, тобто має нескінченну пам’ять. Такий процес описують
стохастичним трендом і зводять до стаціонарного шляхом узяття першої різниці,
звідси й відповідна назва.
. Як уже зазначалося, цей процес накопичує випадкові збурення
від усіх попередніх шоків, тобто має нескінченну пам’ять. Такий процес описують
стохастичним трендом і зводять до стаціонарного шляхом узяття першої різниці,
звідси й відповідна назва.
Тренд-сезонні часові
ряди окрім тренду містять
чітко виражені сезонні коливання, які, своєю чергою, спричинюють
нестаціонарність. Якщо процес включає періодичні (сезонні) коливання навколо
середнього значення з періодом ![]() , тобто
, тобто ![]() із точністю до
випадкової складової, то d цьому разі
різниці через
із точністю до
випадкової складової, то d цьому разі
різниці через ![]() часових інтервалів
представляють стаціонарний процес
часових інтервалів
представляють стаціонарний процес
![]() ,
, ![]() де
де ![]() —
— ![]() ,
,
середнє значення якого збігається із середнім значенням
початкового ряду.
Нелінійні динамічні
процеси.
До цього типу відносять часові ряди зі складною структурою, вони мають тренд і
містять різні види коливань, зокрема сезонні та циклічні. Структуру таких рядів
узагалі не можна описати за допомогою відомих функцій, оскільки для різних
ділянок часового ряду набір цих функцій буде різним, тобто в цьому разі можна
говорити про ряди зі змінною структурою, які характерні для нелінійних
динамічних процесів. Вони спостерігаються в динаміці цін на ринках капіталу
тощо.
9.3 Дослідження
автокореляційної функції часового ряду (АКФ)
Властивістю автокореляційної функцій є те,
що для стаціонарних рядів існує таке значення К, що для ![]() коефіцієнти
автокореляції
коефіцієнти
автокореляції ![]() приймають майже нульові
значення. Отже, якщо зі збільшенням часового проміжку
приймають майже нульові
значення. Отже, якщо зі збільшенням часового проміжку ![]() АКФ ряду за абсолютним
значенням поступово згасає, ряд можна вважати стаціонарним. Якщо поведінка
автокореляційної функції не така, то вона не може бути автокореляційною функцією
стаціонарного процесу. На практиці порядок
АКФ ряду за абсолютним
значенням поступово згасає, ряд можна вважати стаціонарним. Якщо поведінка
автокореляційної функції не така, то вона не може бути автокореляційною функцією
стаціонарного процесу. На практиці порядок ![]() АКФ рекомендується
обирати від п/4 до п/3. Значення коефіцієнта автокореляції,
близьке до одиниці, вказує на значну додатну залежність між фактичним рядом
даних і рядом, зрушеним на
АКФ рекомендується
обирати від п/4 до п/3. Значення коефіцієнта автокореляції,
близьке до одиниці, вказує на значну додатну залежність між фактичним рядом
даних і рядом, зрушеним на ![]() одиниць часу. У
цьому разі пари спостережень будуть близькими один до одного. Якщо з’ясується,
що більше спостереження утворює пару з меншим, то коефіцієнт
автокореляції буде від’ємним і близьким до – 1. Для перевірки статистичної
значущості коефіцієнтів автокореляції не існує простих критеріїв.
одиниць часу. У
цьому разі пари спостережень будуть близькими один до одного. Якщо з’ясується,
що більше спостереження утворює пару з меншим, то коефіцієнт
автокореляції буде від’ємним і близьким до – 1. Для перевірки статистичної
значущості коефіцієнтів автокореляції не існує простих критеріїв.
Перевірка за критерієм
стандартної похибки коефіцієнта автокореляції. Якщо
обсяг вибірки (п) великий, окремі
(кожного порядку) коефіцієнти автокореляції випадкових даних мають вибірковий
розподіл, який наближається до нормального з нульовим математичним сподіванням
і середнім квадратичним відхиленням, що дорівнює
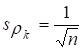 . (9.8),
. (9.8),
Якщо ![]() виходить за межі інтервалу
виходить за межі інтервалу 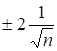 , то часовий ряд має
суттєву автокореляцію
, то часовий ряд має
суттєву автокореляцію ![]() -го порядку. Зазначимо: якщо обчислено 20 значень
АКФ, то на 5-відсотковому рівні значущості в середньому один із 20 буде
значущим. Цей факт разом із відносно малим обсягом вибірки на практиці означає,
що критерій на підставі окремих коефіцієнтів може бути ненадійним.
Альтернативою є використання критерію Бокса-Пірса.
-го порядку. Зазначимо: якщо обчислено 20 значень
АКФ, то на 5-відсотковому рівні значущості в середньому один із 20 буде
значущим. Цей факт разом із відносно малим обсягом вибірки на практиці означає,
що критерій на підставі окремих коефіцієнтів може бути ненадійним.
Альтернативою є використання критерію Бокса-Пірса.
Q – критерій Бокса-Пірса використовують для перевірки
значущості всієї множини коефіцієнтів автокореляції як групи. Статистичний Q-критерій обчислюють за формулою:
![]() , (9.10)
, (9.10)
де ![]() – оцінка автокореляції порядку
– оцінка автокореляції порядку ![]() ;
;
т – найбільший лаг, що розглядається.
Якщо всі автокореляції до порядку т дорівнюють нулю, то Q має приблизно ![]() -розподіл із т
ступенів свободи. Велике значення Q порівняно
з критичним зумовлює відхилення нульової гіпотези.
-розподіл із т
ступенів свободи. Велике значення Q порівняно
з критичним зумовлює відхилення нульової гіпотези.
Визначити, які невипадкові чинники, окрім
випадкових, беруть участь у формуванні значень часового ряду, можна за
допомогою автокореляційного аналізу. Сутність методу полягає в застосуванні
апарату перших різниць і аналізу автокореляцій для ідентифікації часових рядів
таких видів:
1)
ряд не має тренду, якщо коефіцієнти автокореляції між рівнями ряду не залежать
від часового лагу (статистично незначущі) і не мають певної закономірності
зміни;
2)
ряд має лінійний адитивний тренд у разі,
коли автокореляційний аналіз вказує на лінійну залежність зміни коефіцієнтів
автокореляції від часового лагу, а перехід до перших різниць виключає цю
залежність;
3)
ряд містить сезонну складову, якщо не існує лінійної залежності зміни
коефіцієнтів автокореляції від часового лагу, але корелограма містить велику кількість значущих максимальних і мінімальних
значень коефіцієнтів автокореляцій, що свідчить про значну залежність між
спостереженнями, зрушеними на однаковий часовий інтервал;
4)
ряд має лінійний тренд і сезонну складову,
якщо його корелограма вказує на лінійну залежність зміни коефіцієнтів автокореляції від часового лагу і містить велику
кількість значущих максимальних і мінімальних значень коефіцієнтів
автокореляцій, а перехід до перших різниць виключає лінійний тренд, але
статистична значущість певних коефіцієнтів автокореляцій залишається.
9.4 Методи
фільтрації сезонної компоненти
Проблема аналізу сезонності (та/або циклічності)
полягає у дослідженні сезонних коливань і у вивченні зовнішнього циклічного
механізму, що їх породжує. Для дослідження суто сезонних коливань необхідно
виокремити з часового ряду уt
сезонну компоненту st і
потім аналізувати її динаміку. Більшість методів фільтрації побудовано таким
чином, що попередньо виокремлюється тренд, а потім сезонна компонента. Тренд у
чистому вигляді необхідний і для аналізу динаміки сезонної хвилі. Оскільки
індекси сезонності сезонної хвилі величини безрозмірні і не змінюються з року в
рік, то їх можна використовувати для визначення рівня сезонності у часовому
ряду. У разі використання квартальних даних їх буде чотири, а місячних
спостережень – 12.
Найпростішим
способом, який характеризує коливання рівнів досліджуваного показника, є
розрахунок питомої ваги кожного рівня в загальному річному обсязі, або індексу
сезонності.
Часові ряди з
інтервалом менше року (місяць, квартал), як правило, містять сезонність.
Сезонна компонента ![]() має період m:
має період m: ![]() (m = 12 для ряду місячних даних; m = 4 –
для ряду квартальних даних). Окрім того, відомо, що m кратне n, тобто
(m = 12 для ряду місячних даних; m = 4 –
для ряду квартальних даних). Окрім того, відомо, що m кратне n, тобто ![]() , k – ціле
число. Очевидно, якщо m – кількість
місяців або кварталів у році, то k –
кількість років, представлених у часовому ряду {уt}. Тому
вхідні дані тренд-сезонного часового ряду часто представляють у вигляді матриці
{yij} розміру [k х m].
, k – ціле
число. Очевидно, якщо m – кількість
місяців або кварталів у році, то k –
кількість років, представлених у часовому ряду {уt}. Тому
вхідні дані тренд-сезонного часового ряду часто представляють у вигляді матриці
{yij} розміру [k х m].
Розглянемо таку
модель:
![]() , (9.11)
, (9.11)
де ![]() – «річна» складова (тренд);
– «річна» складова (тренд);
![]() – індекс сезонності, або стала
пропорційності для j-го кварталу
(місяця), яка є безрозмірною величиною та не змінюється з року в рік.
– індекс сезонності, або стала
пропорційності для j-го кварталу
(місяця), яка є безрозмірною величиною та не змінюється з року в рік.
Індекс сезонності Іj характеризує
ступінь відхилення рівня сезонного часового ряду від ряду середніх ![]() (тренду) або, інакше кажучи, ступінь коливань
відносно 100 %. Наближені оцінки індексів обчислюють як:
(тренду) або, інакше кажучи, ступінь коливань
відносно 100 %. Наближені оцінки індексів обчислюють як:
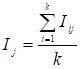 або
або 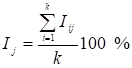 , (9.12)
, (9.12)
де
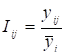 та
та 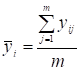 . (9.13)
. (9.13)
Якщо відомі оцінки тренду ![]() і
сезонної компоненти
і
сезонної компоненти ![]() в
адитивній моделі, то
в
адитивній моделі, то ![]() можна
оцінити точніше:
можна
оцінити точніше:
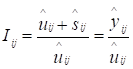 . (9.14)
. (9.14)
Останнє
свідчить про можливості оцінювання рівня сезонності незалежно від того, яку
модель розглядають: адитивну або мультиплікативну. Недоліком цього підходу є
те, що він не враховує наявності випадкових коливань і тенденцію зміни
середньорічного рівня й сезонної хвилі.
9.5 Прогнозування
тенденції часового ряду
Механічні методи згладжування часових рядів використовують фактичні значення
сусідніх рівнів ряду і не досліджують аналітичний вид згладженої функції. Вони мають
механізм автоматичного налагодження на зміну досліджуваного показника. Завдяки
цьому модель постійно пристосовується до зміни інформації й наприкінці
інтервалу прогнозової бази відображає тенденцію, що склалася на поточний
момент. До механічних методів
належать: згладжування по двох точках, метод простої ковзкої середньої, метод
зваженої ковзкої середньої, метод експоненційного згладжування.
Аналітичні методи згладжування часових рядів ґрунтуються на припущенні, що
відомий загальний вигляд невипадкової складової часового ряду. Вони
реалізуються за допомогою регресійних та адаптивних методів.
Регресійні методи є основою побудови кривих
зростання. Для відображення економічних процесів існує велика кількість видів
кривих зростання. Щоб правильно підібрати найдоцільнішу криву для моделювання й
прогнозування економічного явища, необхідно знати особливості кожного виду
кривих.
Вибір форми
кривої для згладжування певною мірою залежить від мети згладжування:
інтерполяції або екстраполяції. У першому випадку метою є досягнення
найбільшої близькості до фактичних рівнів часового ряду. У другому –
виявлення основної закономірності розвитку явища, стосовно якої можна
припустити, що в майбутньому вона збережеться.
На практиці під час попереднього аналізу
часового ряду обирають, як правило, дві-три криві зростання для подальшого
дослідження і побудови трендової моделі часового ряду.
Адаптивні методи
прогнозування застосовуються в ситуації зміни зовнішніх умов, коли найбільш важливими
стають останні реалізації досліджуваного процесу. Загальна схема побудови
адаптивних методів може бути подана так:
1) за кількома першими рівнями ряду
будується модель і оцінюються її параметри;
2) на основі побудованої моделі
розраховується прогноз на один крок вперед, причому його відхилення від
фактичного рівня ряду розцінюється як помилка прогнозування, яка враховується
відповідно до прийнятої схеми коригування моделі;
3) за моделлю з відкоригованими
параметрами розраховується прогнозна оцінка на наступний момент часу тощо.
Схему такого процесу представлено на
рис. 5.3.
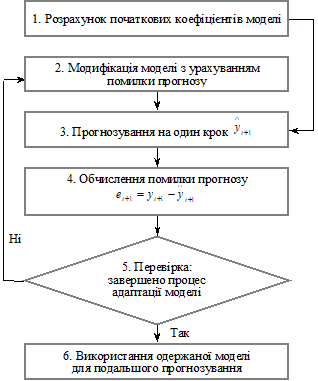
Рисунок
9.5 – Схема побудови адаптивних моделей
Після надходження фактичного значення
обчислюється помилка, розбіжність між фактичним і прогнозованим рівнем
(довготермінова функція моделі): ![]() .
.
У моделі передбачається, що зміна фактичного
рівня є деякою часткою (![]() ) від очікуваної зміни
) від очікуваної зміни ![]() . Параметр
. Параметр ![]() називається
коригувальним коефіцієнтом або параметром адаптації. За критерій оптимальності
під час вибору параметра адаптації можна взяти мінімум середнього квадрата
помилок прогнозування. Чим ближчий
називається
коригувальним коефіцієнтом або параметром адаптації. За критерій оптимальності
під час вибору параметра адаптації можна взяти мінімум середнього квадрата
помилок прогнозування. Чим ближчий ![]() до одиниці, тим більше
сподівання економічних суб’єктів відповідають реальній динаміці часового ряду,
і навпаки, чим ближче до нуля – тим менше володіємо ситуацією, тому треба
вносити корективи.
до одиниці, тим більше
сподівання економічних суб’єктів відповідають реальній динаміці часового ряду,
і навпаки, чим ближче до нуля – тим менше володіємо ситуацією, тому треба
вносити корективи.
Таким чином, модель постійно вбирає в себе
нову інформацію і до кінця періоду навчання відбиває тенденцію розвитку
процесу, що існує на даний момент. Прогноз отримується як екстраполяція
останньої тенденції. Численні адаптивні методи відрізняються один від одного
лише способами числової оцінки параметрів моделі і визначення параметрів
адаптації. Базовими адаптивними методами вважаються методи Хольта, Брауна і
Хольта-Уїнтерса.
Модель Брауна
Якщо є часовий ряд спостережень ![]() , то прогноз в момент часу t на
, то прогноз в момент часу t на ![]() кроків вперед можна
здійснити за формулою
кроків вперед можна
здійснити за формулою
![]() (9.15)
(9.15)
де ![]() – поточні оцінки коефіцієнтів адаптивного поліному.
– поточні оцінки коефіцієнтів адаптивного поліному.
В моделі Брауна модифікація (адаптація)
коефіцієнтів лінійної моделі здійснюється наступним чином
![]() ,
, ![]() (9.16)
(9.16)
де ![]() – коефіцієнт дисконтування даних,
– коефіцієнт дисконтування даних,
![]() – похибка прогнозу (
– похибка прогнозу (![]() ).
).
Початкові значення параметрів моделі можна
визначити за методом МНК на основі декількох перших спостережень. Оптимальне значення
параметра дисконтування знаходиться в межах [0;1], визначається методом
чисельної оптимізації і є постійним для всього періоду спостережень. За рахунок
оператору В можна зрушувати всю послідовність на один крок назад: ![]() . Застосування оператору В до спостережень і до коефіцієнтів
адаптивного поліному дозволяє виразити модель Брауна у вигляді
. Застосування оператору В до спостережень і до коефіцієнтів
адаптивного поліному дозволяє виразити модель Брауна у вигляді
![]() . (9.17)
. (9.17)
Тоді модель Брауна можна трактувати як модель
авторегресії ARIMA
(0, 2, 2)-моделлю: ![]() з коефіцієнтами
ковзної середньої –
з коефіцієнтами
ковзної середньої – ![]() та
та ![]() .
.
Точковий прогноз розраховують після
підстановки значення ![]() в оцінювану модель.
Межі інтервалу надійності прогнозу можна визначити за формулою:
в оцінювану модель.
Межі інтервалу надійності прогнозу можна визначити за формулою:
![]() , (9.18)
, (9.18)
де величини ![]() .
.