ЛАБОРАТОРНА РОБОТА
№ 1
Тема: ПРОВЕДЕННЯ КОРЕЛЯЦІЙНОГО
АНАЛІЗУ
Мета роботи: здійснити кореляційний аналіз статистичної сукупності
спостережень факторів.
Зміст роботи: виявлення взаємозв’язку між випадковими змінними шляхом точкової
оцінки парних (частинних) коефіцієнтів кореляції, розрахунку та перевірки
значущості множинних коефіцієнтів кореляції та детермінації. На основі
проведеного аналізу здійснення відбору факторів, що виробляють найбільший вплив
на результуючий показник, та дослідження наявності мультиколінеарності.
Вимоги до звіту: назва, тема,
мета, завдання, розрахункові формули. Результати аналітичного розв’язання
задачі та комп’ютерного у вигляді таблиці MS Excel з вихідними умовами експерименту,
таблиці MS Excel з результатами обчислень, висновок про отримані результати.
Опис інструментів та функцій MS Excel, що використовувались при вирішенні
задачі. Короткий опис технології вирішення задачі в MS Excel.
1.
Знайдемо парні коефіцієнти кореляції
між залежною (Y) та незалежними (X1, X2, X3) змінними.
Нехай задано дві вибірки (обов’язково з однаковою кількістю даних,
в нашому випадку n = 20), що відображають дві випадкові величини Х1, Y:

Коефіцієнт парної кореляції визначають як коваріацію, нормовану за
стандартними відхиленнями випадкових величин
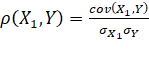 ,
, 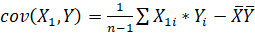 ,
(1)
,
(1)
де ![]() – середньоквадратичне
відхилення незалежної змінної,
– середньоквадратичне
відхилення незалежної змінної,
![]() – середньоквадратичне
відхилення залежної змінної.
– середньоквадратичне
відхилення залежної змінної.

Середньоквадратичне відхилення — дорівнює кореню квадратному з дисперсії випадкової величини:
![]()
Відповідно до формул з обчислення дисперсії:
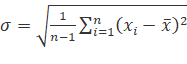 , (2)
, (2)
У комірках L7 та L8 записуються формули ![]() і
і ![]() для розрахунку
середньоквадратичних відхилень залежної та незалежної змінної.
для розрахунку
середньоквадратичних відхилень залежної та незалежної змінної.
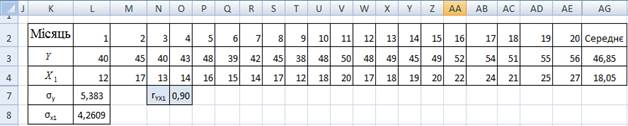
Коефіцієнт парної кореляції визначають за
формулою ![]() , що записується в комірці О7.
, що записується в комірці О7.
2. Коефіцієнт кореляції набуває значення від
–1 до +1.
Якщо |r|<0,30, то зв’язок між ознаками слабкий;
0,30≤|r|≤0,70
– помірний зв’язок;
|r|>0,70 –
сильний або щільний зв’язок.
Коли |r|=1 – зв’язок функціональний.
Якщо |r|≈0, то лінійний зв’язок між Х та У
відсутній. Але можливе нелінійна взаємодія, а це потребує додаткової перевірки.
За таким принципом розраховуються коефіцієнти
парної кореляції для пар:Y-X1, Y-X2, Y-X3.
2.1.
Знайдемо коефіцієнти кореляції між
пояснюючими змінними.
Обчислимо середні значення та стандартні відхилення пояснюючих змінних ![]() . Для цього можна скористатись стандартними функціями MS Excel.
В майстрі функцій знайдемо категорію «статистичні» і в ній функції «СРЗНАЧ» та «СТАНДОТКЛ».
. Для цього можна скористатись стандартними функціями MS Excel.
В майстрі функцій знайдемо категорію «статистичні» і в ній функції «СРЗНАЧ» та «СТАНДОТКЛ».
Дані величини можна також розрахувати за формулами:
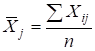 ,
(3)
,
(3)
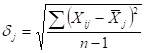 , (4)
, (4)
де ![]() середнє значення
середнє значення ![]() -тої пояснюючої змінної;
-тої пояснюючої змінної;
![]() індивідуальне значення
індивідуальне значення ![]() -тої пояснюючої змінної;
-тої пояснюючої змінної;
![]() – номер пояснюючої
змінної;
– номер пояснюючої
змінної;
![]() – номер точки
спостереження (місяця);
– номер точки
спостереження (місяця);
![]() стандартне відхилення
стандартне відхилення ![]() -тої пояснюючої змінної;
-тої пояснюючої змінної;
![]() – число спостережень.
– число спостережень.
Додаткові розрахунки наведено в табл.1.
Таблиця 1 – Проміжні розрахунки
|
Місяць |
|
|
|
|
|
|
|
|
1 |
40 |
12 |
5 |
15 |
36,60 |
21,16 |
23,04 |
|
2 |
45 |
17 |
7 |
18 |
1,10 |
6,76 |
3,24 |
|
3 |
40 |
13 |
6 |
16 |
25,50 |
12,96 |
14,44 |
|
4 |
43 |
14 |
7 |
17 |
16,40 |
6,76 |
7.84 |
|
5 |
48 |
16 |
6 |
20 |
4,20 |
12,96 |
0,04 |
|
6 |
39 |
15 |
5 |
15 |
9,30 |
21,16 |
23,04 |
|
7 |
42 |
14 |
6 |
16 |
16,40 |
12,96 |
14,44 |
|
8 |
45 |
17 |
9 |
18 |
1,10 |
0,36 |
3,24 |
|
9 |
38 |
12 |
5 |
19 |
36,60 |
21,16 |
0,64 |
|
10 |
48 |
18 |
10 |
20 |
0,00 |
0,16 |
0,04 |
|
11 |
50 |
20 |
11 |
22 |
3,80 |
1,96 |
4,84 |
|
12 |
48 |
17 |
10 |
21 |
1,10 |
0,16 |
1,44 |
|
13 |
49 |
18 |
12 |
21 |
0,00 |
5,76 |
1,44 |
|
14 |
45 |
19 |
8 |
20 |
0,90 |
2,56 |
0,04 |
|
15 |
49 |
20 |
9 |
22 |
3,80 |
0,36 |
4,84 |
|
16 |
52 |
22 |
14 |
23 |
15,60 |
19,36 |
10,24 |
|
17 |
54 |
24 |
15 |
24 |
35,40 |
29,16 |
17,64 |
|
18 |
51 |
21 |
13 |
20 |
8,70 |
11,56 |
0,04 |
|
19 |
55 |
25 |
16 |
24 |
48,30 |
40,96 |
17,64 |
|
20 |
56 |
27 |
18 |
25 |
80,10 |
70,56 |
27,04 |
|
Всього |
937 |
361 |
192 |
396 |
344,95 |
298,80 |
175,21 |
![]() ;
; ![]() ;
; ![]() .
.
![]() ;
; ![]() ;
; ![]() .
.
Нормалізуємо пояснюючі змінні. Серед статистичних функцій MS Excel
знайдемо функцію «НОРМАЛІЗАЦІЯ» та нормалізуємо ![]() .
.
Для цього у комірки F3, G3, H3 запишемо формули нормалізації:
![]()
![]()
![]() та за допомогою маркера
заповнення скопіюємо їх у діапазон F3: H22. Отримаємо наступний результат:
та за допомогою маркера
заповнення скопіюємо їх у діапазон F3: H22. Отримаємо наступний результат:
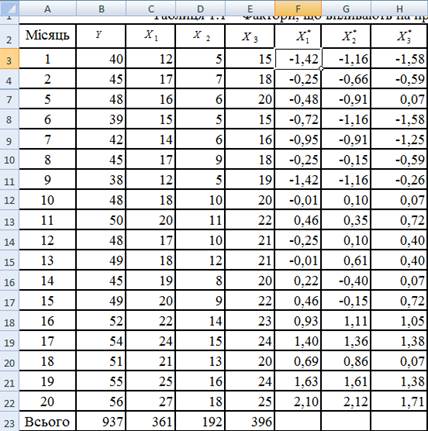
Для цього можна також скористатись формулою:
![]()
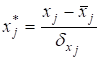 (5)
(5)
|
|
|
|
|
|
-1,4199 |
-1,1600 |
-1,5807 |
|
|
-0,2464 |
-0,6556 |
-0,5928 |
|
|
-1,1852 |
-0,9078 |
-1,2514 |
|
|
-0,9505 |
-0,6556 |
0,9221 |
|
|
-0,4811 |
-0,9078 |
0,0660 |
|
|
-0,7158 |
-1,1600 |
-1,5807 |
|
|
-0,9505 |
-0,9078 |
-1,2514 |
|
|
-0,2464 |
-0,1513 |
-0,5928 |
|
|
-1,4199 |
-1,1600 |
-0,2635 |
|
|
-0,0117 |
0,1009 |
0,0659 |
|
|
0,4577 |
0,3530 |
0,7245 |
|
|
-0,2464 |
0,1009 |
0,3952 |
|
|
-0,0117 |
0,6052 |
0,3952 |
|
|
0,2230 |
-0,4035 |
0,0659 |
|
|
0,4577 |
-0,1513 |
0,7245 |
|
|
0,9270 |
1,1095 |
1,0538 |
|
|
1,3964 |
1,3617 |
1,3831 |
|
|
0,6923 |
0,8574 |
0,0659 |
|
|
1,6311 |
1,6139 |
1,3831 |
|
|
2,1005 |
2,1182 |
1,7124 |
Транспонуємо матрицю ![]() (нормалізовану) в матрицю
(нормалізовану) в матрицю ![]()
Для транспонування
матриці використовуємо стандартну функцію MS Excel «ТРАНСП». Для використання даної функції слід виконати наступні кроки:
Крок 1: У комірку B25 формулу: ![]() .
.
Крок 2: Виділити весь діапазон, де буде
розміщена транспонована матриця: B25:U27.
Крок 3: Натиснути функціональну клавішу F2, а потім клавіші Ctrl+Shift+Enter. В результаті отримаємо
транспоновану матрицю ![]() :
:

2.2.
Перемножимо матриці ![]() та
та ![]() .
.
Для множення матриць використовується функцію MS Excel «МУМНОЖ». Для використання даної функції слід виконати наступні кроки:
Крок 1: Виділити комірку, яка буде лівим
верхнім кутом результуючої матриці, наприклад В29.
Крок 2: У виділену комірку записати формулу: ![]() , де першим аргументом є діапазон транспонованої нормалізованої матриці
, де першим аргументом є діапазон транспонованої нормалізованої матриці ![]() , а другим – вихідної нормалізованої матриці
, а другим – вихідної нормалізованої матриці ![]() .
.
Крок 3: Виділити весь діапазон, де буде
розміщений результат множення матриць (В29:D31).
Крок 4: Натиснути функціональну клавішу F2, а потім клавіші Ctrl+Shift+Enter. В результаті отримаємо перемножені матриці ![]()
![]() .
.
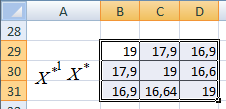
2.3. Знайдемо кореляційну матрицю ![]()
![]() .
.
Для знаходження кореляційної матриці ![]() необхідно кожний
елемент матриці
необхідно кожний
елемент матриці ![]()
![]() помножити на
помножити на ![]() (у нашому випадку
(у нашому випадку ![]() ):
):
|
|
1 |
0,9419 |
0,8914 |
|
0,9419 |
1 |
0,8759 |
|
|
0,8917 |
0,8759 |
1 |
Визначити значущі коефіцієнти кореляції, використовуючи розподіл
Фішера-Іейтса.
Отже, якщо виявиться, що знайдений за вибіркою коефіцієнт r задовольняє
нерівності
![]()
то його потрібно визнати значущим.
4. Знайдемо визначник матриці ![]()
![]()
![]() .
.
Для знаходження ![]()
![]() необхідно серед
математичних функцій MS Excel знайти функцію «МОПРЕД». Так як кореляційна матриця
знаходиться в комірках діапазону G29:I31, тоді для встановлення визначника слід задати формулу:
необхідно серед
математичних функцій MS Excel знайти функцію «МОПРЕД». Так як кореляційна матриця
знаходиться в комірках діапазону G29:I31, тоді для встановлення визначника слід задати формулу: ![]() . Скориставшись нею, дістанемо:
. Скориставшись нею, дістанемо: ![]()
![]() = 0,0218.
= 0,0218.
Оскільки ![]()
![]() наближається до нуля,
то в масиві пояснюючих змінних може існувати мультиколінеарність.
наближається до нуля,
то в масиві пояснюючих змінних може існувати мультиколінеарність.
Прологарифмуємо визначник матриці ![]() :
: ![]()
![]()
![]() = -3,8249
= -3,8249
5. Обчислимо критерій Пірсона ![]() за формулою:
за формулою:
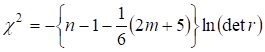 ,
(6)
,
(6)
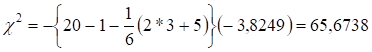 .
.
Знайдене значення ![]() порівняємо з табличним
значенням
порівняємо з табличним
значенням ![]() , коли маємо
, коли маємо ![]() ступенів свободи та
при рівні значущості
ступенів свободи та
при рівні значущості ![]() .
.
Оскільки ![]() , то в масиві пояснюючих змінних (продуктивність праці,
питомі інвестиції та фондовіддача) існує мультиколінеарність.
, то в масиві пояснюючих змінних (продуктивність праці,
питомі інвестиції та фондовіддача) існує мультиколінеарність.
6. Обчислимо ![]() критерій.
критерій.
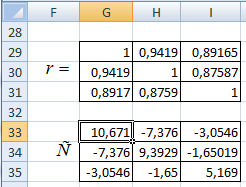
Для визначення ![]() критеріїв необхідно знайти матрицю
критеріїв необхідно знайти матрицю ![]() , яка є оберненою до матриці
, яка є оберненою до матриці ![]() .
.
Для знаходження оберненої матриці використовується функція MS Excel «МОБР». Для використання даної
функції слід виконати наступні кроки:
Крок 1: Виділити комірку, яка буде лівим
верхнім кутом результуючої матриці, наприклад G33.
Крок 2: У виділену комірку записати формулу: ![]() , де аргументами є діапазон кореляційної матриці
, де аргументами є діапазон кореляційної матриці ![]() .
.
Крок 3: Виділити весь діапазон, де буде
розміщена обернена матриці (G33:І35).
Крок 4: Натиснути функціональну клавішу F2, а потім клавіші Ctrl+Shift+Enter. В результаті отримаємо обернену матрицю ![]() :
:
Безпосередньо ![]() критерій обчислюється за формулою:
критерій обчислюється за формулою:
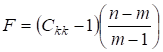 , (7)
, (7)
де ![]() – діагональний елемент
матриці
– діагональний елемент
матриці ![]() .
.
 ;
;
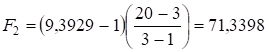 ;
;
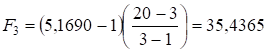 .
.
Обчислені критерії порівнюються з табличним значенням ![]() , коли є
, коли є ![]() ступенів свободи та
при рівні значущості
ступенів свободи та
при рівні значущості ![]() .
.
У розглядуваному випадку ![]() ,
, ![]() ,
, ![]() . Це означає, що кожна з пояснюючих змінних мультиколінеарна
з іншими.
. Це означає, що кожна з пояснюючих змінних мультиколінеарна
з іншими.
7. Визначимо частинні коефіцієнти кореляції ![]() .
.
Частинні коефіцієнти кореляції показують тісноту зв’язку між двома пояснюючими
змінними за умови, що всі інші змінні не впливають на цей зв’язок і
обчислюються за формулою:
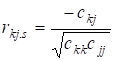 .
(8)
.
(8)
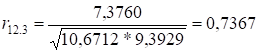 ;
;
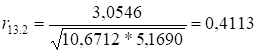 ;
;
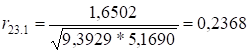 .
.
Отже, спираючись на здобуті нами значення окремих (частинних)
коефіцієнтів кореляції, можна сказати, що зв’язок між фондовіддачею та
продуктивністю праці є тісним, якщо не враховувати вплив питомих інвестицій,
зв’язок між фондовіддачею та питомими інвестиціями є слабким, якщо не брати до
уваги вплив продуктивності праці. Зв’язок між продуктивністю праці та питомими
інвестиціями також є слабким, якщо не враховувати фондовіддачу.
8. Визначимо ![]() критерій.
критерій.
Ці критерії застосовуються для визначення мультиколінеарності двох
пояснюючих змінних і обчислюються за формулою:
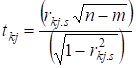 . (9)
. (9)
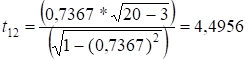 ;
;
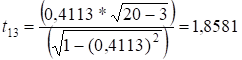 ;
;
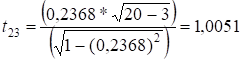 .
.
Обчислені ![]() критерії порівнюються з табличним значенням
критерії порівнюються з табличним значенням ![]() , коли маємо
, коли маємо ![]() ступенів свободи та
при рівні значущості
ступенів свободи та
при рівні значущості ![]() .
.
Оскільки ![]() , то продуктивність праці та фондовіддача є відповідно
мультиколінеарними між собою;
, то продуктивність праці та фондовіддача є відповідно
мультиколінеарними між собою;
![]() , тому відповідно продуктивність праці та питомі інвестиції є
мультиколінеарними між собою;
, тому відповідно продуктивність праці та питомі інвестиції є
мультиколінеарними між собою;
![]() , тому продуктивність праці та питомі інвестиції не є
мультиколінеарними між собою.
, тому продуктивність праці та питомі інвестиції не є
мультиколінеарними між собою.
9. Визначити залежність оцінок
параметрів економетричної моделі і коефіцієнтів парної кореляції за алгоритмом
покрокової регресії (на оцінку «відмінно»).
Висновок. Дослідження, проведені за
алгоритмом Фаррара-Глобера показали, що мультиколінеарність між пояснюючими
змінними даного прикладу існує. Отже, для того, щоб можна було застосувати
метод 1МНК для оцінювання параметрів моделі за цією інформацію, необхідно в
першу чергу звільнитися від мультиколінеарності.
1.
Знайти парні коефіцієнти кореляції між залежною та незалежними змінними.
2.
Визначити, який з факторів значно впливає на результуючий показник, а
який не значимо.
3.
Визначити множинний коефіцієнт кореляції результуючого показника з
пояснюючими, коефіцієнт детермінації та оцінити їх значущість.
4.
Дослідити наявність мультиколінеарності між пояснюючими змінними,
скориставшись алгоритмом Фаррара-Глобера.
5.
Додатково здійснити розрахунки по знаходженню кореляційної матриці за
допомогою MS Excel.
6.
Зробити висновки щодо взаємозв’язку статистичної сукупності спостережень
факторів та обґрунтувати відбір факторів, що в наступному можуть бути включені
до регресійного рівняння.
7.
Додатково здійснити розрахунки коефіцієнтів кореляції за допомогою
спеціалізованого інструментарію MS Excel (надбудова «Аналіз даних», функції
КОРРЕЛ(), СТЬЮДРАСПОБР(), FРАСПРОБР()).
8.
Визначити залежність оцінок параметрів економетричної моделі і
коефіцієнтів парної кореляції за алгоритмом покрокової регресії (на оцінку «відмінно»).
Початкові дані:
Для дослідження мультиколінеарності наведено статистичну сукупність
спостережень факторів, що впливають на прибуток підприємства (табл. 1.1).
Номери N1, N2, N3, N4 вибираються з таблиці 1.2.
Таблиця 1.1 – Фактори, що впливають на прибуток підприємства
|
Місяць |
Прибуток на місяць, грн., |
Фондовіддача, грн., |
Продуктивність праці, грн., |
Питомі інвестиції, грн., |
|
1 |
70-3*N4 |
32-2*N4 |
5+N4 |
25-N2 |
|
2 |
75-3*N3 |
37-2*N4 |
7+N1 |
28-N4 |
|
3 |
70-3*N1 |
33-2*N2 |
6+N3 |
26-N4 |
|
4 |
73-3*N2 |
34-2*N1 |
7+N1 |
27-N2 |
|
5 |
78-3*N4 |
36-2*N2 |
6+N4 |
30-N2 |
|
6 |
69-3*N4 |
35-2*N3 |
5+N1 |
25-N1 |
|
7 |
72-3*N1 |
34-2*N4 |
6+N3 |
26-N1 |
|
8 |
75-3*N2 |
37-2*N3 |
9+N2 |
28-N2 |
|
9 |
68-3*N1 |
32-2*N1 |
5+N3 |
29-N4 |
|
10 |
78-3*N2 |
38-2*N1 |
10+N3 |
30-N2 |
|
11 |
80-3*N4 |
40-2*N1 |
11+N2 |
32-N1 |
|
12 |
78-3*N3 |
37-2*N4 |
10+N4 |
31-N2 |
|
13 |
79-3*N1 |
38-2*N4 |
12+N4 |
31-N3 |
|
14 |
75-3*N4 |
39-2*N1 |
8+N1 |
30-N4 |
|
15 |
79-3*N2 |
40-2*N2 |
9+N4 |
32-N1 |
|
16 |
82-3*N1 |
42-2*N2 |
14+N4 |
33-N2 |
|
17 |
84-3*N4 |
44-2*N3 |
15+N2 |
34-N4 |
|
18 |
81-3*N2 |
41-2*N4 |
13+N4 |
30-N3 |
|
19 |
85-3*N3 |
45-2*N4 |
16+N3 |
34-N1 |
|
20 |
86-3*N2 |
47-2*N1 |
18+N1 |
35-N4 |
Таблиця 1.2 – Варіанти завдань
|
Варіант |
N1 |
N2 |
N3 |
N4 |
|
1 |
7 |
6 |
1 |
7 |
|
2 |
7 |
7 |
2 |
2 |
|
3 |
2 |
6 |
8 |
6 |
|
4 |
7 |
6 |
4 |
7 |
|
5 |
4 |
8 |
3 |
4 |
|
6 |
3 |
2 |
6 |
8 |
|
7 |
3 |
3 |
3 |
7 |
|
8 |
4 |
5 |
6 |
5 |
|
9 |
7 |
4 |
2 |
9 |
|
10 |
8 |
8 |
1 |
8 |
|
11 |
7 |
3 |
6 |
3 |
|
12 |
4 |
3 |
7 |
7 |
|
13 |
3 |
6 |
6 |
4 |
|
14 |
4 |
8 |
5 |
3 |
|
15 |
3 |
3 |
4 |
2 |
|
16 |
5 |
6 |
8 |
1 |
|
17 |
8 |
5 |
7 |
8 |
КОНТРОЛЬНІ ПИТАННЯ
1. Які задачі вирішує кореляційний аналіз?
2. Чим відрізняються коваріація та коефіцієнт кореляції?
3. Чим відрізняються і яким чином розраховуються коефіцієнти парної та
часткової кореляції?
4. Що показує вибірковий коефіцієнт множинної кореляції?
5. Яким чином пов’язані вибірковий та генеральний коефіцієнт кореляції?
6. Запишіть співвідношення між коефіцієнтами кореляції і детермінації.
7. Як визначаються дисперсія залишків, загальна дисперсія і дисперсія
регресії? Який між ними зв’язок?
8. Що показує і з якою метою вимірюється стандартна похибка величини?
9. Яким чином оцінюється значимість коефіцієнтів кореляції?
10. Що таке мультиколінеарність і які її наслідки?
11. Охарактеризуйте основні методи усунення мультиколінеарності.
12. В чому полягає суть алгоритма Фаррара-Глобера, що використовується для
виявлення мультиколінеарності?
13. Яким чином оцінюється тіснота нелінійного зв’язку?
14. Охарактеризуйте стисло алгоритм покрокової регресії.
15. Який інструментарій надає MS Excel для проведення кореляційного аналізу?