Тема: Побудова лінійної
багатофакторної моделі з
урахуванням мультиколінеарності.
Мета заняття: Задана вибірка, отримана для факторів X1, X2,
X3 і показника Y. Необхідно:
ü перевірити систему факторів на мультиколінеарність;
ü визначити оцінки
параметрів лінійної моделі Y =a0+a1 X1+a2, X2+a3 X3;
ü оцінити її
адекватність експериментальним даним з точністю Р=0,95.
Хід роботи
1.
Завантажити програму EXCEL.
2.
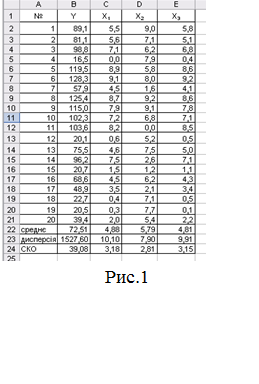
Сформувати таблицю вихідних даних, заповнивши діапазон
комірок А2:E21 (рис. 1).
3.
Виконати розрахунки:
3.1. Розрахуємо середнє значення факторів X1, X2, X3 і показника Y, використовуючи вбудовану
функцію СРЗНАЧ;
3.2. Розрахуємо вибіркові дисперсії величин факторів X1, X2, X3 і показника Y, використовуючи вбудовану
функцію ДИСП;
3.3 Розрахуємо середнє квадратичне відхилення (СКВ) факторів X, Y, Z і показника F, як корінь квадратний з
дисперсій відповідних величин, використовуючи вбудовану функцію КОРЕНЬ (рис.1).

4. Обчислимо
вибіркові парні коефіцієнти кореляції використовуючи вбудовану
функцію КОРРЕЛ, розмістивши результати обчислень у комірки G3,
H3, I3, J3, K3, L3 відповідно (рис.2).
5. Перевіримо систему факторів на
мультиколінеарність, зробивши розрахунки згідно алгоритму Фаррара-Глобера:
5.1. Побудуємо кореляційну матрицю системи факторів 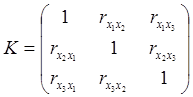 і запишемо її у
діапазоні I7:К9;
і запишемо її у
діапазоні I7:К9;
5.2. Знайдемо
визначник матриці |R| і запишемо результат у комірці I11, використовуючи
вбудовану функцію МОПРЕД;
5.3. Знайдемо розрахункове значення критерію ![]() за формулою
за формулою 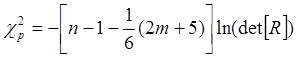 , де n - обсяг вибірки (n=20), m - число факторів моделі
(m=3), ввівши у комірку I13 формулу I1:=(-(A21-1-(11/6))*LN(I11));
, де n - обсяг вибірки (n=20), m - число факторів моделі
(m=3), ввівши у комірку I13 формулу I1:=(-(A21-1-(11/6))*LN(I11));
5.4. Знайдемо табличне (критичне) значення критерію ![]() і запишемо результат у
комірці I14, використовуючи вбудовану функцію ХИ2ОБР (імовірність
a=0,05, число ступенів вільності
k=m(m-1)/2=3(3-1)/2=3).
і запишемо результат у
комірці I14, використовуючи вбудовану функцію ХИ2ОБР (імовірність
a=0,05, число ступенів вільності
k=m(m-1)/2=3(3-1)/2=3).
6. Зробимо висновки.
7. Знайдемо матрицю С=R-1,
обернену до матриці R, записавши її у діапазоні I19:К21, використовуючи
вбудовану функцію МОБР (рис.3).Нагадуємо, як користуватися
матричними функціями пакету EXEL, зокрема, функцією МОБР. Записуємо у
комірку I19 формулу: I19: =МОБР(I7:K9).
Тепер при натиснутій лівій кнопці миші помічаємо блок клітинок I19:К21, де повинна бути обернена матриця, відпускаємо кнопку миші і
натискаємо комбінацію клавіш F2 та Ctrl+Shift+Enter. Отримаємо у виділеному
діапазоні результат дії матричної функції.
8. Розрахуємо F-статистики для факторів X1, X2, X3
за формулою 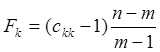 , де ckk
– елементи головної діагоналі матриці С, записавши отримані результати у
комірки Н24, I24, J24 відповідно. Для цього у комірку Н24 ввести формулу
Н24:=(I19-1)*(20-3)/(3-1); I24:=(J20-1)*(20-3)/(3-1), J24:=(K21-1)*(20-3)/(3-1)
(рис.3).
, де ckk
– елементи головної діагоналі матриці С, записавши отримані результати у
комірки Н24, I24, J24 відповідно. Для цього у комірку Н24 ввести формулу
Н24:=(I19-1)*(20-3)/(3-1); I24:=(J20-1)*(20-3)/(3-1), J24:=(K21-1)*(20-3)/(3-1)
(рис.3).
9. У комірці I26 знайдемо табличне (критичне)
значення Fкр, використовуючи
вбудовану функцію FРАСПОБР (імовірність a=0,05,
число ступенів вільності k1=m=3 й k2=n-m-1=20-4=16).
10. Зробимо висновки про
мультиколінеарність факторів X1,
X2, X3 .
11. Визначимо мультиколінеарні
пари факторів за допомогою t-статистики (критерію Стьюдента). Для цього:
11.1 Розрахуємо коефіцієнти кореляції між парами факторів за
формулою: 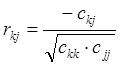 , де сkj
-елемент матриці С, що знаходиться у к-му рядку й j-ому стовпці, cкк й cjj
- діагональні елементи матриці С.
Запишемо отримані результати у комірки Н30, I30, J30 відповідно. Для цього у комірку Н30 введемо формулу
Н30:=-J19/КОРІНЬ(I19*J20), I30:=-K19/КОРІНЬ(I19*K21);
J30:=-I20/КОРІНЬ(J20*K21), використовуючи вбудовану функцію КОРЕНЬ;
, де сkj
-елемент матриці С, що знаходиться у к-му рядку й j-ому стовпці, cкк й cjj
- діагональні елементи матриці С.
Запишемо отримані результати у комірки Н30, I30, J30 відповідно. Для цього у комірку Н30 введемо формулу
Н30:=-J19/КОРІНЬ(I19*J20), I30:=-K19/КОРІНЬ(I19*K21);
J30:=-I20/КОРІНЬ(J20*K21), використовуючи вбудовану функцію КОРЕНЬ;
11.2. Розрахуємо значення t-статистик за формулою 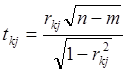 , де rkj
- коефіцієнти кореляції між парами факторів. Запишемо отримані результати
у комірки Н31, I31, J31 відповідно. Для цього у комірку Н31 введемо формулу
Н31:=H30*КОРІНЬ(20-3)/КОРІНЬ(1-H30^2); I31:=I30*КОРІНЬ(20-3)/КОРІНЬ(1-I30^2);
J31:=J30*КОРІНЬ(20-3)/КОРІНЬ(1-J30^2), використовуючи вбудовану функцію
КОРІНЬ;
, де rkj
- коефіцієнти кореляції між парами факторів. Запишемо отримані результати
у комірки Н31, I31, J31 відповідно. Для цього у комірку Н31 введемо формулу
Н31:=H30*КОРІНЬ(20-3)/КОРІНЬ(1-H30^2); I31:=I30*КОРІНЬ(20-3)/КОРІНЬ(1-I30^2);
J31:=J30*КОРІНЬ(20-3)/КОРІНЬ(1-J30^2), використовуючи вбудовану функцію
КОРІНЬ;
 11.3. У комірці I32 обчислимо
табличне (критичне) значення t-статистики, використовуючи вбудовану функцію СТЬЮДРАСПОБР
(імовірність a=0,05, число ступенів
вільності k=n-m-1=20-4=16).
11.3. У комірці I32 обчислимо
табличне (критичне) значення t-статистики, використовуючи вбудовану функцію СТЬЮДРАСПОБР
(імовірність a=0,05, число ступенів
вільності k=n-m-1=20-4=16).
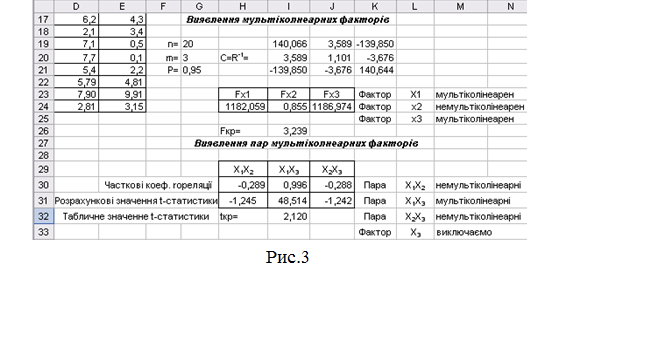
12. Порівняємо отримані
результати та зробимо висновок (рис.3).
13. Визначимо оцінки параметрів
моделі, використовуючи алгоритм стандартизованої моделі з β
-коефіцієнтами:
13.1. Запишемо у діапазоні В39:С40 кореляційну матрицю без
коефіцієнта кореляції вилученого фактора Х3: 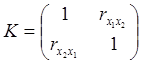 ;
;
13.2. Знайдемо визначник матриці |К| і запишемо результат у
комірці В42, використовуючи вбудовану функцію МОПРЕД;
13.3. Знайдемо матрицю С=К-1, обернену матриці
К записавши її у діапазоні В46:С47,
використовуючи вбудовану функцію МОБР;
13.4. У комірки В49 й В50 скопіюємо значення парних коефіцієнтів кореляції r(YХ1) і r(YХ2) відповідно;
13.5. Обчислимо β-коефіцієнти за формулою : 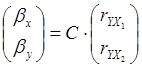 , використовуючи вбудовану функцію МУМНОЖ,
результат обчислень запишемо у діапазоні В54:В55 (рис.4).
, використовуючи вбудовану функцію МУМНОЖ,
результат обчислень запишемо у діапазоні В54:В55 (рис.4).
14. Обчислимо коефіцієнт детермінації за формулою: ![]() , ввівши у комірку В57 формулу В57:=B54*B49+B55*B50.
, ввівши у комірку В57 формулу В57:=B54*B49+B55*B50.
15. Перевіримо значимість
відмінності від нуля b-коефіцієнтів за критерієм Стьюдента:
15.1. Обчислимо значення ![]() за формулою:
за формулою: 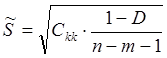 , де ckk
– елементи головної діагоналі матриці С, n – об’єм вибірки (n=20), m
- число факторів моделі (m=2) , записавши
отримані результати у комірки Е54 й Е55 відповідно. Для цього у комірку Е54
введемо формулу Е54:=КОРІНЬ(B46*(1-B57)/17), Е55:=КОРІНЬ(З47*(1-B57)/17);
, де ckk
– елементи головної діагоналі матриці С, n – об’єм вибірки (n=20), m
- число факторів моделі (m=2) , записавши
отримані результати у комірки Е54 й Е55 відповідно. Для цього у комірку Е54
введемо формулу Е54:=КОРІНЬ(B46*(1-B57)/17), Е55:=КОРІНЬ(З47*(1-B57)/17);
15.2. Обчислимо розрахункові значення t-статистик за
формулою: tр = | b|/S , записавши
отримані результати у комірки Е56 й Е57 відповідно. Для цього у комірку Е56
введемо формулу Е56: =ABS(B54)/E54,
Е57:=ABS(B55)/E55;
15.3. У комірці Е58 обчислимо табличне (критичне) значення
t-статистики, використовуючи вбудовану функцію СТЬЮДРАСПОБР
(імовірність a=0,05, число ступенів
вільності k=n-m-1=20-2-1=17).
15.4. Порівняємо отримані результати та зробити економічний
висновок.
16. Запишемо отриману
стандартизовану модель у діапазоні G39:L39 (рис.4).
17. Перейдемо від
стандартизованої моделі до нормалізованої виду: y = a0 + a1x1
+ a2x2 +...+ amxm:
17.1.
Визначимо оцінки параметрів a1,a2,...,am за
формулою: 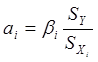 , записавши отримані результати у комірки Н43 і Н44
відповідно. Для цього введемо формули: Н43:=B54*B24/C24, Н44: =B55*B24/D24;
, записавши отримані результати у комірки Н43 і Н44
відповідно. Для цього введемо формули: Н43:=B54*B24/C24, Н44: =B55*B24/D24;
17.2. Визначимо оцінку
параметра a0 за
формулою : a0=Yсред-a1X1сред-a2X2сред, ввівши у комірку Н45
формулу Н45:=B22-H43*C22-H44*D22;
17.3. Запишемо отримане рівняння залежності у діапазоні G47:N47(рис.4).
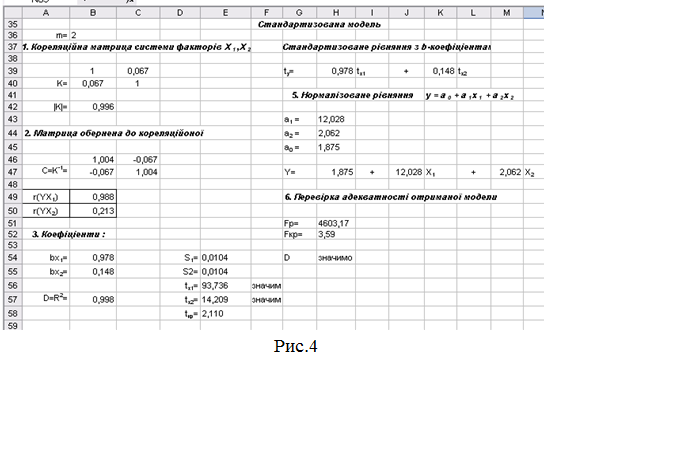
Для перевірки адекватності
отриманої моделі (значимості відмінності від нуля D) застосуємо критерій
Фішера.
18. Обчислимо розрахункове
значення критерію Фішера за формулою: 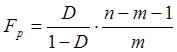 . Для цього введео у
комірку Н51 формулу Н51:=B57/(1-B57)*(17/2).
. Для цього введео у
комірку Н51 формулу Н51:=B57/(1-B57)*(17/2).
19. У комірці Н52 обчислимо
табличне значення критерію Фішера,
використовуючи вбудовану функцію FРАСПОБР (імовірність a=0,05,
число ступенів вільності k1=m=2 й k2=n-m-1=20-2-1=17)
(рис.4).
20. Порівняємо отримані
результати та зробимо висновок про адекватність моделі експериментальним даним.
21. Підвести підсумки
лабораторної роботи і зробити висновки.
22. Зберегти книгу у своїй
робочій папці під ім'ям Лаб.5.
Висновки:
1.
Між факторами Х1 і Х3 існує
мультіколінеарність, тому один з факторів (Х3) не включаємо в
множинну лінійну регресію.
2.
Використовуючи t-критерій перевірили значущість b
коефіцієнтів та побудували
стандартизовану модель tY = 0,835*tx1 + 0,625*tx2.
3.
Визначили оцінки параметрів a1,
a2 при xi
та оцінку параметру а0.
Рівняння залежності має вигляд Y = 4,51 + 11,48*X1 + 8,60*X2.
4.
Оскільки Fроз>Fтаб, то з надійністю Р=0,95 побудовану
математичну модель можна вважати адекватною експериментальним даним і на
підставі прийнятої моделі можна проводити економічний аналіз.
Завдання до лабораторної роботи №5
|
Варіант 1 |
Варіант 2 |
Варіант 3 |
|||||||||
|
X1 |
Х2 |
Х3 |
Y |
X1 |
Х2 |
Х3 |
Y |
X1 |
Х2 |
Х3 |
Y |
|
4,5 |
9,8 |
4,4 |
95,8 |
3,4 |
6,5 |
3,5 |
83,9 |
8,8 |
1,6 |
8,5 |
94 |
|
6,3 |
2,9 |
6,6 |
92,1 |
9,7 |
3,2 |
9,5 |
152,9 |
9,2 |
9,1 |
9,1 |
121,4 |
|
8,1 |
5,4 |
7,6 |
118,6 |
7,2 |
9,5 |
7,1 |
150,2 |
8,4 |
6,1 |
8,7 |
107,1 |
|
7,2 |
4,3 |
7,4 |
107,3 |
2,2 |
3,6 |
1,7 |
47,8 |
4,8 |
7,8 |
5 |
75 |
|
6,9 |
9,9 |
7,1 |
127 |
2 |
2,7 |
2,1 |
45,1 |
7,5 |
8,1 |
7,2 |
100,3 |
|
2,2 |
8,3 |
2 |
61,5 |
0,7 |
4,2 |
1 |
36,3 |
2,5 |
1,4 |
2,2 |
30,8 |
|
7,9 |
5,4 |
8,3 |
121,8 |
7,2 |
7 |
7,4 |
108,8 |
0,6 |
7,3 |
0,6 |
30,7 |
|
0 |
4,5 |
0 |
20,6 |
6,4 |
7,1 |
6,7 |
130,3 |
8,6 |
7,2 |
8,7 |
111,5 |
|
8,2 |
5,4 |
8,6 |
125,5 |
2,3 |
9,6 |
2,4 |
83,6 |
2,2 |
4,6 |
2,5 |
40,7 |
|
2,2 |
6,5 |
1,9 |
53,9 |
3,5 |
8,3 |
3,3 |
92,5 |
2,1 |
6,3 |
2,3 |
43,7 |
|
9,8 |
9,7 |
10 |
160,6 |
2 |
1,6 |
1,7 |
36,6 |
2 |
7,5 |
2,4 |
47,1 |
|
7,8 |
6,9 |
7,6 |
123,1 |
3,6 |
3 |
3,4 |
67,1 |
9,6 |
8,6 |
9,1 |
122,1 |
|
5,2 |
9,7 |
4,7 |
101,4 |
1,2 |
0,7 |
1,3 |
24,3 |
9,9 |
4,7 |
9,6 |
114,8 |
|
8,9 |
1,9 |
9 |
117,4 |
0,9 |
9,9 |
0,4 |
61,8 |
0,6 |
8 |
0,2 |
30,6 |
|
2 |
3,2 |
1,5 |
36,3 |
0 |
7 |
0,3 |
35,9 |
0,9 |
1,6 |
1,1 |
18,1 |
|
4,7 |
6,9 |
5,1 |
89,7 |
7,6 |
6,9 |
7,4 |
142,2 |
1,9 |
7,3 |
1,9 |
43,9 |
|
7,7 |
9,2 |
8,1 |
134,3 |
8,4 |
2,2 |
8,5 |
132 |
0,2 |
4,7 |
0 |
18,2 |
|
7,6 |
1,2 |
7,1 |
95,6 |
8,1 |
5,7 |
7,9 |
143,3 |
3,3 |
3,2 |
3,5 |
47 |
|
5,3 |
3,3 |
5,3 |
79,7 |
1,9 |
4,4 |
2,1 |
52,8 |
8,2 |
7 |
8,2 |
105,6 |
|
7,1 |
2,7 |
7 |
98,4 |
4,9 |
6,8 |
5,3 |
108 |
1,9 |
1,4 |
1,6 |
24,3 |
|
Варіант 4 |
Варіант 5 |
Варіант 6 |
|||||||||
|
X1 |
Х2 |
Х3 |
Y |
X1 |
Х2 |
Х3 |
Y |
X1 |
Х2 |
Х3 |
Y |
|
2,4 |
4,8 |
2,7 |
33 |
2,5 |
3,9 |
2,9 |
14,1 |
5,2 |
3 |
5,3 |
67,2 |
|
4,5 |
6,8 |
4,8 |
56,6 |
7 |
1,7 |
7 |
76,5 |
7,8 |
1,3 |
7,7 |
86 |
|
9,2 |
2,4 |
9,1 |
96,9 |
9,1 |
9,1 |
9,1 |
112,6 |
7,1 |
3,5 |
7 |
87,2 |
|
7,6 |
1,4 |
7,2 |
78,6 |
2,2 |
0,6 |
2,2 |
26,5 |
8,5 |
1,4 |
8,6 |
93,6 |
|
0,3 |
1,1 |
0,2 |
6,5 |
9,9 |
0,1 |
9,8 |
101,9 |
9,5 |
8 |
9,7 |
102,6 |
|
3,5 |
7,9 |
3,3 |
44,4 |
2 |
7,6 |
1,5 |
35,8 |
4,4 |
3,9 |
4 |
60,6 |
|
7 |
2,1 |
7,2 |
76,4 |
2,7 |
1,1 |
3,1 |
34,5 |
3,4 |
3,6 |
3,5 |
51,7 |
|
5,4 |
5,2 |
5 |
60,3 |
1,2 |
5,9 |
0,8 |
24,9 |
3,2 |
0,3 |
2,8 |
34,1 |
|
0,9 |
8,5 |
1 |
20,8 |
5,4 |
3,2 |
5 |
61,7 |
0 |
1,8 |
0,1 |
9,9 |
|
9,3 |
6,3 |
9,1 |
100,9 |
7,3 |
2,3 |
6,8 |
77,7 |
5,7 |
5,4 |
6,1 |
83,7 |
|
8,4 |
9,6 |
8,5 |
97,4 |
1,3 |
5,1 |
1,2 |
25,4 |
5,6 |
2,1 |
5,7 |
68,2 |
|
8,6 |
3,2 |
8,3 |
90,5 |
5,3 |
3 |
5,5 |
63,4 |
9,9 |
3,5 |
9,9 |
115,9 |
|
6,3 |
5,8 |
5,8 |
69,2 |
3,6 |
6,5 |
3,5 |
51,4 |
6,5 |
2,1 |
6,9 |
78,7 |
|
9,6 |
1,5 |
9,6 |
100,1 |
3 |
7,6 |
2,9 |
47,7 |
6,9 |
2,5 |
6,6 |
80 |
|
6,6 |
4,5 |
7 |
75,6 |
0,8 |
3,6 |
0,5 |
16,4 |
4,4 |
6,3 |
4,1 |
71 |
|
6,1 |
6 |
6,1 |
70,1 |
5,8 |
4,9 |
6,2 |
73,1 |
5,1 |
9,2 |
4,6 |
88,6 |
|
1,2 |
4,1 |
0,9 |
17,4 |
1,5 |
3,9 |
1,5 |
26,1 |
1 |
0,4 |
1,1 |
15,2 |
|
4,6 |
5,2 |
4,9 |
55,9 |
1,9 |
7,6 |
1,8 |
36,7 |
5,7 |
4,5 |
6,1 |
79,6 |
|
7,1 |
9,4 |
7 |
84,4 |
9,6 |
1,5 |
9,8 |
103 |
3,1 |
6,3 |
3 |
58,3 |
|
9,3 |
6,7 |
9,5 |
103,4 |
6,9 |
7,2 |
7 |
87,1 |
7,7 |
7,9 |
8 |
113 |
|
Варіант 7 |
Варіант 8 |
Варіант 9 |
|||||||||
|
X1 |
Х2 |
Х3 |
Y |
X1 |
Х2 |
Х3 |
Y |
X1 |
Х2 |
Х3 |
Y |
|
2,6 |
0,9 |
2,1 |
10,5 |
2,4 |
3 |
2,1 |
22,9 |
4,5 |
5,1 |
4,5 |
62,4 |
|
1,2 |
4,1 |
1,2 |
17,2 |
8,6 |
5,7 |
8,2 |
48,2 |
3,3 |
0 |
3,6 |
44,1 |
|
3,6 |
0,5 |
3,9 |
11,8 |
1,7 |
9,4 |
1,5 |
53,6 |
3,6 |
3,3 |
3,8 |
50,2 |
|
6,2 |
9,9 |
6,3 |
45,2 |
5,5 |
9,3 |
5,4 |
60,8 |
5,6 |
7,3 |
5,2 |
75,5 |
|
9,2 |
3,1 |
9,5 |
31,4 |
8,4 |
2,8 |
8,7 |
34,1 |
3,6 |
1,4 |
3,5 |
46,7 |
|
1,5 |
4,2 |
1,5 |
18,5 |
9,3 |
1,9 |
9,3 |
31,2 |
1,6 |
3,4 |
1,3 |
24,2 |
|
0 |
4,5 |
0,1 |
16,1 |
6 |
7,2 |
5,6 |
50,3 |
1,7 |
4,5 |
1,9 |
28,7 |
|
9,6 |
0,3 |
10 |
23,4 |
5,8 |
5,2 |
5,6 |
40,5 |
5,3 |
5,8 |
5,1 |
71,3 |
|
6,8 |
1,8 |
7,2 |
22,3 |
8,7 |
7,9 |
8,9 |
60,3 |
5,4 |
8,6 |
4,9 |
73,3 |
|
5,7 |
5,6 |
6 |
31,5 |
3,4 |
4,6 |
3,4 |
33,2 |
3,5 |
5,8 |
3 |
47,3 |
|
5,7 |
8,8 |
6 |
40,6 |
5,4 |
6,7 |
5 |
46,5 |
7,1 |
6,7 |
6,6 |
92,1 |
|
2,8 |
6,4 |
3,1 |
28,2 |
8 |
4,5 |
7,6 |
41,1 |
0,8 |
3,8 |
0,7 |
15,8 |
|
2,7 |
0,6 |
2,2 |
10,1 |
5,4 |
6,8 |
5,1 |
47,8 |
9,5 |
2,8 |
9,4 |
119,3 |
|
6,5 |
2,8 |
6,8 |
25 |
8,5 |
3,1 |
8,8 |
35,8 |
4,3 |
4 |
4,6 |
60,3 |
|
9,1 |
8,5 |
9,1 |
46,5 |
3,2 |
7,8 |
2,8 |
48 |
0,5 |
7,4 |
0,5 |
16 |
|
0 |
3,8 |
0,4 |
13,9 |
1,1 |
7,6 |
0,9 |
42,7 |
8,7 |
9,4 |
8,4 |
114,6 |
|
6,4 |
5,5 |
6,3 |
32,3 |
3,2 |
0,7 |
3,6 |
13,2 |
8 |
2,5 |
7,7 |
99,4 |
|
9,1 |
2,5 |
9,3 |
29 |
4,9 |
9,1 |
4,6 |
58,4 |
1,6 |
7,2 |
1,2 |
26,8 |
|
1 |
0,8 |
0,7 |
7,4 |
5,1 |
3 |
5 |
28,4 |
5,2 |
6,4 |
4,8 |
69,8 |
|
7,5 |
0,5 |
7,9 |
19,9 |
6,5 |
7,6 |
6,3 |
54,2 |
8 |
3,1 |
7,8 |
100,9 |
|
Варіант 10 |
Варіант 11 |
Варіант 12 |
|||||||||
|
X1 |
Х2 |
Х3 |
Y |
X1 |
Х2 |
Х3 |
Y |
X1 |
Х2 |
Х3 |
Y |
|
7,6 |
4 |
7,5 |
76,2 |
8,4 |
4,5 |
8,2 |
82,6 |
1,7 |
0,6 |
1,7 |
10,5 |
|
4,6 |
8,2 |
4,4 |
87,6 |
8,5 |
8,1 |
8,2 |
94,3 |
6,3 |
9,2 |
6,7 |
38 |
|
5,6 |
8,4 |
5,5 |
95,2 |
2,9 |
4,4 |
2,4 |
37,1 |
0,4 |
7,8 |
0,4 |
12,7 |
|
2,7 |
2,9 |
3 |
40,3 |
8,2 |
3,4 |
8,1 |
77,9 |
2,5 |
3,6 |
2,6 |
16,7 |
|
2,3 |
2,3 |
2,2 |
32,7 |
7,3 |
4,7 |
7,2 |
75,4 |
7,6 |
2,9 |
7,7 |
36,5 |
|
1,6 |
1,8 |
2 |
26,6 |
6 |
8,7 |
5,6 |
75,5 |
3 |
2,9 |
2,5 |
16,5 |
|
6,5 |
4,9 |
6,3 |
75,4 |
0,1 |
1,6 |
0,1 |
8,8 |
6,7 |
6,9 |
6,4 |
36,3 |
|
2,2 |
1,5 |
2,6 |
27,8 |
7,3 |
2,5 |
6,9 |
67,7 |
8,1 |
0,7 |
7,9 |
36 |
|
7 |
6,5 |
7,4 |
91,2 |
9,8 |
2,7 |
9,4 |
87,4 |
1,3 |
2,4 |
1,6 |
10,8 |
|
7,7 |
2,5 |
7,5 |
66,2 |
0,3 |
7,7 |
0,3 |
28,7 |
1 |
4,6 |
0,7 |
11,1 |
|
8 |
3,9 |
8,1 |
78,4 |
0,3 |
2 |
0,4 |
11,5 |
0,3 |
8,4 |
0,1 |
12,6 |
|
9,2 |
4,1 |
9 |
86 |
0,7 |
5,7 |
0,2 |
23,6 |
2,3 |
1,1 |
1,8 |
12 |
|
3,7 |
5,2 |
3,6 |
61 |
5,4 |
4,7 |
5,3 |
59,5 |
2,5 |
5,3 |
2,4 |
17,7 |
|
0,5 |
9,6 |
0,2 |
72,4 |
6,8 |
2 |
7 |
64,3 |
5,4 |
0,9 |
5 |
24,9 |
|
3,5 |
5,1 |
3,2 |
59 |
4,2 |
2,8 |
3,9 |
43,9 |
2,1 |
9,8 |
2,1 |
20,9 |
|
2,7 |
1,2 |
2,5 |
27,3 |
4,7 |
1 |
4,5 |
42,8 |
1,5 |
3,1 |
1,8 |
12,4 |
|
7 |
9,5 |
7 |
111,7 |
6,1 |
9,3 |
6,3 |
80,5 |
3,3 |
0,2 |
3,6 |
16,8 |
|
0,1 |
4,9 |
0,3 |
38,3 |
3,1 |
0,9 |
3,3 |
30,9 |
4,1 |
1,1 |
3,9 |
20,5 |
|
8,9 |
0,9 |
8,9 |
63 |
5,3 |
4 |
4,9 |
55,4 |
5,4 |
1 |
5,7 |
26,3 |
|
4,2 |
5,8 |
4,2 |
68,4 |
8,3 |
8,8 |
8,1 |
95,6 |
4,6 |
7 |
5 |
29,4 |
|
Варіант 13 |
Варіант 14 |
Варіант 15 |
|||||||||
|
X1 |
Х2 |
Х3 |
Y |
X1 |
Х2 |
Х3 |
Y |
X1 |
Х2 |
Х3 |
Y |
|
3,2 |
1,2 |
3,5 |
27 |
6,5 |
7,7 |
6,7 |
86,9 |
7,3 |
3,6 |
7,1 |
86,1 |
|
7,6 |
0,7 |
7,2 |
49,7 |
9,3 |
6,1 |
8,9 |
100,4 |
7,1 |
4,8 |
7,3 |
94,4 |
|
5,5 |
1,2 |
5,8 |
40,6 |
9,3 |
7,9 |
9,6 |
110,5 |
1 |
8 |
1,4 |
68,1 |
|
4,3 |
0,3 |
4,2 |
29,2 |
2,9 |
2,4 |
3 |
36,2 |
0,2 |
4,2 |
0,1 |
33,6 |
|
3,6 |
5,2 |
3,9 |
40,6 |
3,7 |
3,5 |
3,3 |
44,5 |
4,9 |
6,1 |
4,5 |
83,7 |
|
0,9 |
5,3 |
1 |
24,3 |
8,3 |
1,8 |
8,1 |
75,6 |
0 |
9,8 |
0,4 |
70,6 |
|
0 |
5,9 |
0,1 |
20,5 |
4,6 |
9,5 |
4,8 |
78,3 |
3,7 |
0,1 |
4,1 |
34,6 |
|
1,8 |
6 |
2,1 |
33,1 |
2,3 |
7 |
2,9 |
53 |
8,1 |
6,7 |
8,3 |
115,5 |
|
7,5 |
7,4 |
7,3 |
69,9 |
7,3 |
2,7 |
7,1 |
71 |
2,3 |
4 |
2,3 |
49,3 |
|
4,3 |
6,8 |
4,3 |
49,3 |
5,2 |
4,8 |
5,5 |
65,2 |
8,8 |
3,6 |
8,7 |
98,3 |
|
3,8 |
0,3 |
4,1 |
27,9 |
2 |
6,1 |
1,9 |
42,7 |
0,8 |
8 |
0,5 |
64,5 |
|
3 |
0,6 |
3,3 |
24,1 |
3,6 |
0,8 |
3,4 |
34,3 |
4 |
8,3 |
3,6 |
91,8 |
|
7 |
6,5 |
7,3 |
65,4 |
9,3 |
4,1 |
9,3 |
94 |
9,3 |
3,6 |
9,4 |
102,9 |
|
5,4 |
4,6 |
5,6 |
49,4 |
7,7 |
4,5 |
7,3 |
80,7 |
8,5 |
2,7 |
8 |
87,6 |
|
0,2 |
4,3 |
0,6 |
17,9 |
4,8 |
7,6 |
4,5 |
70,9 |
3,1 |
9 |
3,2 |
91,1 |
|
6,7 |
4,6 |
6,7 |
56,5 |
5 |
4,2 |
4,7 |
58,6 |
4,6 |
7,3 |
4,8 |
91,2 |
|
6,7 |
3,5 |
6,9 |
53,8 |
4,3 |
8,8 |
4,1 |
71,6 |
7,8 |
3,5 |
8,2 |
91,5 |
|
4,6 |
0,4 |
4,2 |
30,4 |
5,9 |
2,4 |
5,6 |
58,4 |
7 |
6,5 |
7 |
104,4 |
|
5 |
0,3 |
4,6 |
33,1 |
8,8 |
6,4 |
8,4 |
97,2 |
4 |
3 |
4,4 |
57,4 |
|
4,4 |
0,8 |
4,4 |
32 |
8,3 |
0,3 |
7,9 |
69,2 |
8,6 |
4 |
9 |
101,8 |

