ЛАБОРАТОРНА РОБОТА № 4

 

Тема: Виробнича функція Кобба-Дугласа.

Мета заняття: Модель обсягу випуску продукції має вигляд:,

де - обсяг випущеної продукції, - працезатрати; - основні засоби розглянутої галузі.

На основі статистичних даних, з використанням  методу МНК, знайти:

ü оцінки параметрів виробничої функції , , ;

ü з надійністю P=0,95 встановити адекватність прийнятої моделі статистичним даним та знайти значення прогнозу  і його надійний інтервал;

ü побудувати ізокванту , де - одне із значень планового обсягу випуску продукції;

ü використовуючи розрахунки, зробити висновки.

 

Хід роботи

Висувається гіпотеза, що модель обсягу випуску продукції має вигляд:,

де - обсяг випущеної продукції, - працезатрати; - основні засоби розглянутої галузі.

1.      Завантажити програму EXCEL.

2.      Сформуємо таблицю вихідних даних, для цього заповнємо діапазон комірок B3:D13. Третій рядок виділено для заголовків.

3.      Перетворені змінні    розмістити відповідно в блоках E4:E13,  F4:F13,  G4:G13. Для обчислення значень у цих блоках використовують вбудовану математичну функцію LN.

Нагадаємо, що для того, щоб заповнити блок комірок однотипними формулами, необхідно виконати наступну послідовність дій:

- ставиться курсор у комірку E4 і в командний рядок вводимо формулу Е4:=LN(B4 );

- після того, як формулу введено до комірки E4, клацаємо ще раз по цій комірці, підводимо курсор миші у лівий нижній куток до утворення знаку “+” і, зачепивши за нього і задержуючи натиснутою ліву кнопку миші, протягнемо курсором до кінця блоку E4:E13; якщо відпустити кнопку миші, в блоці E4:E13 буде отримано  потрібний діапазон формул;

- аналогічно заповнюємо відповідними формулами блоки F4:F13 та G4:G13. 

 В14-му рядку будуть розміщені суми по відповідним стовбцям. Для цього:

- ставимо курсор миші у комірку B14 і вводимо формулу B14:=СУММ(B4:B13);

 - зачепивши лівою кнопкою миші за лівий нижній куток комірки B14, протягуємо цю формулу на увесь блок B14:G14.

4.      Перетворені значення використовуємо для складання системи нормальних рівнянь. Симплекс-таблиця для зведеної системи нормальних рівнянь в електронній таблиці, що розміщена в блоці A17:E21 матиме вигляд:

Цю таблицю використовуємо для отримання вектора оцінок параметра моделі. Для цього використовуємо матричні функції, що є в пакеті EXEL.

5.  Для отримання матриці, оберненої до матриці системи нормальних рівнянь, ставимо курсор у комірку C22 і вводимо формулу C22: =МОБР(B18:D20). Після натискання клавіші “Enter” у комірці C22 буде відображено лівий верхній елемент матриці. Щоб отримати всю матрицю, відмічаємо при натиснутій лівій кнопці миші весь блок C22:E24, де буде знаходитися обернена матриця,  і натискаємо комбінацію кнопок Ctrl+Shift+Enter.

Зауваження: надалі будемо пам’ятати, що термін «ввести матричну функцію» означає вище наведену послідовність дій.

6.  У блоці G22:G24 треба отримати вектор-стовпець оцінених параметрів , , . Для цього використовуємо матричну функцію МУМНОЖ. Ставимо курсор миші у комірку G22 і вводимо формулу G22:=МУМНОЖ(C22:E24;E18:E20), а далі, аналогічно до попереднього пункту, відмічаємо мишею блок G22:G24 і натискаємо комбінацію кнопок Ctrl+Shift+Enter.

7.      Тепер ми маємо значення оцінок параметрів моделі і в блоці H4:H13 за формулою лінійної регресії обчислюємо розрахункове значення показника .

Для цього:

-          ставимо курсор у комірку H4 і вводимо формулу  H4:= $G$22+$G$23*E4+$G$24*F4;

-          при натиснутій кнопці миші протягуємо цю формулу на блок H4:H13.

8.      Знайдемо розрахункове значення  показника   з використанням вбудованої математичної функції EXP та значень блоку H4:H13. Для цього у комірку I4 вводимо формулу I4:=EXP(H4) та протягуємо її на блок I4:I13.

9.      Для визначення адекватності побудованої математичної моделі експериментальним даним обчислюємо  та .  Для цього обчислюємо значення квадратів відхилень фактичних значень показника від розрахункових та середніх значень показника:

-  у комірку J4 вводимо формулу J4: =D4-I4 і протягуємо її на увесь блок J4:J13;

- у комірку K4 вводимо формулу K4:=J4^2  і протягуємо її на увесь діапазон  K4:K13;

- у комірку L4  вводимо формулу L4: =(D4-СРЗНАЧ($D$4:$D$13))^2 (в цій формулі для обчислення середнього значення блоку D4:D13 використовується вбудована статистична функція  СРЗНАЧ(блок) – середнє статистичне значення блоку;

-  аналогічно обчислюємо квадрати відхилень розрахункових значень показника від середніх в діапазоні M4:M13.

Для контролю можна в діапазоні N4:O13 зробити відповідні розрахунки і для допоміжної змінної .

10.  Поставимо курсор в клітинку G14 і протягнемо формули сумування на діапазон  G14:O14.

11.  Дисперсію помилок та дисперсію показника обчислюємо в комірках I16 та K16 відповідно. Там розміщуємо формули I16:=$K$14/($C$15-3)  та K16:=$L$14/($C$15-1).

12.  Коефіцієнти детермінації та кореляції обчислюються в комірках I18 та I19. Для цього в комірку I18 вводимо формулу I18:=($K$16-$I$16)/$K$16, а у комірку I19: =КОРЕНЬ(I18).

13.   Розрахункове значення критерію Фішера обчислюється у клітинці  J20, в цій комірці поміщено формулу J20:=(M14/2)/I16.  Можна скористатися вбудованою функцією FРАСПОБР і поруч вивести табличне значення розподілу Фішера для заданих степенів вільності та рівня довіри p=0,95, який вказано в комірці L21.  Тобто, у комірку L22 поміщено формулу L22:=FРАСПОБР(1-K21;2;C15-3).  Оскільки ,  то можна зробити висновок про адекватність моделі.

14. 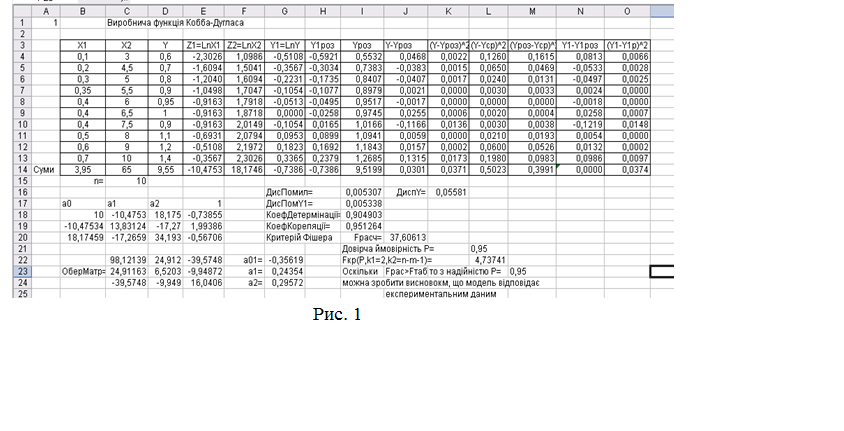 Лист розрахунків EXEL після виконаних дій буде виглядати подібним чином:

Знайдемо прогнозні значення показника та довірчі інтервали для прогнозного значення показника.

 

15.  У комірки E27 та H27 введемо прогнозні значення факторів  та . У комірках E28 та E28 обчислимо значення допоміжних змінних  та , ввівши у відповідні комірки формули: E28:=LN(E27) та E28:=LN(H27).

16.  Точковий прогноз для показників  та  обчислюємо у комірках H29 та E29, ввівши у відповідні комірки формули E29:=EXP(G22)*(E27^G23)*(H27^G24)” та H29:=$G$22+$G$23*E28+$G$24*$H$28.

17.  У блоці C30:C32 ще раз запишемо матрицю прогнозних значень фактору  для того, щоб отримати матрицю , транспоновану до   в діапазоні E31:G31. Використовуючи вбудовану функцію ТРАНСП, у діапазон E31:G31 вдедемо формулу: =ТРАНСП(C30:C32).

18.  Матрицю  знаходимо  за допомогою вбудованої функції МУМНОЖ – матричного добутку, ввівши до блоку  K31:M31 формулу:=МУМНОЖ(E31:G31;C22:E24).

19.  Стандартну помилку прогнозу знаходимо теж за допомогою функції матричного добутку в клітинці L32, за формулою L32:=КОРЕНЬ(I17)*КОРЕНЬ(1+МУМНОЖ(K31:M31;C30:C32)).

20.  Стандартну помилку використовуємо  для побудови довірчого інтервалу для показника  у діапазоні  J33:L33. Для цього вводимо формули у відповідні комірки:

-          J33: =$H$29-СТЬЮДРАСПОБР(2*(1-$К$21);$C$15-3)*$L$32;

-          L33: =$H$29+СТЬЮДРАСПОБР(2*(1-$К$21);$C$15-3)*$L$32.

21.   Довірчий  інтервал для  будуємо з використанням функції EXP у діапазоні  J34:L34. Для цього вводимо формули у відповідні комірки:

-          J34:=EXP(J33);

-          L34:=EXP(L33).

Для наочного уявлення взаємозамінюваності факторів побудуємо ізокванти.

22.  Значення оцінки параметра 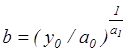, визначається у комірці C38 за формулою: C38:=(E37/EXP(G22))^(1/G23).

23.   Змінна  залежність основних засобів від працезатрат – змінної , що знаходиться у блоці C40:C49,  обчислюється  за формулою:  в блоці B40:B49. Так, у комірку B40 вводимо формулу : B40: =$C$38/(C40^($G$24/$G$23)). Як відомо, знак “$” вказує на абсолютну адресацію до цієї комірки.

24.  Для того, щоб побудувати графік ізокванти , викликаємо майстер діаграм і в полях значення для X, значення для Y вказуємо діапазони C40:C49 та B40:B49 відповідно (див. Лаб.1).

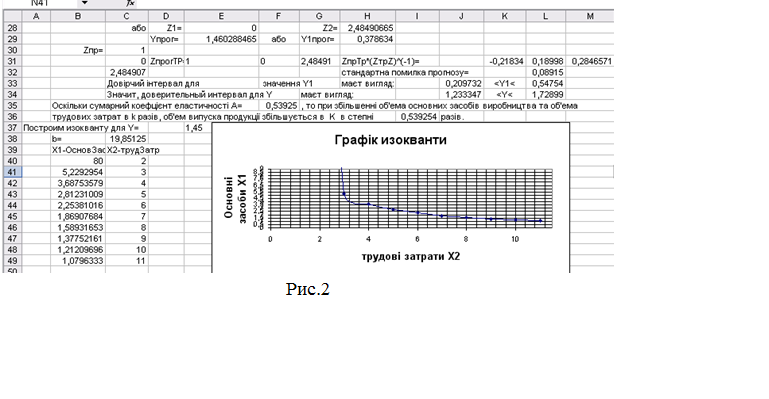
Вид робочого листа EXEL з результатами останніх обчислень представлено на рис.2.

25.  Підвести підсумки лабораторної роботи і зробити висновки.

26.  Зберегти книгу у своїй робочій папці під ім'ям Лаб.4.

 

Висновки.

1.      Знайдено математичну модель залежності обсягу продукції від працезатрат та основних засобів виробництва у вигляді виробничої функції  з оцінками коефіцієнтів -035619; 0,24354; 0,29572.

2.      На основі коефіцієнта детермінації та критерію Фішера зроблено висновок про адекватність моделі.

3.      Параметри 0,24354 та 0,29572 є частинними коефіцієнтами еластичності, тобто зміна фактору  (працезатрати) на 1% при незмінному факторі (основні засоби) викликає зміну обсягу випуску продукції на 0,244%, аналогічно  зміна фактору  на 1% при незмінному факторі  викликає зміну обсягу випуску продукції на 0,296%.

4.      Темпи приросту показника виражаються лінійно через темпи приросту факторів

,

де -темпи приросту показника і факторів відповідно.

5.      Для значень факторів =1 та =12 визначено точковий прогноз ,  та 95% довірчий інтервал для прогнозованого значення показника .

6.      Оскільки сумарний коефіцієнт еластичності  , це означає що при збільшенні обсягу факторів виробництва  і  у  разів, обсяг випуску продукції збільшиться у  разів.