ЛАБОРАТОРНА
РОБОТА №3
Тема: Побудова та аналіз
однофакторної моделі.
Мета заняття: Задана вибірка, яка отримана для двох факторів X й Y.
Необхідно:
ü висунути гіпотезу про вид залежності;
ü побудувати модель даної залежності;
ü перевірити значимість
відмінності від нуля отриманих оцінок коефіцієнтів 
та 
, використовуючи
t-статисту Стьюдента;
ü перевірити адекватність отриманої залежності за критерієм
Фішера;
ü використовуючи коефіцієнт еластичності провести економічний
аналіз впливу фактора x на показник y.
Хід роботи
1.
Завантажити програму EXCEL.
2.
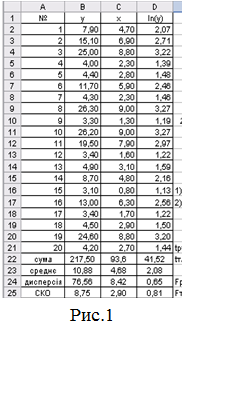
Сформувати таблицю вихідних даних, заповнивши діапазон
комірок А2:C21 (рис.1).
3.
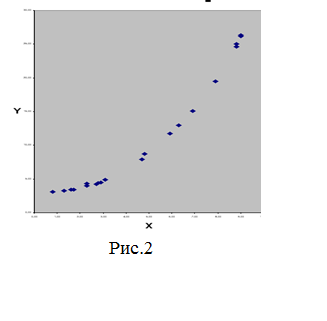
За допомогою майстра побудови діаграм побудувати кореляційне
поле даної статистичної вибірки (див. рис.2)
4.
По виду кореляційного
поля ( так як з ростом х - у в основному збільшується) припускається
наявність залежності двох типів:
- лінійної
;
-
експоненціальної 
(рис. 2).
5.
Для побудови гіпотези про вид залежності необхідно виконати
розрахунки:
5.1. У комірці
В27 за допомогою вбудованої функції СЧЕТЗ знайдемо об’єм вибірки n;
5.2. Розрахуємо
значення натурального логарифма величини y,
використовуючи вбудовану функцію LN і результати обчислення
розмістимо у діапазоні D2:D21;
5.3.
Розрахуємо суму величин 
, 
та 
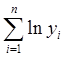, використовуючи вбудовану функцію СУММ або Автосумму;
5.4. Розрахємо середнє значення величин y,
x, ln(y), використовуючи
вбудовану функцію СРЗНАЧ;
5.5.
Розрахуємо дисперсію величин y, x, ln(y), використавши при цьому вбудовану
функцію ДИСП;
5.6.
Розрахуємо середнє квадратичнє відхилення (СКВ) величин y, x, ln(y), як корінь квадратний з дисперсій відповідних величин,
використавши при цьому вбудовану функцію КОРЕНЬ (рис. 1).
6.
Обчислимо вибіркові парні
коефіцієнти кореляції між x й y та x
й Ln(y) за формулою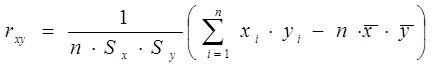 
, або використовуючи вбудовану функцію КОРРЕЛ,
розмістивши результати обчислень у комірках F3, G3 відповідно (рис. 3).
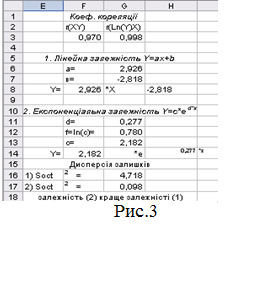
За знайденими значеннями
коефіцієнтів зробити висновки.
7.
Обчислимо для одержання лінійної залежності
величин x й y: Y=ax+b, коефіцієнти а й b
за формулами: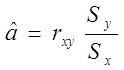 
і 
, зробивши наступне:
- розрахуємо
коефіцієнт a, ввівши у комірку G6
формулу G6:=F3*(B25/C25);
-
розрахуємо
коефіцієнт b , ввівши у комірку G7
формулу G7:=B23-(G6*C23).
8.
Записати отриману
лінійну залежність у діапазоні Е8:I8 (рис.3).
9.
Для одержання експоненціальної залежності величин x та y:
Y=c*ed*X необхідно
розрахувати коефіцієнти c й d. Перед цим прологарифмуємо рівняння: ln(Y)=ln(c)+d*X і здійснивши відповідні
заміни z=ln(Y) і f=ln(c), одержимо лінійну залежність виду z=f+dх. Розрахуємо коефіцієнти f
й d (використаємо аналогічні формули
для лінійної залежності):
- розрахуємо
коефіцієнт d, ввівши у комірку G11
формулу G11:=G3*(D25/C25);
- розрахуємо
коефіцієнт f, ввівши у комірку G12 формулу
G12:=D23-(G11*C23).
10. Так як f=ln(c), то 
, то розрахуємо оцінку параметра с, ввівши у комірку G13 формулу G13:=EXP(G12), використовуючи
вбудовану функцію EXP.
11.Записати отриману експоненціальну
модель у діапазоні Е14:I14 (рис.3).
12.
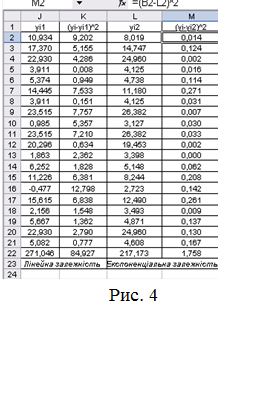Обчислимо розрахункове
значення yi1розр для лінійної залежності Y=aх+b. Для цього у комірку J2 ввести
формулу J2: =$G$6*C2+$G$7, використовуючи абсолютне посилання для комірок G7 и G6.
13. Використовуючи операцію автозаполнення,
скопіювати формулу у діапазон J3:J21.
14.Стовпець К розрахуємо як квадрат
різниці (yi - yi1розр)2
, ввівши у комірку К2 формулу К2:=(В2-J2)^2. Використовуючи операцію
автозаполнения, скопіювати формулу у діапазон К3:К21.
15.Обчислимо розрахункове значення yi2розр для експоненціальної
залежності Y=c*ed*X. Для
цього у комірку L2 введемо формулу L2:=$G$13*(EXP($G$11*C2)), використовуючи
вбудовану функцію EXP й абсолютне посилання для комірок G13 и G
11.
16.Стовпець M розрахуємо як квадрат
різниці (yi - yi2розр)2 , ввівши у комірку M2 формулу M2.
Використовуючи операцію автозаполнення, скопіювати формулу у діапазон M3:M21.
17.У комірках K22 й M22 розрахуємо суму
всіх значень yi1розр й yi2розр, використовуючи
вбудовану функцію СУММ або Автосумму (рис. 4).
18.Розрахуємо дисперсії залишків для
лінійної й експоненціальної залежностей, використовуючи формулу: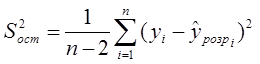 
. Для цього у комірку G16 введемо формулу G16:=К22/(В27-2), а
у комірку G17:=М22/(В27-2) (рис.3).
19.Порівняємо дисперсії залишків даних
залежностей. Тепер можна зробити висновок про те, яка модель краще відображає
задану залежність.
Перевіримо, що знайдений коефіцієнт кореляції значимо
відрізняється від нуля. Для цього використаємо критерій Стьюдента.
20.Знайдемо розрахункове значення
критерію Стьюдента, використовуючи формулу: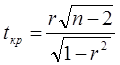 
. Для цього у комірку F21 ввести формулу
F21:=G3*КОРЕНЬ(В27-2)/КОРЕНЬ(1-(G3)^2), використовуючи вбудовану функцію
КОРЕНЬ.
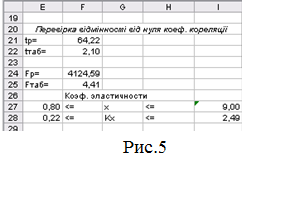
21.У комірці F22 обчислимо табличне значення критерію Стьюдента, використовуючи вбудовану
функцію СТЬЮДРАСПОБР (імовірність a=0,05,
число ступенів вільності k=n-2=20-2=18).
22.Порівнявши отримані результати,
зробити висновок.
Для перевірки адекватності (тобто ступеня
відповідності побудованого рівняння регресії наявним статистичним даним)
застосуємо критерій Фішера.
23.Обчислимо розрахункове значення критерію Фішера за формулою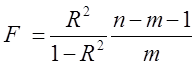 
. Для цього
введемо у комірку F24 формулу
F24:=G3^2/(1-G3^2)*(B27-2).
24.У комірці F25 необхідно обчислити
табличне значення критерію Фішера,
використовуючи вбудовану функцію FРАСПОБР (ймовірність a=0,05,
число ступенів вільності k1=m=1 й k2=n-m-1=20-2=18).
25.Порівнявши отримані результати,
зробимо висновок (рис.5).
26.Зробимо аналіз отриманої залежності,
обчисливши коефіцієнт еластичності по формулі: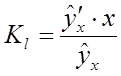 
(для експонентної
моделі використаємо формулу 
, у випадку вибору
лінійної моделі -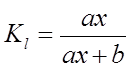 
).
27. У комірках Е28 й I28 обчислимо межі
зміни коефіцієнта еластичності Кl1 й Кl2, для цього у відповідні комірки введемо формули
Е28:=G11*E27; I28:=G11*I27, де E27– мінімальне значення для х, а I27 – максимальне, узяте з
діапазону С2:С21 (у нашому випадку використовуємо формулу для експоненціальної
моделі). Мінімальне та максимальне значення для Х з діапазону С2:С21 можна
знайти за допомогою вбудованих функцій МИН та МАКС відповідно.
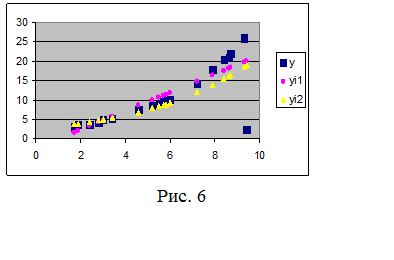
28.Для наочного уявлення розрахунків
побудувати графіки статистичних даних та побудованих залежностей (див. лаб.1).
29.Проаналізувати отримані
графіки.(рис.6).
30.Підвести підсумки лабораторної роботи
і зробити висновки.
31.Зберегти книгу у своїй робочій папці
під ім'ям Лаб.3.
Висновки:
1.
Порівнявши дисперсії залишків лінійної та експоненціальної
залежностей, можна зробити висновок, що експоненціальна модель краще відображає
задану залежність, так як дисперсія залишків експоненціальної моделі менше.
2.
При зміні фактора x
для вихідних даних в інтервалі 0,8 £ х £ 9,0 коефіцієнт еластичності буде змінюватися в межах 0,22 £ Kl £ 2,49. Таким чином, збільшення значення фактора на 1% приведе до росту
значення показника в середньому на 2,49%.
3.
Значення коефіцієнта кореляції, наближене до 1, а також
невисока величина дисперсії залишків означають тісний взаємозв'язок між
фактором і показником.
4.
Оцінка значимості відмінності від нуля параметрів рівняння й
адекватності моделі дозволяють зробити висновок, що модель можна використовувати
з метою прогнозування величини показника.
Завдання до лабораторної роботи №3
|
1 |
2 |
3 |
4 |
5 |
|||||
|
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
|
3,4 |
5,1 |
7,6 |
2,34 |
9,6 |
42,6 |
0,8 |
3,2 |
2 |
4,6 |
|
5,2 |
8,1 |
4 |
8,1 |
2,2 |
4,4 |
8 |
23,5 |
6,1 |
13,3 |
|
4 |
5,8 |
4,6 |
9,6 |
5,9 |
14,1 |
4 |
7,8 |
3,6 |
6,9 |
|
4 |
5,6 |
8,2 |
28,3 |
5,6 |
12,8 |
8,3 |
25,3 |
0,8 |
3,5 |
|
7,6 |
15,1 |
5,6 |
13 |
1,2 |
2,9 |
9,3 |
32,6 |
9,3 |
31,4 |
|
7 |
13 |
8,4 |
29,8 |
2,7 |
5,2 |
3,6 |
7,2 |
4,1 |
8,3 |
|
9 |
21,6 |
2,7 |
5,9 |
5,4 |
12,2 |
8,5 |
25,9 |
7,7 |
20,3 |
|
8,4 |
18,9 |
2,9 |
5,9 |
2,4 |
5 |
2,7 |
5,5 |
4,5 |
8,7 |
|
7,5 |
15 |
2,3 |
4,9 |
9,5 |
41,7 |
3,1 |
6,5 |
4,8 |
9,4 |
|
2 |
3,9 |
2,3 |
5,1 |
5,1 |
10,8 |
9 |
30 |
7,6 |
20,4 |
|
7,3 |
14,2 |
1,6 |
4,5 |
6,5 |
16,9 |
4,6 |
9,7 |
5 |
9,9 |
|
7,9 |
16,2 |
1,8 |
4,6 |
9,1 |
36,5 |
7,3 |
18,8 |
4,2 |
8,3 |
|
1,1 |
2,9 |
6,5 |
16,9 |
4,7 |
9,5 |
7,8 |
22,4 |
4,3 |
8,3 |
|
2,2 |
3,7 |
4,9 |
10,4 |
1 |
3,6 |
3,5 |
7,2 |
8,8 |
27,3 |
|
6,1 |
10,4 |
2,2 |
5,3 |
3,6 |
7,1 |
7 |
17,8 |
5,9 |
12,6 |
|
9,3 |
23,4 |
1,5 |
3,9 |
7,2 |
20,8 |
6,5 |
15,6 |
2,4 |
5 |
|
1,7 |
3,4 |
7 |
20,1 |
2,1 |
4 |
4 |
8,6 |
8,8 |
27,1 |
|
6 |
9,7 |
6,5 |
16,6 |
8,5 |
30,5 |
3 |
6,1 |
6,4 |
14,5 |
|
0,6 |
2,4 |
7,7 |
24 |
9,2 |
37,9 |
8,6 |
27,5 |
8,3 |
23,8 |
|
8,7 |
20,2 |
7,6 |
5,4 |
7,3 |
21,6 |
4 |
8,6 |
0,3 |
3,7 |
|
6 |
7 |
8 |
9 |
10 |
|||||
|
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
|
2,4 |
5,8 |
8,5 |
35,7 |
1,2 |
2,7 |
4,8 |
7,2 |
2,4 |
3,7 |
|
4,8 |
10,2 |
0 |
2,4 |
8,6 |
17,3 |
9,9 |
32,2 |
3 |
5,1 |
|
4,5 |
10 |
8,4 |
34,8 |
7,9 |
13,9 |
4 |
6,3 |
8,6 |
21 |
|
6,8 |
18,4 |
9,9 |
54 |
4,9 |
6,7 |
5,9 |
10,3 |
5,7 |
9,6 |
|
9,2 |
34,6 |
6,2 |
17,5 |
1 |
2,9 |
7,1 |
14,9 |
1,7 |
3,1 |
|
2,4 |
5,5 |
3,2 |
7,2 |
7 |
11,5 |
3,5 |
4,8 |
9,4 |
26,9 |
|
7,6 |
22,1 |
0,4 |
3,2 |
9,7 |
22,4 |
4,1 |
6,1 |
5,5 |
9,1 |
|
1,4 |
4,4 |
6,3 |
18,1 |
9,5 |
21,9 |
4 |
6,2 |
9,3 |
26,2 |
|
0,3 |
3 |
8 |
31 |
5,3 |
7,5 |
8,1 |
18,8 |
8,4 |
20,5 |
|
1,1 |
3,8 |
4,1 |
9,6 |
6,7 |
10,8 |
6,9 |
13,9 |
2,8 |
4,4 |
|
3,5 |
7,2 |
5,6 |
14,8 |
7,4 |
12,8 |
6,2 |
11,5 |
9,3 |
25,8 |
|
7,9 |
23,9 |
76 |
27 |
4,5 |
5,9 |
7 |
14,4 |
1,9 |
3,6 |
|
7 |
19,3 |
2,6 |
5,7 |
1,5 |
3,1 |
2,6 |
4,4 |
6 |
10,2 |
|
2,1 |
5,4 |
3,1 |
6,7 |
5,4 |
7,6 |
3,8 |
6 |
7,2 |
14,3 |
|
5,4 |
12 |
7,3 |
25,3 |
0,5 |
2,4 |
4,6 |
6,7 |
5,8 |
9,8 |
|
5,2 |
11,9 |
4,2 |
10,1 |
5,1 |
7,1 |
3,8 |
6,1 |
5,2 |
8,6 |
|
0,9 |
3,7 |
4,4 |
10,5 |
7,4 |
12,8 |
0,7 |
2,6 |
8,7 |
22,1 |
|
8,5 |
28,5 |
6,8 |
21,6 |
2,3 |
3,4 |
4,6 |
6,8 |
7,9 |
17,9 |
|
9,3 |
35,5 |
6,5 |
19,6 |
1,2 |
2,5 |
1,4 |
2,7 |
3,4 |
5,2 |
|
6,3 |
15,4 |
5,6 |
14,9 |
0,5 |
2 |
2,3 |
3,3 |
4,6 |
7,6 |
|
11 |
12 |
13 |
14 |
15 |
|||||
|
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
|
4,3 |
5,9 |
7,3 |
17,7 |
9,4 |
35,6 |
0 |
2,6 |
9,8 |
33,6 |
|
3,4 |
5,3 |
3,6 |
7,4 |
0,5 |
2,7 |
1,4 |
3,5 |
9,9 |
33,7 |
|
9,1 |
23,2 |
7,1 |
17,3 |
2,7 |
5,6 |
2,7 |
4,7 |
9 |
26,9 |
|
1,9 |
3,6 |
4,8 |
9,8 |
2,9 |
6,3 |
7,1 |
15,2 |
0,9 |
3,6 |
|
5,7 |
9,6 |
1 |
4,1 |
2,4 |
5,5 |
1,5 |
3,9 |
4,4 |
7,9 |
|
1,1 |
3 |
8 |
20,9 |
7,4 |
20,2 |
5,9 |
10,9 |
9,7 |
31,9 |
|
5,8 |
9,6 |
0,2 |
2,9 |
7,3 |
20,4 |
0,9 |
3,4 |
5,3 |
9,9 |
|
6,9 |
13,1 |
4,2 |
8,2 |
4,5 |
9,4 |
0,8 |
2,6 |
1 |
3,4 |
|
3,8 |
5,2 |
4,9 |
9,9 |
4,1 |
8,6 |
9 |
24,7 |
4,8 |
8,6 |
|
0,6 |
2,1 |
6,1 |
13,7 |
5,1 |
11,3 |
5,9 |
10,8 |
3,4 |
5,9 |
|
2,7 |
4,1 |
0 |
2,4 |
3,1 |
5,9 |
3,2 |
5,2 |
0,3 |
2,9 |
|
1 |
2,2 |
9,9 |
34,3 |
2,8 |
5,7 |
8,2 |
20 |
6 |
12,2 |
|
2,6 |
4 |
3,7 |
7,7 |
6,3 |
15,6 |
8,2 |
19,8 |
7,4 |
18,1 |
|
8,7 |
20,8 |
0,1 |
2,6 |
7,9 |
23,3 |
2,4 |
4,4 |
8,7 |
25 |
|
1 |
2,6 |
8,1 |
22,1 |
8,6 |
28,5 |
7,2 |
15,4 |
4,9 |
8,7 |
|
3,5 |
5 |
6,7 |
15,4 |
4,8 |
10,2 |
7,7 |
18,1 |
3,7 |
6,7 |
|
6,5 |
11,9 |
2,3 |
5,1 |
0,6 |
3,5 |
4,8 |
8,3 |
3,8 |
7 |
|
3,6 |
4,9 |
4 |
7,7 |
1,5 |
3,7 |
7,5 |
17 |
0,1 |
2,5 |
|
4,3 |
6,6 |
8,8 |
26 |
4,9 |
10,7 |
3,1 |
5,7 |
7,6 |
18,6 |
|
7,8 |
16,1 |
3,6 |
7,2 |
1,3 |
3,8 |
1,5 |
4,1 |
1 |
2,8 |
