ПРАКТИЧНЕ
ЗАНЯТТЯ №9
Тема: Статистика
банківської діяльності
План практичного заняття
1. Сутність
відсотків і відсоткових ставок.
2. Нарощення за
простими відсотками.
3.Дисконтування та
облік за простими відсотками.
4. Визначення
тривалості позички і рівня відсоткових ставок.
5. Нарахування
складних річних відсотків.
6. Номінальна та
ефективна ставки відсотків.
7. Облік
(дисконтування) за складною ставкою відсотків.
8. Операції зі
складною обліковою ставкою.
9. Порівняння
процесів нарощення за різними відсотковими ставками.
10.Визначення строку
платежу і рівня відсоткових ставок.
Термінологічний словник ключових понять
Відсотки — це плата за користування позиченими грошима або
абсолютна величина доходу від наданих у борг грошей у будь-якій формі.
Відсоткова ставка — це відношення відсотків або суми
відсоткових грошей, виплачених за певний періоду часу (рік, місяць), до величини
позички (суми боргу).
Ефективна ставка відсотків — річна ставка складних відсотків, еквівалентна
номінальній ставці при нарахуванні відсотків m разів на рік. Вона показує
реальний відносний дохід, який отримують у цілому за рік.
Капіталізація відсотків — це процес нарахування складних
відсотків і додавання їх до суми, яка служила базою для їх нарахування.
Номінальна ставка відсотків — це річна сумарна ставка відсотків j
при m нарахуваннях відсотків на рік.
Облікова ставка відсотків (позначається d) — це ставка, яка використовується
при нарахуванні і збиранні відсотків наперед (перед початком терміну
користування грошима). Сума, яка видається позичальнику, менша від кінцевої
суми боргу на величину відсоткових грошей, нарахованих за обліковою ставкою.
Складні відсотки — це відсоткові гроші, при нарахуванні
яких за базу приймається нарощена сума попереднього періоду.
Ставка відсотків (позначається і) — це ставка, яка
використовується при нарахуванні відсоткових грошей від початкової суми боргу з
нарахованими за попередні періоди відсотками.
Розв’язок типових задач
1. Видано кредит у
сумі 1000 грн на строк 2 роки під 5 % річних. Необхідно визначити відсоток,
який отримує кредитор, та суму, яку боржник виплатить наприкінці строку.
Розв’язання:
Спочатку визначимо
величину відсотка:
I = P × i × n =1000 × 0,05 × 2 =100 грн,
а потім нарощену суму:
S = P +1 = 1000 +100 = 1100 грн.
Цю задачу можна розв’язати й іншим
способом:
S = P (1 + n × i) =1000 (1 + 2 × 0,05) =1100;
I = S – P = 1100 –1000 = 100 грн.
2. Якою буде
нарощена сума позички, якщо в угоді передбачається за перші два роки
нарахування 10 % річних, а в наступні два роки ставка простих відсотків
збільшується кожні півроку на 1 п. п. Початкова сума позички дорівнювала 1000
грн.
Розв’язання:
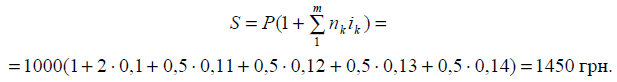
3. Необхідно визначити, яку суму
видасть кредитор, і суму дисконту, якщо через три місяці з моменту видачі
кредиту боржник сплатить кредитору 1025 грн. Кредит надано під 10 % річних.
Розв’язання:
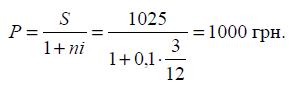
Величина дисконту D = S – P = 1025 – 1000 = 25 грн.
4. Необхідно знайти
при обліку векселів суму, яку банк виплатить власнику, якщо останній врахував
вексель у банку 15 жовтня. Вексель був наданий на суму 1000 грн. з оплатою 15
листопада. Облікова ставка — 10 %.
Розв’язання:
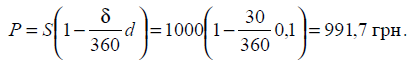
5. Визначити, яку облікову ставку
застосував банк, заплативши 1240 грн. під час обліку векселя, викупна ціна
якого становить 1300 грн. Термін платежу за векселем через 4 місяці.
Розв’язання:

6. Кредит надано в сумі 1000 грн.
Відсоткова ставка — 10 % річних. Нараховуються прості відсотки. У кінці строку
боржник поверне суму в розмірі 1040 грн. Необхідно визначити, на який строк
буде надано цей кредит.
Розв’язання:
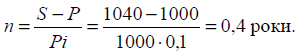
7. Необхідно визначити суму, яку
потрібно поставити в бланку векселя за умови, що строк векселя — 3 місяці,
облікова ставка — 10 %, під вексель надається 1000 грн.
Розв’язання:
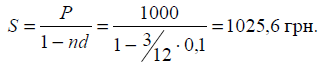
8. Кредит надано в сумі 1000 грн на 5
років за складною ставкою відсотків 10 % річних. Визначити, яку суму повинен
повернути боржник наприкінці строку позички.
Розв’язання:
S = P(1 + i)n = 1000(1 + 0,1)5 = 1610,5
грн.
9. Відсоткова ставка за позичкою
визначена на рівні 8,5 % плюс надбавка 0,5 п. п. в перші два роки та 0,75— у наступні
три роки.
Розв’язання:
Множник наростання у даному випадку
становитиме 1,092 1,09253 = 1,549.
10. Кредит у розмірі 30 тис. грн
надано на строк 3 роки і 160 днів. Якщо обумовлена в контракті ставка дорівнює
6,5 % і передбачено змішаний метод нарахування відсотків, то сума боргу на
кінець строку становитиме:
Розв’язання:
S = 30 000 ×1,0653
× (1+160/365 0,065) = 37 271 грн.
За формулою наростання складних
відсотків:
S = 30 000 ×1,0653
×1,065160/365 = 37 252 грн.
11. Кредит надано в розмірі 1000 грн
на 5 років під 12 % річних. Відсотки на суму боргу нараховуються щомісячно.
Необхідно визначити величину боргу наприкінці строку позички.
Розв’язання:
S = P(1+ j/m)mn =1000(1+ 0,12 /12)12×5
=1816,7 грн.
12. Номінальна ставка — 6 % річних,
відсотки нараховуються кожні півроку. Визначити ефективність цього процесу
нарощення.
Розв’язання:
i = (1+ j/m)m –1 =1,032 –1 =
6,09%.
Це означає, що позичка, яка надана
під 6 % річних за умови, що відсотки нараховуються двічі на рік, принесе
кредитору відносний дохід у розмірі 6,09 % на рік. Заміна в договорі номінальної
ставки j при нарахуванні відсотків m разів на рік на ефективну ставку i не
змінює фінансових зобов’язань сторін, які беруть участь у договорі, тобто
учасникам фінансової угоди байдуже, яку використовувати ставку: 6,09 % при
нарахуванні відсотків один раз на рік або 6 % при нарахуванні відсотків два
рази на рік.
13. Необхідно визначити, яку суму
треба покласти на рахунок у банк, який нараховує 10 % річних за складною
ставкою відсотків, щоб через 5 років отримати суму в 1000 грн.
Розв’язання:
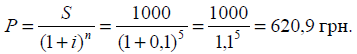
14. В умовах випуску сертифікатів
(номіналом 1000 грн) були передбачені викупні суми, які залежать від строку
зберігання: при п’ятирічному виплачувалось 1415 грн, десятирічному 2595 грн.
Які значення мають річні складні ставки відсотків, котрі дають таке наростання?
Розв’язання:
i = (S/P)1/n–
1 = (1415/1000)1/5 – 1 = 0,07189;
i = (2595/1000)1/10 – 1 =
0,1.
15. Вексель виписано на строк 2 роки.
Якою повинна бути складна облікова ставка, щоб при обміні векселя власник отримав
90 % його суми?
Розв’язання:
![]()
16. Кредит надано у сумі 1000 грн за
ставкою складних відсотків 10 % річних. Боржник повинен у кінці строку позички
повернути 1200 грн. Необхідно визначити, на який строк було надано кредит.
Розв’язання:
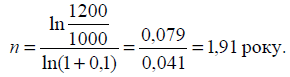
17. Чому дорівнюватиме
сума в 1000 грн через 10 років за умови, що на цю суму нараховуються 6 %
річних? Якою буде її реальна купівельна спроможність, якщо приріст цін в
середньому дорівнюватиме 3 % (перший варіант) і 8 % (другий варіант)?
Розв’язання:
S = 1000 × 1,0610 = 1790,8.
Перший варіант 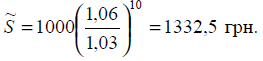
Другий варіант 
Навчальні задачі
Завдання 1. Визначити відсотки і суму
накопиченого боргу, якщо сума виданих грошей — 5000 грн, строк позички — 2
роки, ставка відсотків — 5 %.
Завдання 2. Обсяг позички — 100 000 грн,
строк позички — з 1 березня по 6 жовтня поточного року. Відсоткова ставка — 6
%. Визначити трьома можливими способами суму накопиченого боргу і відсоток.
Завдання 3. Існують два варіанти
кредитування. Первісний розмір позички в обох випадках — 14 000 грн. При
першому варіанті тривалість позички — 65 днів, відсоткова ставка — 6,5 %
річних. При другому варіанті тривалість позички — 72 дні, а облікова ставка —
5,8 %. Визначити, який варіант найвигідніший для боржника.
Завдання 4. Якою буде відсоткова сума
позички, якщо в контракті передбачено за перші два роки нараховувати по 10 %
річних, у наступні два роки — по 12 %, а в останні три роки ставка відсотків підвищуватиметься
в кожному півріччі на 0,5 пункти? Сума позички дорівнює 1000 грн.
Завдання 5. Визначити відсотки, якщо
позичка була надана в розмірі 200 грн. Строк позички — 6 місяців. Ставка
відсотків — 2 %.
Завдання 6. Позичка видана в розмірі 100
грн під 6 % річних. Сторони домовились, що через деякий час боржник поверне
кредитору суму в розмірі 150 грн. Визначити, через який строк він повинен повернути
свій борг.
Завдання 7. Зобов’язання сплатити через
160 днів 30 грн з відсотками (5 % річних) було враховане за 100 днів до
настання строку, облікова ставка — 6 %. Визначити отриману суму.
Завдання 8. Сторони домовились про те, що
із суми кредиту, виданого на 210 днів, відраховується дисконт у розмірі 12 %.
Необхідно визначити ціну кредиту у вигляді простої облікової ставки.
Завдання 9. Первісна сума боргу — 100
грн. Строк позички — 3 роки. Ставка відсотків — 8 %. Відсотки капіталізуються 4
рази на рік. Визначити величину відсотка.
Завдання 10. Визначити очікувану величину
компенсації, якщо передбачається видати позичку в розмірі 100 грн на строк 3
роки при ставці 2 % річних, а передбачуваний темп інфляції — 3 %.
Завдання 11. Зобов’язання у сумі 500 грн.
повинно бути погашено через 4 роки, облікова ставка 12 %. Нарахування дисконту
щоквартальне. Знайти розмір дисконту.
Завдання 12. Позичка видана в розмірі 100
грн під 6 % річних. Сторони домовились, що через деякий час боржник поверне
кредиторові суму в розмірі 150 грн. Визначити, через який строк боржник повинен
повернути гроші.
Завдання 13. Визначити, яку величину має
становити номінальна ставка відсотків, якщо сума позички повинна подвоїтися за
4 роки, а відсотки нараховуються за кожні півроку.
Завдання 14. Визначити реальну суму
відсотків, якщо первісна сума боргу дорівнює 100 грн, строк — 3 роки,
відсоткова ставка — 3 %, а темп інфляції — 2 % на рік.
Завдання 15. Зобов’язання, що дорівнює 1000 грн,
повинно бути погашено через 5 років, облікова ставка — 5 %, нарахування поквартальне.
Знайти сучасну величину зобов’язання, розмір дисконту, ефективну облікову
ставку.
Завдання 16. Первісна сума боргу становить 4500 грн.
Строк позички — 2 роки. Відсотки капіталізуються щомісячно. Номінальна ставка відсотків
— 0,08. Визначити відсоток та еквівалентну номінальній ефективну ставку
відсотків.
Завдання 17. Позичка в 1500 грн надана на строк 4
роки за номінальною ставкою 6 % річних. Відсотки капіталізуються поквартально. Якщо
протягом перших 4 років позичка не виплачується, то номінальна ставка
підвищується на 3 п. п. Строк погашення — 6 років. Визначити суму накопиченого
боргу і відсоток.
Завдання для перевірки знань
1. Що таке нарощення боргу та як його
обчислити?
2. Які існують види відсоткових
ставок?
3. У чому полягає різниця між ставкою
відсотків та обліковою ставкою?
4. Яка ставка називається простою
відсотковою ставкою?
5. Від чого залежить розмір
відсоткових грошей?
6. Що ви розумієте під принципом
нерівноцінності грошей:
а) гроші втрачають свою вартість з
часом внаслідок інфляційних процесів;
б) будь-яка сума грошей
теоретично може бути інвестована;
в) теоретично будь-яка сума грошей
може бути інвестована і принести дохід;
г) усе викладене.
7. Які бувають відсоткові ставки за
методом нарахування відсотків:
а) фіксовані і плаваючі (змінювані);
б) складні і прості;
в) постійні і змінювані;
г) ставка відсотків та облікова
ставка.
8. Якщо ставка відсотків
застосовується до однієї початкової суми і протягом усього строку, то це:
а) складні відсоткові ставки;
б) фіксовані ставки;
в) прості відсоткові ставки;
г) змінні прості відсоткові ставки.
9. Що ви розумієте під нарощеною
сумою позички:
а) нараховані відсотки за користування
позичкою;
б) приєднання відсотків до суми, яка
повинна бути виплачена в кінці строку позички;
в) первісна сума
позички разом з нарахованими відсотками до кінця строку;
г) вірної відповіді
немає.
10. Які з
нижченаведених висловлювань є визначенням відсотків:
а) абсолютна
величина доходу від надання грошей у борг у будьякій формі;
б) відношення
відсоткових грошей, виплачуваних за фіксований відрізок часу, до величини
позички;
в) відносна величина
доходу від наданих грошей в борг у будь-якій формі;
г) абсолютний дохід
від надання грошової позички.
11. Які з наведених
нижче формул є множниками нарощення:
а) (1 + ni); б) (1 – nd); в) (1 + ni)-1;
г) всі формули.
12. Що вимірюють
ефективні ставки відсотків?
а) реальний
відносний дохід, який отримають в цілому за рік;
б) реальний
абсолютний дохід, який отримають в цілому за рік;
в) дохід від
вкладених коштів, який визначається за річною ставкою відсотків;
г) нічого з
вищевикладеного.
13. Які з наведених
співвідношень неправильні:
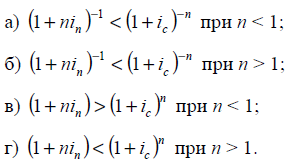
14. Яка з наведених
формул є формулою подвоєння за простими відсотками:
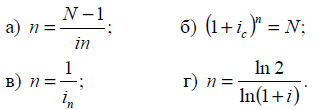
15. Яка з наведених
формул є дисконтним множником:
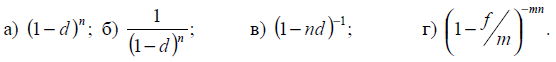
16. Яка з наведених
формул лежить в основі змішаного методу на-
рахування відсотків:
а) S = P(1 + i)n (1 + ni);
б) S = P(1 + ai) (1 + bi);
в) S = P(1 + i)a (1 + bi);
г) S = P(1 + i)n (1 + bi).
17. В якій з
наведених формул є помилка:
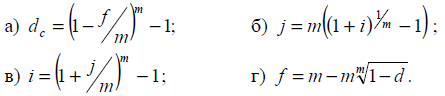
18. Що таке складні
відсотки?
19. У чому полягає
суть капіталізації відсотків?
20. Чому нарахування
складних відсотків при довготермінових фінансово-кредитних операціях вигідніше
кредитору, ніж нарахування простих відсотків?
21. Яка ставка
називається номінальною?
22. Для чого використовується ефективна ставка відсотків?

