Тема: Характеристика
вищих фінансових обчислень
План практичного заняття
1. Поняття і види фінансових рент.
2. Нарощена сума звичайної ренти.
3. Сучасна величина звичайної ренти.
4. Визначення
параметрів фінансової ренти.
Термінологічний словник ключових понять
Вічна рента — це послідовність необмеженої
кількості платежів, які сплачуються протягом нескінченого числа років.
Нарощена сума ренти — сума всіх членів ренти з
нарахованими на них відсотками на кінець її строку.
Сучасна величина ренти — сума всіх її членів,
дисконтованих на початок її строку.
Фінансова рента (ануїтет) — це послідовність платежів,
які сплачуються у вигляді грошової суми через рівні проміжки часу, незалежно від
їх походження, мети та використання.
Розв’язок типових задач
1. Визначити суму, яка буде в кінці
п’ятирічного періоду на рахунку в банку, якщо на депозит у кінці кожного
періоду вносять по 200 грн. Банк нараховує відсотки за ставкою 10 % річних.
Розв’язання:
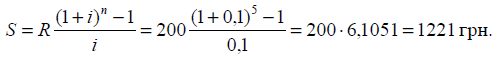
2. Знайти нарощену суму ренти за
умови, що відсотки нараховуються щоквартально. Внески робляться протягом 5
років наприкінці року по 20 тис. грн. На зібрані кошти нараховуються відсотки
за ставкою 12 % річних:
Розв’язання:
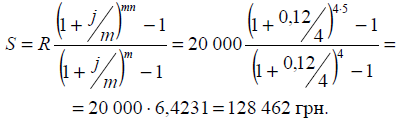
3. Визначити суму,
яка буде в кінці п’ятирічного періоду на рахунку в банку, якщо на депозит у
кінці кожного місяця робляться внески. Загальна сума надходжень протягом року становить
200 грн. Банк нараховує відсотки за ставкою 10 % річних.
Розв’язання:
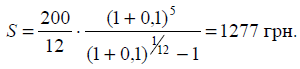
4. На рахунок банку
щомісячно робляться внески по 100 грн. Банк нараховує 12 % річних за ставкою
складних відсотків. Необхідно знайти суму, яка буде нагромаджена на рахунку
через 5 років, якщо банк нараховує відсотки щоквартально.
Розв’язання:
У такому разі річна
сума внесків дорівнюватиме 1200 грн, тобто R = 1200.
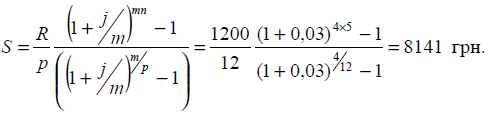
5. Необхідно
визначити суму, котру треба внести на рахунок у банку, який нараховує відсотки
в кінці року за ставкою складних відсотків у розмірі 5 % річних, для того, щоб
виплачувати протягом 5 років у кінці року додаткову пенсію в сумі 100 грн.
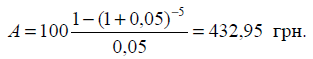
6. Необхідно
визначити суму, яка потрібна для того, щоб можна було виплачувати кредиторові
щоквартально 100 грн. протягом 5 років, якщо на ваш рахунок у банку відсотки
нараховуються кожні півроку за складною ставкою відсотків 5 % річних.
Розв’язання:
Член ренти R = 100 × 4 = 400;
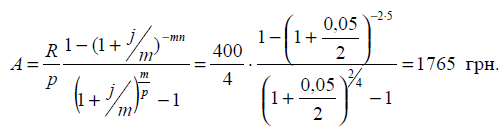
7. Скільки коштує
акція з щорічними дивідендами 40 грн, якщо відсоткова ставка, за якою
дисконтуються подібні акції, дорівнює 8 %.
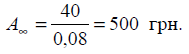
Отже, вартість даної
акції 500 грн.
8. У кінці
п’ятирічного строку необхідно погасити заборгованість у сумі 10 000 грн шляхом
створення фонду на депозитному рахунку в банку. Банк нараховує 10 % річних.
Необхідно визначити величину рівних щорічних внесків для створення цього фонду.
Розв’язання:
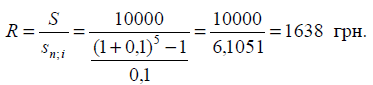
З іншого боку,
виникає задача погашення поточного боргу в сумі 10 000 грн шляхом щорічних
виплат кредиту. Кредит було надано під 10 % річних на п’ять років. Задача
полягає у визначенні розміру щорічних виплат:
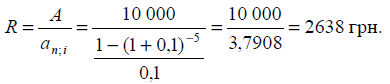
9. Припустімо, що
куплено пакет акцій на 10 000 грн і дивіденди виплачуватимуться у кінці року в
розмірі 1000 грн. За який строк окупляться суми, витрачені на купівлю акцій,
якщо їх можна було б покласти на рахунок у банку під 5 % річних.
Розв’язання:
Окупність матиме
місце тоді, коли сучасна величина дивідендів дорівнює сумі, що була витрачена
для купівлі акцій:

Таким чином,
вкладення в акції окупляться через 14,2 року за умови, що дивіденди
виплачуватимуться регулярно і відсоткові ставки на фінансових ринках не
змінюються.
11. Вартість партії
товарів 100 тис. грн, які сплачуються протягом трьох років. Кредит надається
під 10 % річних, платежі вносяться кожні півроку. Покупцеві надана відстрочка
на три місяці, при цьому відсотки за час відстрочки приєднуються до вартості
товарів. Яким чином здійснюватиметься погашення кредиту?
Розв’язання:
Спочатку необхідно
визначити вартість товарів на кінець відстрочки:
![]()
Ця сучасна величина
повинна бути сплачена за три роки.
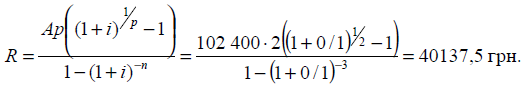
Навчальні задачі
Завдання 1. У кінці кожного кварталу на рахунок до
банку перераховується сума грошей. Річна сума внесків 100 грн, і на ці кошти нараховуються
8 % річних. Знайти нарощену суму ренти через 10 років за умови, що відсотки на
кошти на рахунку нараховуються щоквартально.
Завдання 2. Необхідно визначити суму, яка потрібна
для того, щоб можна було виплачувати кредитору кожні півроку 50 грн протягом 2 років,
якщо на ваш рахунок у банку відсотки нараховуються щомісячно за річною ставкою
12 %.
Завдання 3. Необхідно знайти нарощену суму ренти
за умови, що відсотки нараховуються кожні півроку. Строк ренти — 10 років. Виплата
платежів один раз на кінець року по 100 грн. Ставка, за якою нараховуються
відсотки на платежі, дорівнює 10 %.
Завдання 4. Строк ренти 2 роки. Річна сума ренти
становить 100 грн. Нарахування відсотків щомісячне, за ставкою 12 % річних.
Знайти сучасну величину ренти.
Завдання 5. Рента виплачується два рази на рік.
Річна сума ренти — 100 грн. Рента виплачуватиметься протягом двох років.
Нарахування відсотків щомісячне, за ставкою 12 %. Визначити нарощену суму ренти.
Завдання 6. Визначити величину рівних внесків,
якщо необхідно до кінця десятирічного періоду створити фонд, який дорівнюватиме
100 000 грн. Ставка відсотків — 10 %.
Завдання 7. Строк ренти 10 років. Виплата платежів
— один раз наприкінці року по 100 грн. Ставка, за якою нараховуються відсотки по
платежах, — 10 %. Визначити накопичену суму ренти.
Завдання 8. Строк ренти 5 років. Нарахування
відсотків у кінці року — за ставкою 5 %. Член ренти дорівнює 100 грн. Знайти
сучасну величину ренти.
Завдання 9. Визначити величину щомісячних внесків
на спеціальний рахунок у банку для погашення поточної заборгованості в розмірі 100
000 грн. Її необхідно погасити протягом двох років. Ставка відсотків — 12 %.
Відсотки нараховуються щомісячно.
Завдання 10. Строк ренти 10 років. Виплата платежів
— один раз наприкінці року по 100 грн. Ставка, за якою нараховуються відсотки
по платежах — 10 %. Визначити накопичену суму ренти.
Завдання 11. Строк ренти 5 років. Нарахування
відсотків у кінці року за ставкою 5 %. Член ренти дорівнює 100 грн. Знайти
сучасну величину ренти.
Завдання для перевірки знань
1. Що ви розумієте під таким
визначенням: «Множину розподілених у часі платежів називають…»—
а) фінансовою рентою;
б) ануїтетом;
в) потоком платежів;
г) усим викладеним.
2. Яка з
наведених формул є формулою нарощеної суми ренти:


3. Що ви розумієте під таким
визначенням: «Сума всіх членів послідовності платежів з нарахованими на них
відсотками на кінець його строку» —
а) капіталізовану величину ренти;
б) нарощену суму ренти;
в) сучасну величину ренти;
г) приведену величину ренти.
4. Які з викладених нижче
висловлювань неправильні:
а) член ренти — величина кожного
окремого платежу;
б) відсоткова ставка — ставка, яка
застосовується при нарощуванні або дисконтуванні платежів, з яких складається
рента;
в) період ренти — час, який
вимірюється від початку фінансової ренти до кінця останнього її періоду;
г) потік платежів — це множина
розподілених у часі платежів.
5. Яка з викладених нижче формул є
сучасною величиною
ренти:

6. Під рентою розуміють:
а) множину розподілених у часі
платежів;
б) потік платежів, усі члени якого
позитивні величини, а часові інтервали між двома послідовними платежами —
постійні;
в) потік платежів, усі члени якого
позитивні величини незалежно від походження цих платежів, їх призначення і
цілей;
г) множина розподілених у часі як
позитивних, так і негативних платежів.
7. Що таке фінансова рента?
8. Якими параметрами описується
фінансова рента?
9. Що таке нарощена сума ренти?
10. Дайте
визначення сучасної величини ренти.

