2.4.   Переведення чисел з однієї системи і іншу

 

Для переведення чисел із будь-якої системи числення в десяткову необхідно це число представити у вигляді полінома і розкрити всі члени полінома в десятковій системі числення.

Наприклад:

з шістнадцяткової в десяткову:

92C8₁₆ = 9*10₁₆³ + 2*10₁₆² + C*10₁₆¹ + 8*10₁₆⁰ = 9*16₁₀³ + 2*16₁₀² + 12*16₁₀¹ + +8*16₁₀⁰ = 37576

з вісімкової в десяткову:

735₈ = 7*10₈²  + 3*10₈¹ + 5*10₈⁰  = 7*8₁₀² + 3*8₁₀¹ + 5*8₁₀⁰ = 477₁₀

(24,3)₈  = 2*8¹ + 4*8⁰ + 3*8^-1 = 16 +4 +3/8 = (20,6373)₁₀

з двійкової в десяткову:

110100101₂=1*10₂⁸+1*10₂⁷+0*10₂⁶+1*10₂⁵+0*10₂⁴+0*10₂³+1*10₂²+0*10₂¹+1*10₂⁰=1*2₁₀⁸+1*2₁₀⁷+0*2₁₀⁶+1*2₁₀⁵+0*2₁₀⁴+0*2₁₀³+1*2₁₀²+0*2₁₀¹+ 1*2₁₀⁰ = 421₁₀

 

Переведення цілого числа з десяткової системи у будь-яку іншу здійснюється шляхом послідовного ділення числа на основу нової системи числення. Ділення виконується до тих пір, поки остання частка не стане меншою дільника. Отримані остачі від ділення взяті у зворотному порядку, будуть утворювати число в новій системі числення.

Завдання: перевести число 999 з десяткової системи числення в двійкову

(999)₁₀ = ( ? ) ₂

Приклад виконання завдання

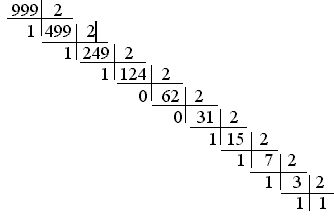
Отже, (999)10 =  (1111100111)2