Тема 14-15. Функціональні пристрої комп'ютерної
(цифрової) електроніки
Логічні
пристрої, вихідні сигнали яких однозначно визначаються комбінацією вхідних
логічних змінних у розглянутий момент часу, називаються комбінаційними.
У процесі
проектування будь-якого пристрою виконується ряд дій, які можна віднести до
завдань аналізу та синтезу.
Виконання
завдань аналізу КЦП припускає наявність готової функціональної схеми пристрою
на логічних елементах заданого базису. У процесі аналізу оцінюються деякі
характеристики наявної схеми КЦП. Наприклад, можна скласти булевий вираз і
таблицю істинності, що визначають перетворення інформації в КЦП; мінімізувати
логічну функцію, яку виконує аналізована схема; оцінити апаратні витрати на
реалізацію схеми; її швидкодію; споживану потужність; розглянути можливість
утворення в схемі помилкових небезпечних станів в результаті змагань (гонок) та
ін.
Синтез
КЦП передбачає побудову функціональної схеми пристрою, тобто визначення складу
необхідних логічних елементів і з'єднань між ними, при яких забезпечується
перетворення вхідних цифрових сигналів у вихідні відповідно до заданих умовами
роботи пристрою [7,8]. У процесі синтезу необхідно мінімізувати апаратні
витрати на реалізацію пристрою. Розглянемо особливості синтезу КЦП з одним
виходом. Послідовність синтезу доцільно розбити на ряд етапів.
Етап 1.
Завдання логічної функції, що визначає функціонування синтезованого КЦУ. Як
зазначалося раніше, це можна зробити словесно, за допомогою таблиць істинності
чи булевих виразів.
Етап 2.
Мінімізація логічної функції, яка здійснюється алгебраїчним або графічним
методом (за допомогою діаграм Вейча, карт Карно).
Етап 3.
Запис булевого виразу мінімізованої перемикальної функції.
Етап 4.
Перетворення булевого виразу мінімізованої ПФ для реалізації її в заданому
базисі І-НЕ або АБО-НЕ.
Етап 5.
Складання функціональної схеми КЦУ, тобто зображення потрібних логічних
елементів і зв'язків між ними.
Проілюструємо
етапи синтезу КЦУ на прикладі.
Необхідно
синтезувати на елементах І-НЕ КЦП на три входи, вихідний сигнал яких збігається
з більшістю вхідних сигналів.
Дане
словесний опис задає логічну функцію мажоритарною. Її роботу відображає таблиця
істинності (таблиця 10.1).
Таблиця
10.1 – Таблиця істинності
|
№ набору |
С |
В |
А |
F |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
0 |
|
5 |
1 |
0 |
1 |
1 |
|
6 |
1 |
1 |
0 |
1 |
|
7 |
1 |
1 |
1 |
1 |
Булевий
вираз БФ в СДНФ має такий вигляд:
![]() (10.1)
(10.1)
Мінімізуючи
даний вираз, використовуючи тотожності і теореми булевої алгебри, отримаємо:
![]() (10.2)
(10.2)
Перетворимо
даний вираз для його реалізації в базисі І - НЕ.
Застосовуючи
теорему де Моргана, отримаємо:
![]() (10.3)
(10.3)
Функціональна
схема синтезованого КЦП, що реалізує вираз (10.3) на елементах І-НЕ (рисунок
10.1).

Рисунок
10.1 – Функціональна схема синтезованого КЦП
На
практиці широко застосовуються КЦП, що мають кілька виходів. При проектуванні
таких пристроїв можна скористатися розглянутими вище правилами синтезу, якщо
уявити пристрій у вигляді сукупності відповідного числа КЦП із загальними
входами.
Функціонування
КЦП з m-виходами описується
(задається) аналогічною кількістю, переключаючи функцї, над кожною з яких в
процесі синтезу виконуються дії, описані вище.
У
цифровій техніці при побудові складних пристроїв широко застосовуються не
тільки окремі логічні елементи, що реалізують елементарні булеві функції, але і
їх комбінації у вигляді типових структур, розглядаючих як єдине ціле у вигляді
інтегральних мікросхем (ІМС). На входи таких структур можуть подаватися
інформаційні логічні сигнали і сигнали управління. Останні можуть визначати,
наприклад, порядок передачі інформаційних вхідних сигналів на вихід або
відігравати роль сигналів синхронізації. У багатьох випадках, особливо при
використанні в пристроях вихідних ланцюгів з трьома станами, в якості сигналів
синхронізації виступають сигнали "Вибір мікросхеми" (CS). Наявність
активного значення такого сигналу управління (в одних схемах – це логічний
нуль, в інших—логічна одиниця) дає
змогу пристрою виконувати задані функцій, відсутність же його — переводить
схему в "невибране" стан, при якому вона не обробляє інформацію, а її виходи відключені
від навантаження.
10.2.1. Шифратори і дешифратори
У
повсякденному житті для подання чисел ми застосовуємо десяткову систему
числення [2]. Якщо вона використовується для представлення дискретних
повідомлень (дискретної інформації - даних), то говорять про кодування -
встановлення відповідності між елементами даних і сукупністю символів, названих
кодовою комбінацією. У більшості сучасних комп'ютеризованих систем управління і
автоматики вхідна дискретна інформація представлена у десятковому (унітарному)
коді, а обробка інформації цифровим комп'ютером здійснюється над даними,
представленими в двійковому коді. Виникає завдання перетворення десяткового
(унітарного) коду в двійковий при введенні в систему і зворотного перекладу
двійкового коду в десятковий (унітарний) при виведенні з цифрової системи
результатів обробки інформації.
Комбінаційний
цифровий пристрій (КЦП), що виконує переклад десяткового (унітарного) коду в
двійковий, називається шифратором (кодером) двійкового коду. Перетворення ж
двійкового коду в десятковий (унітарний) здійснює дешифратор (декодер)
двійкового коду.
Дуже
часто десяткові коди перетворяться в двійкові-десяткові, які називають BCD
(Binary Code Decimal) — код або
кодами 8421. У цьому випадку КЦП, перетворюючі десятковий код в BCD-код і,
навпаки, називають відповідно шифратором (кодером) і дешифратором (декодером)
двійково-десяткового коду (BCD-коду).
Поширеним
вихідним пристроєм, що відображає десяткові числа, є семисегментний індикатор.
Його роботою керує дешифратор, який перетворює BCD-код в семисегментний.
Розглянемо названі пристрої більш докладно.
10.2.1.1. Шифратори двійкового коду
Шифратори
двійкового коду перетворять десятковий (унітарний) код в двійковий. Якщо число
розрядів вихідного ДК (виходів шифратора) одне m, то максимальне число вхідних
шин визначається числом можливих кодових комбінацій ДК і становить 2m.
Умовне
позначення шифратора (рисунок 10.2).
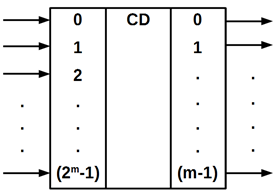
Рисунок
10.2 – Умовне позначення шифратора
На
вихідних шинах встановлюється ДК, десятковий еквівалент якого відповідає номеру
входу, на якому з'явилася логічна 1. На інших входах при цьому присутні нулі.
Такий код називають унітарноим (десятковим).
Розглянемо
приклад проектування шифратора, у якого число розрядів вихідного ДК ![]() .
Максимальне число входів одне
.
Максимальне число входів одне ![]() , що дозволяє відобразити дворозрядним вихідним
двійковим кодом чотирьохдесяткові цифри 0, 1, 2, 3. Іноді при проектуванні
шифраторів нульовій вхід опускають, вважаючи, що нульовий цифрі на вході
відповідають пасивні сигнали (нулі) на всіх залишившихся входах. Активний
вхідний сигнал – логічна 1. Приймаючи такий підхід, складемо таблицю істинності
розглянутого в прикладі (рисунок 10.3) шифратора (таблиця 10.2).
, що дозволяє відобразити дворозрядним вихідним
двійковим кодом чотирьохдесяткові цифри 0, 1, 2, 3. Іноді при проектуванні
шифраторів нульовій вхід опускають, вважаючи, що нульовий цифрі на вході
відповідають пасивні сигнали (нулі) на всіх залишившихся входах. Активний
вхідний сигнал – логічна 1. Приймаючи такий підхід, складемо таблицю істинності
розглянутого в прикладі (рисунок 10.3) шифратора (таблиця 10.2).
Таблиця
10.2 – Таблиця істинності для шифратора
|
№ набора |
С |
В |
А |
F2 |
F1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
|
2 |
0 |
1 |
0 |
1 |
0 |
|
3 |
0 |
1 |
1 |
– |
– |
|
4 |
1 |
0 |
0 |
1 |
1 |
|
5 |
1 |
0 |
1 |
– |
– |
|
6 |
1 |
1 |
0 |
– |
– |
|
7 |
1 |
1 |
1 |
– |
– |
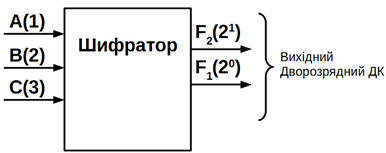
Рисунок
10.3 – Функціональна схема проектованого шифратора
Якщо
провести мінімізацію по не нульовим значенням функцій F2, F1, —отримаємо мінімальні
КНФ:
![]() (10.4)
(10.4)
Мінімізуємо
функції F2, F1 за допомогою діаграм Вейча (рисунок 10.4):
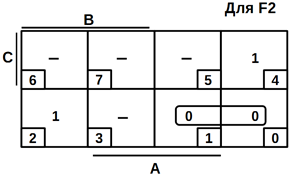
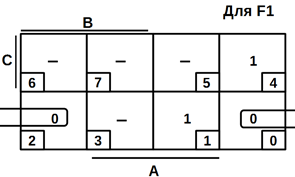
Рисунок
10.4 – Мінімізація логічних функцій
У результуючі кон'юнкції входять ті змінні, які в межах накриття не міняють
свого значення (входять у прямій або інверсній формах). Змінні, які знаходяться
в стовпцях і рядках, не помічених рискою, входять в прямій формі, а помічені -
в інверсній.
Принципова схема шифратора, що реалізує ці рівняння, показана на рисунку
10.5.
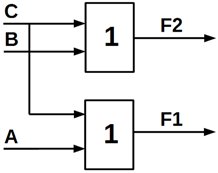
Рисунок 10.5 – Принципова схема шифратора
У цифровій електроніці існує багато ІМС, що виконують функцію шифратора,
наприклад, К555ІВ1. Нижче показані її функціональне значення (рисунок 10.6) і
таблиця істинності (таблиця 10.3).
Кодований сигнал низького рівня (логічний 0) надходить на один з входів X0
... Х7. На інших входах повинні бути сигнали високого рівня (таблиця 10.3).
Мікросхема має керуючий (Стробесення) вхід V і два додаткові виходи: Р—дозвіл перенесення і G - заборона
перенесення. Активними сигналами на цих виходах є логічні одиниці. Сигнали на
вході V дозволяють ІМС працювати в
режимі кодування (V = 0) або
забороняють роботу (V = 1). У разі
заборони (V = 1) на всіх виходах
встановлюються напруги високого рівня незалежно від сигналів на входах. Сигнал
заборони перенесення (Р = 0) з'являється
тоді, коли на всіх інформаційних входах X0
... Х7 будуть сигнали високого рівня (логічні одиниці). У цьому випадку
з'являється одиниця на виході G.
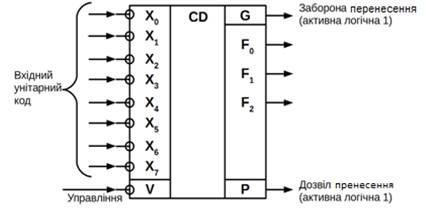
Рисунок 10.6 – Функціональне позначення шифратора
Сигнали з виходів G і P використовують для управління схемою,
яка приймає сигнали з виходів шифратора.
Таблиця 10.3 – Таблиця станів шифратора
|
X7 |
X6 |
X5 |
X4 |
X3 |
X2 |
X1 |
X0 |
F2 |
F1 |
F0 |
G |
P |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
Деякі шифратори основну функцію суміщають з можливістю введення пріоритетів
кодованих сигналів. Мікросхема К555ІВ1 (рисунок 10.5) має таку можливість.
Функція пріоритету реалізується наступним чином. У ІМС допускається одночасне
надходження активних сигналів (логічних нулів) на кілька входів. Пріоритетом
володіє активний сигнал на вході з меншим номером, і вихідний двійковий код
буде відповідати цьому заданому сигналу. Наприклад, при комбінаціях вхідних
сигналів 11110111, 00000111, 10100111, записаних в порядку прийнятому в таблиці
10.3, результат буде один і той же: на виході буде сформований код 011,
оскільки пріоритетом володіє нульовий сигнал на вході Х3.
10.2.1.2. Шифратори двійково-десяткового коду
Шифратори двійково-десяткового коду перетворюють вхідний десятковий
(унітарний) код в двійково-десятковий (BCD) -код (код 8421);. З виходу такого
шифратора паралельно знімається група двійкових сигналів, з яких кожні чотири
(тетрада) відображають у двійковому коді десяткову цифру. Відмінність
чотирирозрядного двійкового коду від чотирирозрядного BCD-коду полягає в
діапазоні зміни комбінацій вихідного коду: у першому випадку вихідний код
змінюється від 0000 до 1111, а в другому – від 0000 до 1001.
В одному байті (восьми бітах) можна упакувати (укласти) дві десяткові цифри
в BCD-код. Такий формат представлення десяткових чисел називається упакованим.
На рисунку 10.6 приведено функціональне позначення шифратора BCD-коду.
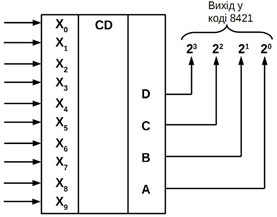
Рисунок 10.7 – Умовне позначення шифратора DCD коду
На вхід системи надходять двійкові цифри від 0 до 9, які відображаються на
виході однієї тетради двійкового коду, яка приймє значення від 0000 В до 1 001
В.
10.2.1.3. Дешифратори двійкового коду
Дешифратором (декодером) двійкового коду називають КЦП, що перетворює
вхідний двійковий код в десятковий (унітарний). Повний дешифратор з m входами
має 2m виходів. Кожній комбінації
вхідних сигналів відповідає активне значення тільки одного певного вихідного
сигналу. Нижче показані таблиця істинності (таблиця 10.4) та умовне позначення
(рисунок 10.8) трьохвходового повного дешифратора з одиничними активними
значеннями вихідних сигналів F0 ... F7.
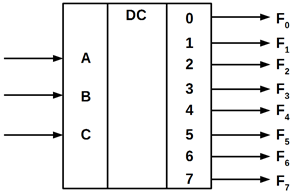
Рисунок 10.8 – Умовне позначення дешифратора
Таблиця 10.4 – Таблиця істинності дешифратора
|
№ набору |
C |
B |
A |
F0 |
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
3 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
4 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
5 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
6 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
7 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
Дешифратор реалізує вісім різних логічних функцій:
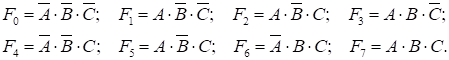 (10.5)
(10.5)
Якщо вхідні змінні розглядати як двійковій запис чисел, то логічна одиниця
формується на тому виході, номер якого відповідає десятковому еквіваленту
вхідного двійкового числа.
Розглянутий дешифратор (таблиця 10.4) є перетворювачем двійкового коду в
унітарний (десятковий).
Наведені булеві вирази функцій F0 ... F7 можна реалізувати на логічних елементах у базисах І, АБО, НЕ;
І-НЕ або АБО-НЕ, користуючись методикою викладеною раніше.
В інтегральному виконанні випускаються різні структури дешифраторів, у яких
є 2, 3 або 4 входи. В одному корпусі може бути декілька дешифраторів.
Для збільшення функціональних можливостей пристроїв часто передбачається
використання декількох додаткових сигналів управління. Як приклад на рисунку
10.9 дане зображення мікросхеми К555ИД4, що містить здвоєний двовходовий
дешифратор з активними нульовими вихідними сигналами.
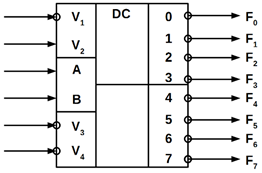
Рисунок 10.9 – Умовне позначення мікросхеми К555ИД4
Вихідні сигнали обох дешифраторів залежать від комбінації вхідних сигналів
А, В. Синхронізація процесу формування вихідних сигналів F0 ... F3
для кожного дешифратора задається комбінаціями керуючих сигналів V. Роботу верхнього дешифратора
забеспечує комбінація V1 =
0, V2 = 1, а роботу
нижнього – V3 = 0, V4 = 0. Введення такого
управління розширює можливості мікросхеми при побудові більш складних
пристроїв, наприклад, дешифраторів зі збільшеним числом входів і виходів.
На рисунку 10.9 показаний приклад
включення двох мікросхем К555ИД4 для реалізації дешифратора чотирирозрядного
вхідного двійкового коду у вихідний шістнадцятипозиційний унітарний
(десятковий) код. Роботу цього дешифратора відображено на таблицях 10.5 і 10.6.
Таблиця 10.5 – Робота дешифратора
|
X3 |
X2 |
Робочий дешифратор |
|
0 |
0 |
Нижній ИМС DD1 |
|
0 |
1 |
Верхній ИМС DD1 |
|
1 |
0 |
Нижній ИМС DD2 |
|
1 |
1 |
Верхній ИМС DD2 |
Таблиця 10.6 – Робота дешифратора
|
№ набору |
X3 |
X2 |
X1 |
X0 |
F0 |
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 |
F11 |
F12 |
F13 |
F14 |
F15 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
2 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
3 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
4 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
5 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
6 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
7 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
8 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
9 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
10 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
11 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
12 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
13 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
14 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
|
15 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
Дешифратори можуть бути неповними (мають число виходів ![]() , де
, де
m – число вхідних змінних).
Наприклад, такі дешифратори можуть використовуватися для перетворення
двійково-десяткового коду в код, призначений для управління десятковим
індикатором (дешифратори 4х10). На рисунку 10.10 показано умовне позначення
дешифратора 4х10 (наприклад, мікросхем К555ІД1, К564ІД1). Схема має активні
поодинокі вихідні сигнали.
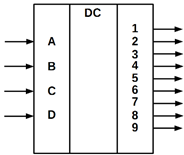
Рисунок 10.10 – Умовне позначення дешифратора 4х10
10.2.1.4. Дешифратор BCD-коду в
семисегментний код
Подібну назву має перетворювач двійково-десяткового (BCD) коду в код
семисегментний індикатора десяткових цифр.
10.2.1.4.1. Семисегментний індикатор на
світлодіодах
Дуже поширеним вихідним пристроєм відображення десяткових чисел є
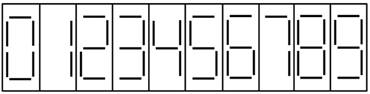
семисегментний індикатор. Сім сегментів індикатора позначені буквами від а до g
(рисунок 10.11, а).
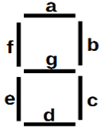
а)
б)
Рисунок 10.11 – Умовне позначення індикатора і його сегментів
Спосіб зображення десяткових цифр від 0 до 9 показаний на рисунку 10.11, б.
Так, якщо світяться сегменти a, b і c, то на індикаторі з'являється десяткова
цифра 7. Якщо світяться всі сегменти від a до g, то з'являється цифра 8. Існує
кілька різновидів індикаторів: на рідких кристалах (РКІ), розжарювальну
(подібний на звичайні лампам розжарювання), світлодіодна і т.д. [3]
Основною частиною світлодіода [18] є діод з площинним pn – переходом. Коли діод включений в прямому напрямку, через pn, то перехдом протікає струм і виникає
випромінювання, яке фокусується в індикаторі спеціальною лінзою, щоб його можна
було спостерігати у вигляді загоряння певного сегмента.
Схема включення одного світлодіода (сегмента) показано на рисунку 10.12,а.
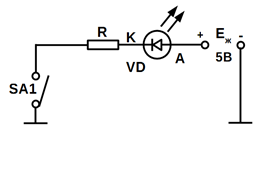
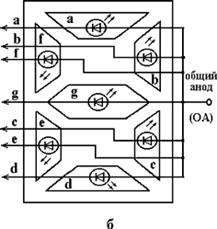
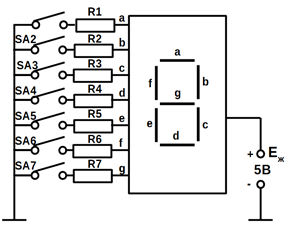
Рисунок 10.12 – Схема включення світлодіода одного сегмента а) і в) і індикатор на рідких
кристалах б)
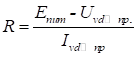 (10.6)
(10.6)
Коли ключ SA1
замкнутий, то струм від джерела ![]() тече через
світлодіод, викликаючи його світіння. Послідовно включений резистор обмежує
струм до рівня приблизно (10...20) мА. Без обмежень резистора світлодіод може
вийти з ладу. Зазвичай, на виходах світлодіодів при випромінюванні допускається
напруга (UVD.пр) не більше
(1,7...2) В. Як і всякий діод, світлодіод чутливий до полярності прикладеної
напруги. Щоб він був включений в прямому напрямку, катод (К) повинен бути
підключений до негативного полюса джерела живлення (землі), а анод (А) – до
його позитивного полюса.
тече через
світлодіод, викликаючи його світіння. Послідовно включений резистор обмежує
струм до рівня приблизно (10...20) мА. Без обмежень резистора світлодіод може
вийти з ладу. Зазвичай, на виходах світлодіодів при випромінюванні допускається
напруга (UVD.пр) не більше
(1,7...2) В. Як і всякий діод, світлодіод чутливий до полярності прикладеної
напруги. Щоб він був включений в прямому напрямку, катод (К) повинен бути
підключений до негативного полюса джерела живлення (землі), а анод (А) – до
його позитивного полюса.
Пристрій семисегментний індикатора на світлодіодах показано на рисунку
10.12, б. У кожному сегменті (від а
до g) міститься світлодіод і
фокусується лінза. Аноди всіх світлодіодів з'єднані разом і підключені з
правого боку індикатора до одного висновку - загальному анода (ОА). Катоди
кожного світлодіода пов'язані із зовнішніми висновками, позначеними a, b, c, ... g. Індикатор (рисунок
10.12, б) в належить до семісегментного світлодіодного індикатора із загальним
анодом. Існують індикатори із загальним катодом [15].
На рисунку 10.13, показано управління сегментами індикатора за допомогою
механічних перемикачів. При замиканні одного з ключів SA1...SA7
струм від ![]() тече: через
вибраний сегмент, обмежувальний резистор і замкнуті контакти перемикача - на
землю (-Ежив). При цьому
обраний сегмент буде світитися (випромінювати). Якщо, наприклад, ми захочемо
висвітити на індикаторі десяткову цифру 7, то необхідно замкнути ключі SA1, SA2 і SA3, щоб вони випромінювали сегменти а, b і
с. Якщо хочемо висвітити цифру 5, то необхідно замкнути ключі SA1, SA3, SA4, SA6 і SA7, які заземлюють катоди сегментів a, c, d, f і g. Слід звернути увагуна
те, що в світлодіодному індикаторі із загальним анодом для активізації
(запалювання) сегментів необхідно подати потенціал землі (логічний нуль) на
висновок, що відповідає обраному сегменту.
тече: через
вибраний сегмент, обмежувальний резистор і замкнуті контакти перемикача - на
землю (-Ежив). При цьому
обраний сегмент буде світитися (випромінювати). Якщо, наприклад, ми захочемо
висвітити на індикаторі десяткову цифру 7, то необхідно замкнути ключі SA1, SA2 і SA3, щоб вони випромінювали сегменти а, b і
с. Якщо хочемо висвітити цифру 5, то необхідно замкнути ключі SA1, SA3, SA4, SA6 і SA7, які заземлюють катоди сегментів a, c, d, f і g. Слід звернути увагуна
те, що в світлодіодному індикаторі із загальним анодом для активізації
(запалювання) сегментів необхідно подати потенціал землі (логічний нуль) на
висновок, що відповідає обраному сегменту.
Для керування роботою індикатора (рисунок 10.12) використовувалися
механічні перемикачі. Зазвичай, керуючі сигнали формуються інтегральними
мікросхемами, наприклад, дешифратором BCD-коду в семисегментний код.
Нижче показані зображення такого дешифратора на електричних схемах (рисунок
10.13, а) і його підключення до семісегментного світлодіодноого індикатора із
загальним анодом (рисунок 10.13, б).
а)
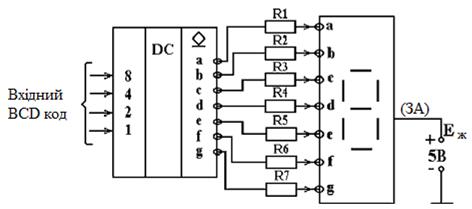
б)
Рисунок 10.13 – Електрична схема управління семисегментним індикатором
В якості дешифраторів BCD-коду в семисегментний можуть використовуватися
різні мікросхеми, наведені в [4, 15].
Наприклад, ІМС К514ІД2, позначення якої дано на рисунку 10.13, а, має
відкриті колекторні виходи і використовується спільно з індикаторами, що мають
загальний анод. При цьому потрібно застосувувати зовнішні резистори, що
включаються між виходами дешифратора і входами індикатора (рисунок 10.13, б).
Допустимий струм мікросхеми дешифратора по кожному виходу становить 22 мА.
Окрім інформаційних входів, на які надходить двійково-десятковий код,
індикатори можуть містити ряд керуючих входів [4, 15, 18], наприклад, для
придушення нулів, гасіння, контролю свічення, синхронізації і т.д.
10.2.2. Мультиплексори і
демультиплексори
У сучасних мікропроцесорних пристроях управління і однокристальних мікроЕОМ
широко застосовуються КЦП, що здійснюють підключення (коммутировання) виходу
одного з паралельно включених цифрових пристроїв на загальну шину або, навпаки,
з'єднання загальної шини з входом одного з декількох паралельно включених
пристроїв. Ці функції виконують пристрої, названі мультиплексорами і
демультиплексорами.
10.2.2.1. Мультиплексори
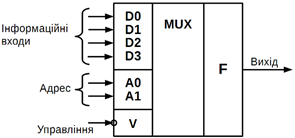
Мультиплексор – це комбінаційний цифровий пристрій, який сполучає (комутує)
один з декількох інформаційних вхідних сигналів з одним загальним виходом.
Приклад позначення мультиплексора на електричних схемах показаний на рисунку 10.14.
Пристрій містить вісім інформаційних входів: D0, D1,...,D7; трьи адресних
входи: А0, А1, А2 і один синхронізуючий вхід V.
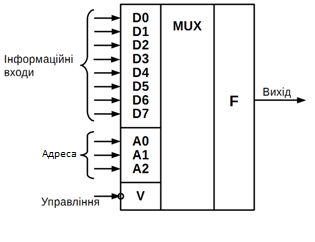
Рисунок 10.14 – Умовне позначення мультиплексора
Залежно від комбінації адресних сигналів А0, А1, А2 він забезпечує комутацію одного з восьми інформаційних вхідних
сигналів Di на загальний
вихід F. Нульовий синхросигнал на вході V дозволяє передати
інформацію з вибраного входу на вихід. Булевий вираз, що описує функціонування
розглянутого мультиплексора має вигляд:
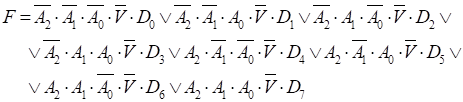 (10.7)
(10.7)
Приклад реалізації мультиплексора 4х1.
Мультиплексор можна реалізувати за допомогою логічних елементів заданого
базису. У його структуру можна ввести і більш складні цифрові пристрої,
наприклад, перетворювач двійкового коду у десятковий (дешифратор).
На рисунку 10.15, а наведено приклад реалізації мультиплексора з чотирма
інформаційними входами на ЛЕ базису І, АБО, НЕ і дешифраторі, а на рисунку
10.15, б показано його функціональне позначення. Якщо V = 0, то F = 0 незалежно
від інформаційних сигналів.
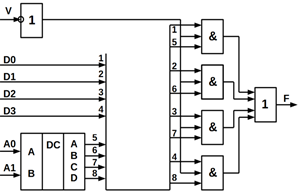
а) б)
Рисунок 10.15 – Функціональна схема мультиплексора: а) умовне позначення; б) з 4-ма керуючими
входами
Схема реалізує булевий вираз:
![]() (10.8)
(10.8)
Існують мультиплексори в інтегральному виконанні, наприклад, ІМС К555КП2
(рисунок 10.16).
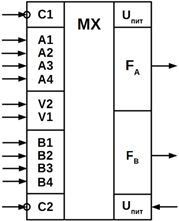
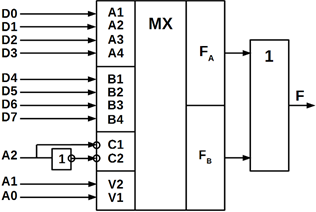
а)
б)
Рисунок 10.16 – Умовне позначення мультиплексора в інтегральному виконанні
виконаного на мікросхемі К555КП2
Мультиплексор КП2 (рисунок 10.16, а) містить два мультиплексори 4x1 із
загальними адресними входами. Він складається з двох частин, кожна з яких
містить чотири інформаційних канали А1 ... А4 (В1 ... В4); і один вихід FА
(FВ). Керуючі (адресні) входи V2, V1 є загальними, тобто сигнали на них чинять
одночасний вплив на обидві частини ІМС. Правила роботи схеми відображає таблиця
10.5.
Для
збільшення числа каналів об'єднують кілька мультиплексорів, використовуючи для
цієї мети стробування входів, як це показано на рисунку 10.16, б. Ця схема
реалізує мультиплексор 8х1 (таблиця 10.6).
Таблиця 10.5 – Правила роботи схеми
|
Стробування входи С1, С2 |
Управляючі входи |
Вихід FA |
Вихід FB |
|
|
V2 |
V1 |
|||
|
0 |
0 |
0 |
A1 |
B1 |
|
0 |
0 |
1 |
A2 |
B2 |
|
0 |
1 |
0 |
A3 |
B3 |
|
0 |
1 |
1 |
A4 |
B4 |
|
1 |
X |
X |
0 |
0 |
|
Примітка: X – будь-яке значениям: 0 або 1 |
||||
Таблиця
10.6 – Реалізація мультиплексора 8х1
|
№ |
А2 |
А1 (V2) |
А0 (V1) |
F |
|
0 |
0 |
0 |
0 |
D0 |
|
1 |
0 |
0 |
1 |
D1 |
|
2 |
0 |
1 |
0 |
D2 |
|
3 |
0 |
1 |
1 |
D3 |
|
4 |
1 |
0 |
0 |
D4 |
|
5 |
1 |
0 |
1 |
D5 |
|
6 |
1 |
1 |
0 |
D6 |
|
7 |
1 |
1 |
1 |
D7 |
10.2.2.2. Демультиплексори
Демультиплексор
– це КЦУ, яке з'єднує (комутує) загальний інформаційний вхід з одним з
декількох виходів відповідно до заданого кодом на керуючих (адресних) входах.
Іншими словами, демультиплексори вирішують завдання, зворотні
мультиплексуванню. Приклад позначення демультиплексора на електричних схемах
показаний на рисунку 10.17, a.
Схема має
чотири інформаційних виходи і два адресних входи А0 і А1.
Булеві вирази, що описують роботу даного демультиплексора, мають вигляд:
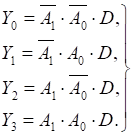 (10.9)
(10.9)
Такими ж виразами визначається робота дешифратора з синхровходу V (рисунок 10.17, б). Тому його можна
використовувати в якості демультиплексора, якщо інформаційний вхідний сигнал
подавати на вхід V.
а)
б)
Рисунок 10.17 – Умовне зображення мультиплексорів
10.2.2.3. Мультиплексори-селектори
(мультиплексори-демультиплексори)
Мультиплексори-селектори є двонаправленими, оскільки дозволяють комутувати
цифрові й аналогові сигнали в обох напрямках, і тому можуть бути використані не
тільки в якості мультиплексора для комутації одного з входів на вихід, але і в
якості селектора (демультиплексора) для комутації входу на один з виходів .
Нижче показані: позначення мультиплексора-селектора (демультиплексора) на
електричних схемах (рисунок 10.18, а) і його спрощена внутрішня структура
(рисунок 10.18, б).
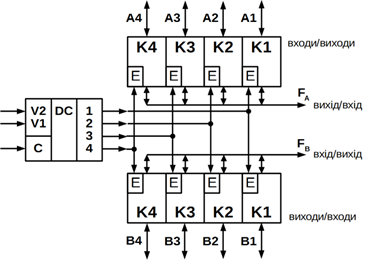
Пристрій містить дві групи двонаправлених ключів (К1...К4) і дешифратор. Вихідні сигнали
дешифратора впливають на керуючі входи ключів (Е) і визначають їх стан. При Е = 0 ключ закритий, а при Е=1 – відкритий і утворює низькоомний ланцюг
розповсюдження сигналу через нього. Такий ключ називають аналоговим, оскільки
він забезпечує неспотворену двосторонню передачу сигналів. Кожен ключ має два рівнозначних виведення, кожний з яких
може бути входом або виходом. За одним з висновків ключі об'єднані у дві групи FА і FВ,
які утворюють виходи мультиплексорів і входи демультиплексорів.
а)
б)
Рисунок 10.18 – Мультиплексор-селектор: а) умовне зображення;
б) електрична схема з'єднань
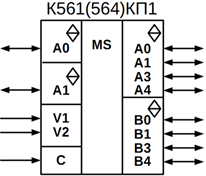
Структуру, представлено на рисунку 10.18, б, має мікросхема К561 (564) КП1,
виконана за КМОН-технологією та містить два мультиплексора-селектора, керовані
від загальних входів V1, V2
і С (рисунок 10.18, а). При
одиничному керуючому сигналі на вході З
ключі розімкнуті і виходи знаходяться у 3-му стані.
Суматор призначений для складання двох чисел, заданих у двійковому коді. З
прикладу, наведеного на рисунку 10.20, видно, що правила складання десяткових і
двійкових чисел однакові:
1) складання виробляється по-розрядно від молодшого розряду до старшого;
2) сума молодших розрядів доданків А0
і В0 записується у
відповідній системі числення однозначним числом S0 або двозначним числом P0S0, де Р0
називається перенесенням з нульового розряду у сусідній розряд;
3) у всіх наступних розрядах знаходиться сума даних розрядів доданків Ai, Bi і перенесення Pi-1
від складання попередніх розрядів (у прикладах на рисунку 10.19 цей випадок
позначений зірочкою).
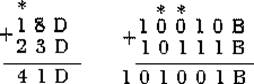
Рисунок
10.19 – Правила складання десяткових і двійкових
чисел
Сказане
відображає таблиця істинності однорозрядного двійкового повного суматора
(таблиця 10.6).
Таблиця
10.6 – Таблиця істинності
|
N набору |
Аi |
Bi |
Pi-1 |
Si |
Pi |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
0 |
|
2 |
0 |
1 |
0 |
1 |
0 |
|
3 |
0 |
1 |
1 |
0 |
1 |
|
4 |
1 |
0 |
0 |
1 |
0 |
|
5 |
1 |
0 |
1 |
0 |
1 |
|
6 |
1 |
1 |
0 |
0 |
1 |
|
7 |
1 |
1 |
1 |
1 |
1 |
Булеві
вирази логічних функцій Si
і P в СДНФ мають вигляд:
![]() , (10.10)
, (10.10)
![]() . (10.11)
. (10.11)
Вираз (10.11)
можна мінімізувати. У результаті отримаємо:
![]() . (10.12)
. (10.12)
На
підставі виразів (10.10) і (10.12) однорозрядний двійковий повний суматор може
бути реалізований в базисі І, АБО, НІ (рисунок 10.20).
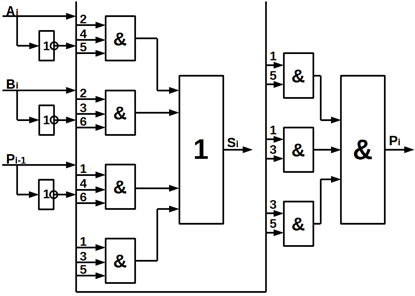
Рисунок
10.20 – Схема реалізації однорозрядного двійкового суматора
Використовуючи
правила переходу з базису І, АБО, НЕ у базис І-НЕ і АБО-НЕ, можна побудувати
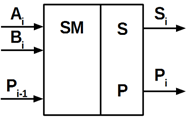
однорозрядних повний суматор в двох інших базисах.
Позначення
однорозрядного суматора на електричних схемах наведено на рисунку 10.21.
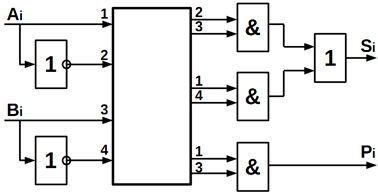
Півсуматор,
на відміну від повного суматора, забезпечує виконання операції підсумовування
двох однорозрядних двійкових чисел Ai
і Bi без урахування
сигналу переносу. У результаті складання поряд з сумою може вийти перенос.
Функціонування півсуматора описується в таблиці 10.7.
Як видно
з таблиці 10.7, для реалізації функції Si
необхідний елемент "нерівнозначність" (суматор за модулем два), а для
реалізації функції Pi –
логічне І. Булеві вирази для Si і
Pi в СДНФ мають вигляд:
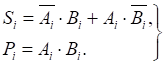 (10.13)
(10.13)
Таблиця
10.7 – Функціонування півсуматора
|
N набору |
Аi |
Bi |
Si |
Pi |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
0 |
|
2 |
1 |
0 |
1 |
0 |
|
3 |
1 |
1 |
0 |
1 |
Приклад
проектування півсуматора на логічних елементах.
На
рисунку 10.21. наведена схема, реалізує вираз (10.11) на елементах І, АБО, НІ.
Рисунок
10.21 – Схема реалізації суматора по функцією (10.13)
Для
отримання більш простої схеми одноразрядного півсуматора на логічних елементах
функцію Si краще уявити у
СКНФ (таблиця 10.7)
![]() (10.14)
(10.14)
Виконавши
перетворення за теореміою де Моргана, отримаємо:
![]() (10.15)
(10.15)
де, ![]() (10.13).
(10.13).
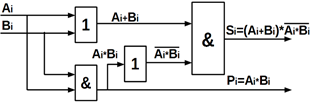
Вираз (10.15) реалізується схемою (рисунок 10.22).
а)
б)
в)
г)
Рисунок
10.22 – Схеми суматорів реалізують логічні вирази
Якщо
порівняти цю схему зі схемою, що реалізує вираз (10.13), то схема на рисунку
10.21, а виглядає простіше.
Умовні
графічні позначення півсуматора і повного одноразрядного суматора на
електричних схемах показані на рисунку 10.22 б, в, а схема повного
одно-разрядного суматора, виконаного на двох півсуматорах, показана на рисунку
10.22.
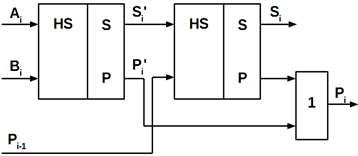
Для
складання n-розрядних чисел необхідно (n-1)
однорозрядних повних суматорів і один півсуматор у нульовому розряді (рисунок
10.23).
У цьому
суматорі реалізована послідовна передача перенесення з одного розряду в інший.
При великій кількості розрядів сумуючих чисел тривалість підсумовування в
суматорах з послідовним перенесенням може виявитися неприпустимо великим.
Великою швидкодією володіють суматори з паралельним переносом, містять схему
прискореного перенесення.
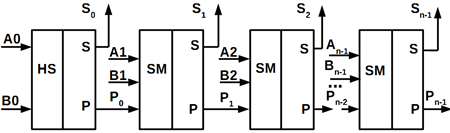
Рисунок
10.23 – Функціональна схема суматора, де реалізована послідовна передача
перенесення з одного розряду в інший
10.2.4. Пристрої контролю парності
(ПКП)
Призначені
для перевірки довічних кодових комбінацій, що надходять на їх входи, на
наявність в них парного (непарного) числа одиниць. Таке КЦУ має n входів, рівне кількості розрядів
вхідного ДК, і один вихід. На виході формується напруга високого рівня тільки в
тому випадку, якщо число одиниць у вхідному коді непарне. Основу схеми контролю
парності становить суматор за модулем два, який реалізує логічну операцію.
![]() .
(10.16)
.
(10.16)
Для двох змінних ця операція може бути виконана логічним елементом
"ВИКЛЮЧАЄ АБО", який реалізує логічну функцію.
![]() . (10.17)
. (10.17)
Функція F має значення одиниці
тільки в тому випадку, якщо в наборі з двох змінних є одна одиниця, в інших
випадках значення функції дорівнює нулю.
Нижче показані: склад мікросхеми К555ЛП5, що включає 4 двохвходових
суматора за модулем два (рисунок 10.24, а), приклад побудови на основі ІМС
К555ЛП5 пристрої контролю парності 8-розрядного ДК (рисунок 10.24, б) і
позначення мікросхеми К561СА1, що є пристроєм контролю парності 12 -розрядних
двійкових кодів (рисунок 10.24, в).
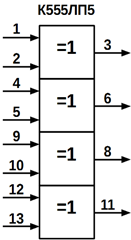
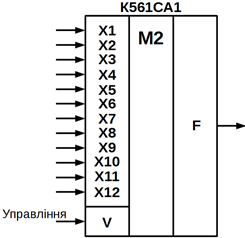
а)
б)
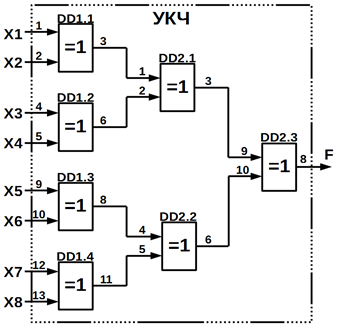
в)
Рисунок 10.24 – Мікросхеми двохвходових суматорів за модулем 2;
в) приклад побудови суматора на інтегральних мікросхемах
Якщо V = 0, то:
парне à F = 0; ü
ý F доповнює до парності.
непарне à F = 1;þ
Якщо V = 1, то:
парне à F = 1; ü
ý F доповняє до непарності.
непарне à F = 0;þ
Порівнюють два числа, представлених у двійковому коді, ![]() і
і ![]() і формують ознаки
результату порівняння у вигляді напруги високого рівня на одному з виходів: FA = B, FA <B, FA> B.
і формують ознаки
результату порівняння у вигляді напруги високого рівня на одному з виходів: FA = B, FA <B, FA> B.
Найбільш простою є схема формування ознаки рівності двох чисел
(рисунок 10.23).
Такий компаратор включає логічний елемент АБО-НЕ, на входи якого подаються
результати порозрядного додавання за модулем два.
Схема реалізує логічну функцію.
![]() (10.18)
(10.18)
Після перетворення (10.18) за теоремою де Моргана отримаємо:
![]() . (10.19)
. (10.19)
Враховуючи, що ![]() =
=![]() – нееквівалентність (і
сума за модулем два для двох змінних), вираз (10.19) прийме вигляд:
– нееквівалентність (і
сума за модулем два для двох змінних), вираз (10.19) прийме вигляд:
![]() , (10.20)
, (10.20)
що відповідає рисунок 10.25.
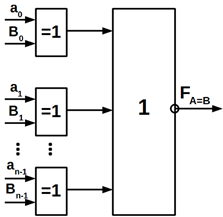
Рисунок 10.25 – Схема формування ознаки рівності
Якщо А = В, то F = 1, якщо А¹В, то F = 0.
Нижче показані: позначення 4-вхідного компаратора на електричних схемах
(рисунок 10.26, а) і приклад його реалізації на суматорі і логічних елементах
І, АБО-НЕ, НЕ (рисунок 10.26, б).
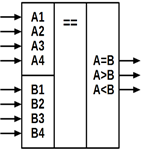
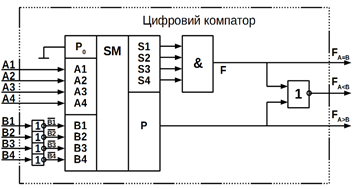
а) б)
Рисунок 10.26 – 4-вхідний компаратор: а) умовне зображення;
б) функціональна схема.
10.3. Використання для проектування КЦП
мультиплексорів, дешифраторів і постійних запам'ятовуючих пристроїв
У зв'язку з тим, що багато серії ІМС містять у своєму складі
мультиплексори, дешифратори і постійні запам'ятовуючі пристрої (ПЗУ), то
розглянемо можливість реалізації на їх основі різних КЦУ. У ряді випадків,
особливо при великому числі вхідних змінних і значній кількості виходів це
дозволяє зменшити загальне число необхідних корпусів мікросхем.
10.3.1. Побудова КЦП на
мультиплексорах
В якості прикладу розглянемо реалізацію за допомогою восьмивходового
мультиплексора (рисунок 10.27) мажоритарного елементу, функціонування якого
описано таблицею істинності (таблиця 10.8).
На адресні входи мультиплексора подаються вхідні логічні змінні Х1, Х2, Х3,
а на інформаційних входах D0 ...D7 зафіксовані значення
реалізованої логічної функції на наборах логічних змінних, номери яких
співпадають з номерами інформаційних входів мультиплексора.
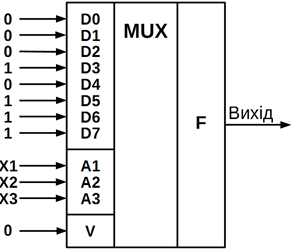
Рисунок 10.27 – Схема мультиплексора
Є можливість вдвічі скоротити необхідне число інформаційних входів
мультиплексора (а, отже, використовувати більш просту його структуру), якщо на
ці входи подати не тільки фіксовані рівні логічних одиниць і нулів, а й
значення окремих вхідних змінних Х.
Для цього ще раз зобразимо таблицю істинності проектованого мажоритарного
елементу, розділивши її на чотири групи по два рядки в кожній (таблиця 10.9).
У межах кожної групи можливі тільки чотири значення вихідної булевої
функції F: нульове значення на обох
наборах – гр.1; одиничне значення на обох наборах – гр.4: збіг функції F зі змінною Х1 (набори 2, 3, 4, 5): протилежні значення функції F і змінної Х1 (у даному прикладі відсутні).
Таблиця 10.8 –Функціонування восьмивходового мультиплексора
|
№ набору |
X3 |
X2 |
X1 |
F |
|
|
0 |
0 |
0 |
0 |
0 |
Y0 |
|
1 |
0 |
0 |
1 |
0 |
Y1 |
|
2 |
0 |
1 |
0 |
0 |
Y2 |
|
3 |
0 |
1 |
1 |
1 |
Y3 |
|
4 |
1 |
0 |
0 |
0 |
Y4 |
|
5 |
1 |
0 |
1 |
1 |
Y5 |
|
6 |
1 |
1 |
0 |
1 |
Y6 |
|
7 |
1 |
1 |
1 |
1 |
Y7 |
Таблиця 10.9 –
Таблиця істинності проектованого мажоритарного елементу
|
|
|
(A2) |
(A1) |
|
|
Інформаційні входи мультиплексора 4x1 (Рисунок 10.28) |
|
|
№ набору |
X3 |
X2 |
X1 |
F |
D |
|
Гр.1 |
0 |
0 |
0 |
0 |
0 |
D0=0 |
|
1 |
0 |
0 |
1 |
0 |
||
|
Гр.2 |
2 |
0 |
1 |
0 |
0 |
D1=X1 |
|
3 |
0 |
1 |
1 |
1 |
||
|
Гр.3 |
4 |
1 |
0 |
0 |
0 |
D2=X1 |
|
5 |
1 |
0 |
1 |
1 |
||
|
Гр.4 |
6 |
1 |
1 |
0 |
1 |
D3=1 |
|
7 |
1 |
1 |
1 |
1 |
Отже, для реалізації відповідного КЦУ можна використовувати
чотирьохвходовий мультиплексор, на адресні входи якого подаються змінні Х3 і Х2, а на інформаційні входи D – значення відповідно до останнього стовпця таблиці 10.9 (рисунок
10.28).
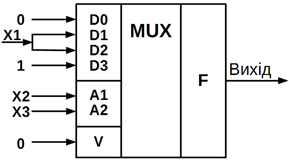
Рисунок 10.28 – Чотиривходовий мультиплексор
У результаті є можливість зменшити апаратні витрати, використовуючи для
реалізації трьох входового мажоритарного елементу лише половину мікросхеми
К555КП2.
10.3.2. Побудова КЦП на
дешифратор
Для побудови КЦУ можна використовувати дешифратори. Так як активне значення
сигналу на кожному виході дешифратора визначає одну з комбінацій вхідних
сигналів, то, об'єднуючи за допомогою відповідних логічних елементів деякі
вихідні сигнали дешифратора, можна реалізувати КЦП, задане таблицею істинності,
з числом наборів, що не перевищує число виходів використовуваного дешифратора.
Розглянемо приклад реалізації трьохвходового мажоритарного елементу
(таблиця 10.8) на трьохвходовому дешифраторі.
Для виходів дешифратора Yi з активними одиничними значеннями вихідних сигналів (рисунок
10.29, а) можна записати:
![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;![]() .
.
У такому випадку в СДНФ функція мажоритарна відповідно до таблиці 10.8 може
бути представлена у вигляді:
![]() (10.21)
(10.21)
Цей вираз і реалізує схема на рисунку 10.29, а.
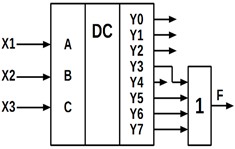
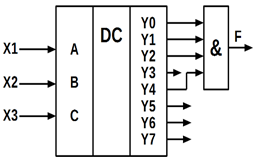
а)
б)
Рисунок 10.29 – Трьохвходовий дешифратор з активними нульовими значеннями
Уявімо ту ж функцію в СКНФ і зробимо деякі перетворення за теоремою де
Моргана:
![]()
![]() . (10.22)
. (10.22)
Проаналізувавши отриманий вираз, а також вирази для Yi, наведені вище, можна остаточно записати:
![]() .
(10.23)
.
(10.23)
У цьому випадку трьохвходовий мажоритарний елемент може бути реалізований
на трьохвходовому дешифраторі з активними нульовими значеннями вихідних
сигналів (рисунок 10.29, б).
Якщо порівняти між собою реалізації КЦУ на основі мультиплексорів і
дешифраторів, то можна відзначити менші апаратні витрати при використанні
мультиплексорів. Однак у конкретних умовах проектування КЦУ може виявитися
доцільним застосування для цих цілей і дешифраторів, наприклад, коли половина
мікросхеми здвоєного дешифратора вже використана у складі проектованого
пристрою, а інша половина залишилася вільною і може бути застосована для
побудови якогось КЦП.
10.3.3. Побудова КЦП на
постійному запам'ятовуючому пристрої (ПЗП)
ПЗУ предсавляє собою велику інтегральну схему (ВІС), що має N
входів і М виходів. Спрощена
структура ПЗУ при ![]() і
і ![]() наведена на рисунку
10.30, а. На вході схеми встановлений дешифратор, перетворюючий комбінації
двохрозрядного двійкового коду в чотирьохпозиційний унітарний (десятковий) код.
При кожній комбінації вхідного ДК на одному з виходів дешифратора з'являється
логічна 1, а на інших – нулі.
наведена на рисунку
10.30, а. На вході схеми встановлений дешифратор, перетворюючий комбінації
двохрозрядного двійкового коду в чотирьохпозиційний унітарний (десятковий) код.
При кожній комбінації вхідного ДК на одному з виходів дешифратора з'являється
логічна 1, а на інших – нулі.
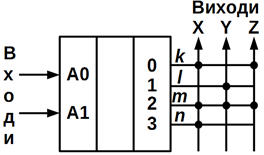
a)
б)
Рисунок
10.30 – Умовна схема взаємозв'язків між дешифратором і ПЗП
Між виходами дешифратора k, l, m, n
і вихідними шинами ПЗУ X, Y, Z
включені ланцюжки з двох послідовно включених діодів VD1 і VD2.
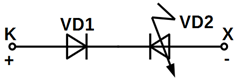
На рисунку 10.30, б, як приклад показано зв'язок між вихідною шиною до
дешифратора і виходом Х ПЗУ. У вихідному стані ланцюжки,
що зв'язують виходи дешифратора і виходи ПЗУ, струм не проводять і зв'язки між
шинами k, l, m, n і Х, Y, Z відсутні. При цьому з усіх
виходів X, Y, Z знімаються логічні
нулі.
Користувач на спеціальному пристрої – програма торі – створює потрібні
зв'язки між шинами, подаючи пробивні напруги між певними точками. При цьому
відповідні діоди пробиваються, наприклад VD2
(рисунок 10.30, б), і надалі можуть розглядатися як короткозамкнені.
На рисунку 10.30 а, кружечками показані створені постійні зв'язки, за
допомогою яких реалізується таблиця істинності комбінаційного пристрою з трьома
виходами (таблиця 10.10).
Таблиця 10.10
– Таблиця істинності комбінаційного пристрою
|
N |
B |
A |
X |
Y |
Z |
|
|
0 |
0 |
0 |
1 |
0 |
1 |
k |
|
1 |
0 |
1 |
0 |
1 |
0 |
l |
|
2 |
1 |
0 |
1 |
1 |
1 |
m |
|
3 |
1 |
1 |
1 |
0 |
0 |
n |
Наприклад,
при комбінації вхідних логічних змінних А
= 1, В = 0 з виходів знімаються
сигнали Х = 0; Y = 1; Z = 0. Таким чином
на ПЗУ можна реалізувати потрібну таблицю істинності комбінаційного пристрою,
що має кілька виходів. Одна схема ПЗУ може замінити велике число логічних
мікросхем малого і середнього рівня інтеграції, тому ПЗУ можуть ефективно
використовуватися для створення складних комбінаційних пристроїв. Крім того,
ПЗУ знаходять широке застосування як елементи постійної пам'яті, в які
заносяться програми, що керують роботою мікропроцесорів і однокристальних мікроЕОМ.

