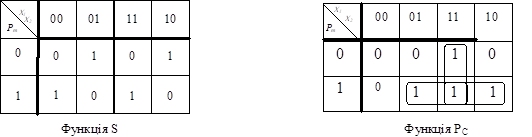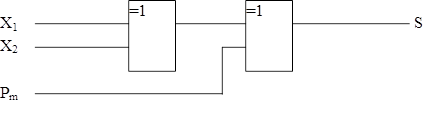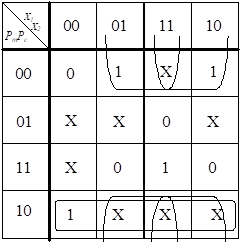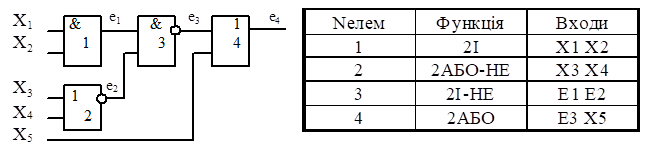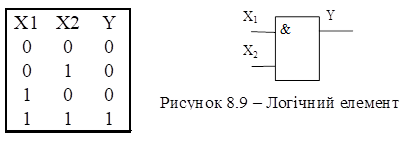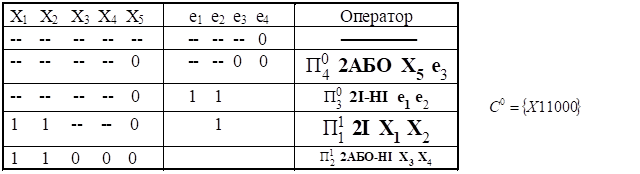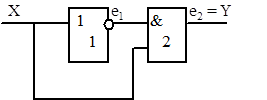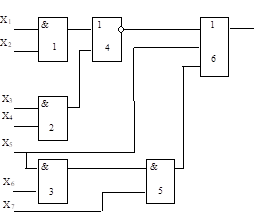Тема 11. Методи аналізу і синтезу комбінаційних схем

Технічним аналогом булевої функції в обчислювальній техніці є, так звана, комбінаційна схема, на вхід якої надходять і з виходу знімаються електричні сигнали у вигляді одного з рівнів напруги, що відповідають значенням логічного 0 і логічної 1-ці.

Для з'ясування поняття комбінаційної схеми, розглянемо схему S, що має m входів і n виходів (рисунок 8.1). На її входи можуть бути подані набори значень вхідних змінних X_i {0,1}, а на виходах формуються вихідні змінні Y_jÎ{0,1},.

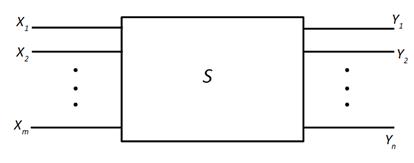
Рисунок 8.1 – Загальне позначення комбінаційних схем

Схема S називається комбінаційною, якщо кожну з n функцій її виходів Y1, Y2, ..., Yn можна представити як булеву функцію вхідних змінних X1, X2, ..., Xm.

Комбінаційна схема описується за допомогою системи рівнянь (8.1), де F_i – булева функція.

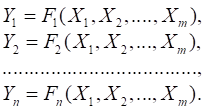(8.1)

Як випливає з визначення комбінаційної схеми, значення вихідних змінних Y_j у довільний момент часу однозначно визначаються значеннями вхідних змінних X_i.

Структурно комбінаційна схема може бути представлена, як сукупність елементарних логічних схем – логічних елементів (ЛЕ). ЛЕ виконують над вхідними змінними елементарні логічні операції типу І – НІ, І, АБО, АБО – НІ
і т.д. Число входів логічного елемента відповідає числу аргументів відтворюваної ним булевої функції. Графічне зображення комбінаційної схеми, за якого показано зв'язки між різними елементами, а самі елементи представлені умовними позначеннями, називаються функціональною схемою.

У ході розробки комбінаційних схем доводиться вирішувати завдання аналізу та синтезу.

Завдання аналізу полягає у визначенні статичних та динамічних властивостей комбінаційної схеми. У статиці визначаються булеві функції, реалізовані комбінаційної схемою за відомою їй структурою. У динаміці розглядається здатність надійного функціонування схеми в перехідних процесах за зміни значень змінних на входах схеми, тобто, визначається наявність на виходах схеми можливих небажаних імпульсних сигналів, що не йдуть безпосередньо з виразів для булевих функцій, реалізованих схемою.

Завдання синтезу полягає в побудові із заданого набору логічних елементів комбінаційної схеми, реалізує задану систему булевих функцій.

Рішення завдання синтезу не є однозначним, можна запропонувати різні варіанти комбінаційних схем, що реалізують одну й ту ж систему булевих функцій, але відрізняються за тими чи іншими параметрами. Розробник комбінаційних схем з цієї безлічі варіантів вибирає один, виходячи з додаткових критеріїв: мінімальної кількості логічних елементів, необхідних для реалізації схеми, максимальної швидкодії і т.д. Існують різні методи синтезу комбінаційних схем, серед яких найбільш розроблений канонічний метод.

8.1 Канонічний метод синтезу комбінаційних схем

Як зазначалося вище, комбінаційна схема (КС) може мати кілька виходів. За канонічного методу передбачається, що кожна вихідна функція реалізується своєю схемою, сукупність яких і дає необхідну КС. Тому синтез складної КС з
n-виходами замінюється синтезом n-схем з одним виходом.

Згідно з канонічним методом синтез КС включає в себе ряд етапів.

1. Підлягаюча реалізації булева функція (або її заперечення) представляється у вигляді СДНФ.

2. З використанням методів мінімізації визначається мінімальна ДНФ (МДНФ) або мінімальна КНФ (МКНФ). З отриманих двох мінімальних форм вибирається більш проста.

3. Булеву функцію в мінімальній формі згідно з п. 2 представляють у заданому (або обраному розробником) базисі.

4. За поданням функції в заданому базисі будують комбінаційну схему.

Необхідно відзначити, що підлягаюча реалізації булева функція F (X₁, X₂, ..., X_m) може бути задана не на всіх можливих наборах аргументів X₁, X₂, ..., X_m. На тих наборах, де функція невизначена, її довизначають так, щоб у результаті мінімізації отримати більш просту МДНФ або МКНФ. При цьому спроститься і сама КС. Крім того, досить часто з метою отримання ще більш простого представлення функції МДНФ, отримана в п. 2, представляється в так званій формі, тобто, виносяться за дужки загальні частини імплікант МДНФ.

Розглянемо канонічний метод синтезу на прикладі побудови схеми повного однорозрядного двійкового суматора.

Як відомо з курсу машинної арифметики, повний однорозрядний суматор – це пристрій, який здійснює складання за mod 2 відповідних розрядів (X1, X2) двійкових чисел з урахуванням переносу (Р_m) у даний розряд із сусіднього молодшого розряду суми. Суматор виробляє цифру результату (S) в даному розряді і перенесення (Рс) в сусідній старший розряд суми. Таблиця істинності такого суматора (тобто, подання булевої функції, яку він реалізує, у вигляді СДНФ), представлена у таблиці 8.1.

Необхідно отримати булеві функції Карти Карно для цих функцій наведені нижче (рисунок 8.2).

Таблиця 8.1 – Таблиця істинності повного одноразрядного двійкового суматора

X₁	0	0	0	1	1	1	1
X₂	0	1	1	0	0	1	1
P_m	1	0	1	0	1	0	1
S	1	1	0	1	0	0	1
P_c	0	0	1	0	1	1	1

Рисунок 8.2 – Карти Карно для функцій S- і P_c-суматора

Як випливає з наведених карт, ДНФ відповідних функцій має вигляд:

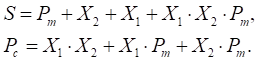(8.2)

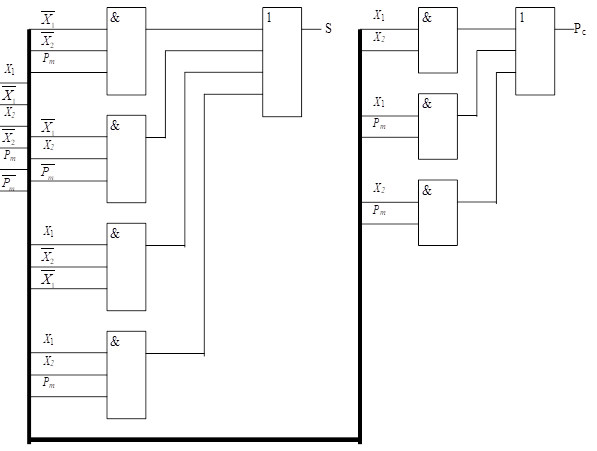
Отримана система булевих функцій представлена в базисі І, АБО, НЕ. Відповідна їй КС наведена на рисунку 8.3.

Отриману комбінаційну схему можна спростити, винести за дужки загальні частини у виразах для S і Р_c, однак істотного результату це не дасть (бажано самостійно в цьому переконатися).

Значно спростити схему можна, якщо скористатися іншим базисом, наприклад, логічним елементом "ВИКЛЮЧАЮЧЕ АБО". У цьому випадку вираз для S можна записати S = (X₁ + X₂ + Р_m) mod2 = X₁Å X₂Å Р_m. Тоді схема для S буде мати вигляд (рисунок 8.3).

Рисунок 8.3 – Комбінаційна схема

Іноді для синтезу КС з декількома виходами може використовуватися наступний прийом. Будемо вважати, що під час синтезу схеми суматора функція S є функцією чотирьох змінних: S = f (X₁, X₂, Р_m, Р_с) (рисунок 8.4). Таблиця істинності для цього випадку набуде вигляду, який зображено у таблиці 8.2.

Рисунок 8.4 – Функціональна схема комбінаційного суматора

Таблиця 8.2 – Таблиця істинності суматора

X₁	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
X₂	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
P_m	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
P_c	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
S	X	1	X	1	X	X	0	1	X	X	0	X	0	X	1

Невизначені значення для S відповідають наборам, які ніколи не можуть бути в реальній схемі. Карта Карно для функції S = f (X₁, X₂, P_m, P_c) (рисунок 8.5).

Рисунок 8.5 – Карта Карно для функції S S = f (X₁, X₂, P_m, P_c

У результаті мінімізації:

(8.3)

Порівнюючи вирази (8.2) і (8.3), відзначаємо, що функція S=f(X₁,X₂,P_m,P_c) простіше, ніж функція S=f₁(X₁, X₂, P_m). Схему, відповідну (8.3), пропонується побудувати самостійно.

Задача синтезу має звичайно кілька рішень. Для порівняння різних варіантів комбінаційних схем використовують їх основні характеристики: складність і швидкодію.

8.2 Характеристики комбінаційних схем

Складність схеми оцінюється кількістю устаткування, що становить схему. Під час розробки схем на основі конкретної елементної бази кількість обладнання, зазвичай, вимірюється числом корпусів (модулів) інтегральних мікросхем, що використовуються у схемі. У теоретичних розробках орієнтуються на довільну елементну базу і тому для оцінки витрат обладнання використовується оцінка складності схем за Квайном.

Складність (ціна) за Квайном визначається сумарним числом входів логічних елементів у складі схеми.

За такої оцінки одиниця складності – один вхід логічного елемента. Ціна інверсного входу звичайно приймається рівною двом. Такий підхід до оцінки складності виправданий з наступних причин:

- складність схеми легко обчислюється за булевими функціями, на основі яких будується схема: для ДНФ складність схеми дорівнює сумі кількості букв (букві зі знаком заперечення відповідає ціна 2) та кількості знаків диз'юнкції, збільшеній на 1-цю для кожного диз'юнктивного вираження;

- усі класичні методи мінімізації булевих функцій забезпечують мінімальність схеми саме в сенсі ціни за Квайном.

Практика показує, що схема з мінімальною ціною за Квайном, зазвичай, реалізується найменшим числом конструктивних елементів – корпусів інтегральних мікросхем.

Швидкодія комбінаційної схеми оцінюється максимальною затримкою сигналу під час проходження його від входу схеми до виходу, тобто, визначається проміжком часу від моменту надходження вхідних сигналів до моменту встановлення відповідних значень вихідних. Затримка сигналу кратна числу елементів, через які проходить сигнал від входу до виходу схеми. Тому швидкодія схеми характеризується значенням rt, де t – затримка сигналу на одному елементі. Значення r визначається кількістю рівнів комбінаційної схеми, яке розраховується наступним чином. Входу КС приписується рівень нульової. Логічні елементи, пов'язані тільки з входами схеми, ставляться до рівня ПЕРШОГО. Елемент відноситься до рівня k, якщо він пов'язаний по входах з елементами рівнів k-1, k-2, і т.д. Максимальний рівень елементів r визначає кількість рівнів КС, що називають рангом схеми. Приклад визначення рангу r схеми (рисунок 8.6).

Рисунок 8.6 – Визначення рангу схеми

Як відомо, будь-яка булева функція може бути представлена в ДНФ, якій відповідає дворівнева комбінаційна схема. Отже, швидкодію будь-якої КС в принципі можна звести до 2t.

Мінімізація булевої функції з метою зменшення складності схем, зазвичай, призводить до необхідності подання функцій у дужковій формі, якій відповідають схеми з r>2. Тобто, зменшення витрат обладнання в загальному випадку призводить до зниження швидкодії схем.

8.3 Системи (серії) логічних елементів та їх основні характеристики

Під час побудови КС пристроїв обчислювальної техніки використовуються різні логічні елементи, які повинні узгоджуватися за вхідними і вихідними сигналами, напругою харчування і т.д. Для цієї мети логічні елементи об'єднують у серії.

Серією (системою, комплексом) логічних елементів ЕОМ називається призначений для побудови цифрових пристроїв функціонально повний набір логічних елементів, який поєднується спільними електричними, конструктивними і технологічними параметрами, що використовують однаковий спосіб подання інформації, та тип міжелементних зв'язків. Система елементів найчастіше надлишкова за своїм функціональним складом, що дозволяє будувати схеми більш економічні за кількістю використаних елементів.

До складу серії входять елементи для виконання логічних операцій, що запам'ятовують елементи, що реалізують функції вузлів ЕОМ, а також спеціальні елементи для посилення, відновлення і формування сигналів стандартної форми.

Конструктивно логічні елементи являють собою мікро-мініатюризовані інтегральні електронні схеми (мікросхеми), сформовані в кристалі кремнію за допомогою спеціальних технологічних процесів.

У більшості сучасних серій елементів є мікросхеми малого ступеня інтеграції (ІС до 100 елементів на кристал), середнього ступеня (СІС – до 1000 елементів на кристал), великого ступеня інтеграції (ВІС – до 10000 елементів на кристал) та надвеликого ступеня інтеграції (НВІС – більш 10000 елементів на кристал). Логічні елементи у вигляді ІС реалізують сукупність простих логічних операцій: І, АБО, І–АБО, І–НЕ, АБО–НЕ і т.д. Логічні елементи на СІС і БІС реалізують вузли ЕОМ, на НВІС – мікроЕОМ.

Основними параметрами серії логічних елементів є:

- живлення напруги і сигналів для представлення логічного 0 і логічної 1-ці;

- коефіцієнти об'єднання входу;

- навантажувальна здатність (коефіцієнт розгалуження по виходу);

- завадостійкість;

- розсіює потужність;

- швидкодія.

Серія елементів характеризується кількістю використовуваних живлячих напруг і їх номінальними значеннями. Зазвичай логічному 0 відповідає низький рівень напруги, а логічній 1-ці – високий. Для найбільш часто використовуваних серій напруга живлення складає + 5В, рівень логічної одиниці 2,4–5В, рівень логічного 0 – 0–0,4В.

Коефіцієнт об'єднання входу (К_ов) визначає максимально можливе число входів логічного елемента, іншими словами, функцію скількох змінних може реалізувати цей елемент. Зазвичай К_ов набуває значення від 2 до 4, рідше К_ов = 8. Збільшення числа входів пов'язано з ускладненням схеми елементів і призводить до погіршення інших параметрів – завадостійкості, швидкодії і т.д.

Коефіцієнт розгалуження по виходу (К_рпв) показує на скільки логічних входів може бути одночасно навантажений вихід даного логічного елемента. Зазвичай, К_рпв для найбільш часто використовуваних серій дорівнює 10. Іноді замість К_рпв задається гранично допустиме значення вихідного струму логічного елемента в стані 0 або 1-ці.

Завадостійкість – це здатність елемента правильно функціонувати за наявністю перешкод. Вона визначається максимально допустимою напругою перешкода, за якої не відбувається збою в його роботі. Зазвичай, це напруга порядку 0,6–0,9 В.

Швидкодія логічних елементів є одним із найважливіших параметрів і характеризується часом затримки поширення сигналу. Цей параметр істотно залежить від технології виготовлення мікросхем і лежить у діапазоні від одиниць до сотень наносекунд.

Найбільш часто вживані типи інтегральних мікросхем – це потенційні елементи транзисторно-транзисторної логіки (ТТЛ) – серії К155, К555, К531, К1533 і т.д., транзисторної логіки з емітерний зв'язками (Естлі) – це серії К500, К1500, елементи на КМОН транзисторах – серії К176, К561, К564 і т.д.

Під час синтезу КС на реальних логічних елементах необхідно обов'язково враховувати обмеження на К_ов і К_рпв.

8.4 Синтез КС з урахуванням обмеження на

Поданням функції у вигляді ДНФ відповідає дворівнева КС (якщо вважати, що на її вхід можуть надходити як прямі, так і інверсні вхідні сигнали), на першому рівні якої елементи І, а їх виходи об'єднуються на другому рівні елементом АБО. Така побудова КС забезпечує її максимальну швидкодію, оскільки ранг схеми мінімальний. Однак, не завжди можливо на першому рівні і, особливо, на другому вибрати логічні елементи з необхідним , тому може виявитися, що ЛЕ з таким не випускаються промисловістю. У цьому випадку необхідно за допомогою декількох елементів із меншим отримати еквівалент із великим або, що краще, перетворити БФ, перейшовши від ДНФ до скороченої форми. Цей перехід супроводжується зменшенням логічних елементів, необхідних для побудови схеми. Здійснити такий перехід можна за допомогою факторного алгоритму, суть якого розглянемо на прикладі.

Нехай задано деяку булеву функцію у вигляді:

. (8.5)

Для реалізації цієї функції за наведеним рядом необхідно використовувати
3 логічних елемента 4І, один логічний елемент 5І, один логічний елемент 4АБО.

За допомогою факторного алгоритму отримаємо дужкову форму для заданої функції. Для цього позначимо всі кон'юнкції буквами: і будемо розглядати їх як деякі множини. Знаходимо попарні перетину множин:, , , , , .

Отримані перетини показують загальні частини окремих кон'юнкцій. Вибираємо перетин, який має найбільшу довжину (якщо таке відсутнє, то вибирають те, яке найчастіше зустрічається). У даному випадку це . Тому з кон'юнкції А і В виносимо загальну частину . Тоді маємо:

. (8.6)

Позначимо F = і знаходимо перетини:

, , . (8.7)

Отже, для вихідної функції маємо:

. (8.8)

Позначимо, , перетин . Отже, остаточно маємо:

. (8.9)

Для реалізації функції за останнім висловом необхідно 5 елементів 2І, 1 елемент 3І, 3 елемента 2АБО (рисунок 8.7).

Як видно з отриманої схеми для її реалізації необхідні елементи з = 2 або 3 (на відміну від вихідної з = 4 або 5). Однак ранг схеми збільшився до 7, що призводить до збільшення затримки спрацьовування схеми.

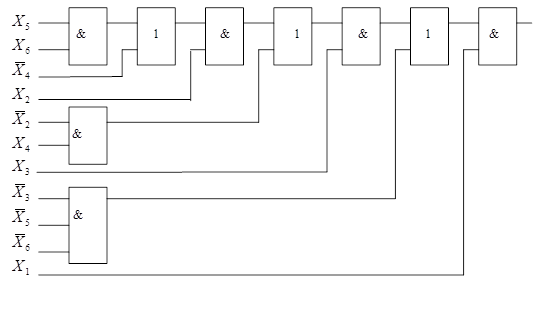
Рисунок 8.7 – Функціональна схема, яка отримана на основі факторного алгоритму

8.5 Аналіз комбінаційних схем

Завдання аналізу КС виникають за необхідністю перевірити правильності синтезу (на етапі проектування) або визначити БФ, реалізовану КС (під час аналізу або ремонту схем). Всі існуючі методи аналізу поділяються на прямі і непрямі.

У результаті аналізу КС прямим методом виходить безліч наборів вхідних змінних, що забезпечують задане значення на виході, що дозволяє записати в алгебраїчному вигляді БФ, реалізовану схему. До прямих методів відноситься метод p- алгоритму.

Застосування непрямих методів дає можливість визначити реакцію схеми на заданий набір вхідних змінних у статиці або проаналізувати перехідний процес зміни одного вхідного набору на інший. Прикладами непрямих методів аналізу, є методи синхронного та асинхронного моделювання.

Всі згадані методи аналізу є машинo-орієнтованими, що дозволяє виконати аналіз схеми на ЕОМ. Для всіх методів аналізу необхідно описати схему у вигляді схемного списку, до якого включаються в загальному випадку такі дані: номер ЛЕ у схемі; логічна функція, реалізована ЛЕ; вхідні змінні для даного ЛЕ.

8.6 Аналіз комбінаційних схем методом p-алгоритму

При цьому методі, як згадувалося вище, шукаються набори вхідних змінних, що забезпечують задане значення на виході КС. Набори, що забезпечують на виході КС логічну 1-цю, утворюють так зване одиничне покриття.

Рисунок 8.8 – Приклад аналізу КС

Аналогічно, вхідні набори, що забезпечують на виході КС логічний 0, утворюють нульове покриття . Розглянемо покриття і для найпростішого логічного елемента 2І, що виконує функцію Y = X₁X₂. Таблиця істинності для цієї функції:

Таблиця 8.3 – Таблиця істинності функції Y = X₁X₂

Як видно з наведеної таблиці тільки при єдиному наборі X₁ = 1 і X₂ = 1 на виході ЛЕ буде 1-ця, тобто одиничне покриття включає тільки один набір = {1 -1}. На виході ЛЕ буде 0 при трьох наборах, що утворюють нульове покриття:

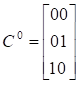. (8.10)

Це покриття можна спростити, зауваживши, що перший набір склеюється з другим і третім, тобто:

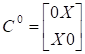. (8.11)

Тобто для ЛЕ 2І можна сказати, що 1-ця на його виході буде тільки при обох одиницях на входах, а для забезпечення 0 на виході достатньо подати хоча б на один вхід 0. Міркуючи аналогічно, отримаємо таблицю покриттів і для основних ЛЕ, представлених нижче у таблиці 8.4.

При аналізі схеми методом p-алгоритму, задавшись певним значенням на виході, замінюють його відповідним покриттям елемента, що формує вихідний сигнал. У результаті цього визначається, які повинні бути сигнали на виходах елементів, підключених до вихідного ЛЕ. У свою чергу, сигнали на виходах цих елементів можна замінити відповідними покриттями, тобто, визначити значення вихідних сигналів для інших ЛЕ і т.д. Цей процес продовжується до тих пір, поки не вийдуть покриття, що складаються тільки з вхідних змінних, званих опорними. Сукупність таких покриттів і дає відповідне покриття схеми.

Таблиця 8.4 – Таблиця станів

ЛЕ Y Y Y Y Y Y Y

НЕ 2І 2І – НЕ 2АБО 2АБО–НЕ ИСК. АБО 3І – НЕ

X X₁ X₂ X₁ X₂ X₁ X₂ X₁ X₂ X₁ X₂ X₁ X₂ X₃

1 0 X 1 1 0 0 1 X 0 0 1 1 1

X 0 X 1 1 1

0 1 1 0 X 1 X 0 0 0 1 0 X X

X 0 X 1 1 0 X 0 X

X X 0

Приклад аналізу КС (рисунок 8.8) методом p-алгоритму представлено в таблиці 8.5. В останній колонці цієї таблиці наведено оператор підстановки, в результаті роботи якого сигнал на виході ЛЕ замінюється відповідним покриттям. Необхідно звернути увагу, що всі значення змінних, записані в одному рядку, повинні одночасно бути в наявності для забезпечення заданого значення вихідного сигналу. Тому, при заміні одного з значень у стрічці відповідним покриттям, всі інші значення для інших змінних у цьому рядку повинні бути присутніми спільно з цим покриттям.

На підставі отриманого одиничного покриття можна записати БФ, реалізовану схемою:

. (8.12)

Таблиця 8.5 – Аналіз схеми методом p- алгоритму

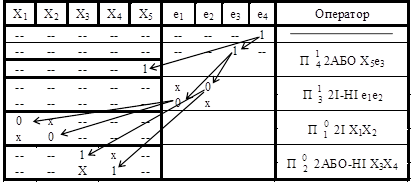
а) Отримання першого покриття

б) Отримання нульового покриття

Надалі можна порівняти отриману БФ з тією, за якою будувалася схема і перевірити правильність її побудови. Під час аналізу схеми може виявитися, що деяка змінна, що отримала на одному з попередніх кроків деякі значення на даному кроці повинна набувати протилежне значення. Суперечність, яка виникла, свідчить про те, що даний шлях є неправильним і його необхідно виключити з подальшого розгляду. Якщо ні за однієї комбінації вхідних змінних не забезпечується значення 1-ця (0) на виході, то це означає, що схема реалізує константу 0 (1) відповідно.

8.7 Аналіз КС-методом синхронного моделювання

При цьому методі вважається, що всі ЛЕ перемикаються одночасно, без затримки. У результаті застосування методу визначається стале значення сигналу на виході схеми.

Розглянемо метод синхронного моделювання на прикладі схеми (рисунок 8.8).

На першому етапі схему розбиваємо на рівні і записуємо в порядку зростання рівня рівняння, що описують функціонування ЛЕ (таблиця 8.6).

Таблиця 8.6 – Функціонування ЛЕ

№ рівня	№ елемента	Рівняння
1	1 2	e₁= X₁ X₂ e₂=
2	3	e₃ =
3	4	Y = e₄ = e₃ + X₅

Проаналізуємо схему при подачі на вхід набору X₁ = 0, Х₂ = 0, Х₃ = 0, Х₄ = 1, Х₅ = 1. Для цього вирішуємо записані рівняння в порядку зростання рівняння. Маємо:

, (8.13)

, (8.14)

, (8.15)

. (8.16)

Отже, при подачі на вхід набору {00011}, на виході буде Y = 1. Аналогічно можна промоделювати роботу схеми при подачі на вхід будь-якого іншого набору.

8.8 Аналіз КС-методом асинхронного моделювання

Реальний ЛЕ перемикається за певний кінцевий час, що залежить від технології виготовлення, умов експлуатації, ємностей навантаження і т.д. Проходження сигналу послідовно через кілька ЛЕ буде призводити до накопичення часу затримки і виникнення зсуву в часі вихідного сигналу у відношенні до вхідного. Наявність затримки і тимчасового зсуву сигналів, може спричинити появу на виході окремих ЛЕ і всієї схеми в цілому короткочасних сигналів, не передбачених БФ, реалізованої схеми. Як ілюстрацію, розглянемо схему (рисунок 8.10, а).

а)

б)

Рисунок 8.10 – Статичний ризик збою: а) – схема; б) – тимчасові діаграми
(t₁ – час затримки інвертора; t₂– час затримки елемента 2І)

Дана схема реалізує функцію, тобто, константу 0 незалежно від вхідного сигналу X. Однак, у перехідному процесі в результаті затримки спрацьовування ЛЕ можлива ситуація, коли на обох входах елемента 2І будуть логічні одиниці, що може призвести до появи на виході схеми логічної 1 (рисунок 8.11, б). Розглянутий випадок можливий у разі затримання спрацьовування другого елемента більше, ніж першого. Таке явище називається ризиком збою. Розрізняють статистичний і динамічний ризики збою.

При статичному ризику у збою до і після перехідного процесу стан вихідного сигналу один і той самий, а під час перехідного процесу можлива короткочасна поява протилежної сигналу.

При динамічному ризику збою до і після перехідного процесу стан вихідного сигналу протилежний, але в перехідному процесі вихідний сигнал кілька разів змінює своє значення. Динамічний ризик збою можливий у схемі (рисунок 8.12, а) на зміну набору (Х₁ = 0, Х₂ = 1, Х₃ = 1) на набір (Х₁ = 1, Х₂ = 0, Х₃ = 0) і ілюструється діаграмами (рисунок 8.11,б).

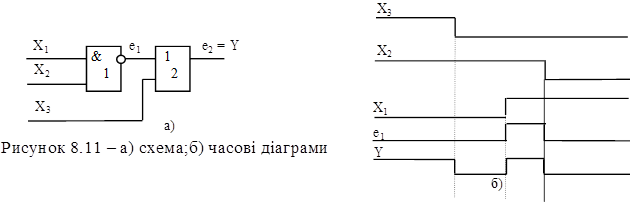
У даному прикладі динамічний ризик збою на виході КС супроводжується статичним на виході елемента 1. Як видно з часових діаграм ризик збою має місце за наявністю певного тимчасового зсуву між сигналами, які надходять на вхід ЛЕ. Небажані сигнали на виході можуть бути і відсутніми за іншого співвідношення часових сигналів, однак принципова можливість їх появи є чинником, який знижує надійність роботи схеми. Тому дуже важливо вміти виявляти і усувати такі явища.

Для аналізу процесу перемикання КС за зміни вхідних наборів і виявлення ризиків збою використовується метод асинхронного моделювання. При цьому методі вважається, що кожен елемент перемикається з однаковою затримкою. Аналіз включає такі етапи:

1. Кожному елементу схеми присвоюється рівень, причому рівень 1-цю мають елементи, всі входи яких є незалежними входами схеми.

2. Записуються рівняння, що описують кожен ЛЕ в порядку убування рівня.

3. Для початкового вхідного набору А (X₁, X₂, ..., X_n) визначається значення сигналів на виходах всіх ЛЕ схеми. Нехай даний набір А замінюється набором В (X₁, X₂, ..., X_n).

4. Виділяються ті рівняння, в правій частині яких хоча б одна з змінних змінила своє значення.

5. Вирішуються помічені рівняння в порядку їх запису в схемі. Після рішення рівняння вважається непомічені.

6. Якщо після вирішення всіх рівнянь системи змінні, що входять у ліві частини рівнянь, змінили свої значення, то знову позначаються ті рівняння, в праві частини яких входять ці змінні. Потім здійснюється перехід до п. 5. У іншому випадку моделювання даного вхідного набору вважається закінченим. Виконання п. 5 називається тактом моделювання.

Аналіз схеми (рисунок 8.12) методом асинхронного моделювання наведено нижче. Для даної схеми вхідний набір А (1011110) замінюється набором В (1101011).

Рисунок 8.12 – Комбінаційна схема для методу асинхронного моделювання

Як випливає з результатів моделювання, при зміні набору А набором В на виході елемента 4 має місце статичний ризик збою, а на виході схеми – динамічний ризик збою.

Радикальним способом усунення ризиків збою є введення стробування для зняття вихідного сигналу КС. Стробуючий імпульс подається після закінчення перехідного процесу в КС (тобто, коли на виході КС вже встановилося необхідне значення вихідного сигналу), що виключає вплив можливих збоїв на сигнал, який виробляється схемою.

Рівняння, що описують ЛЕ (таблиця 8.8).

Таблиця 8.8 – Рівняння, що описують логічні елементи

1-й такт

2-й такт

3-й такт

Y= e₆= e₄+ e₅+ X₅

e₅= e₃ X₇

e₃=X₅ X₆

e₂=X₅ X₄

e₁=X₁ X₂

Таблиця 8.9 – Таблиця моделювання схеми

Виходи Такти моделювання Прик.

0 1 2 3

e₆ 1 0 1 0 дин.

e₅ 0 1 0 0 стат.

e₄ 0 0 0 0

e₃ 1 0 0 0

e₂ 1 0 0 0

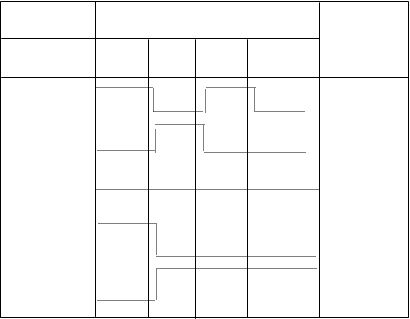
e₁ 0 1 0 1