Самостійна робота №6
Парна Лінійна регресія
Мета
роботи -
придбання навичок апроксимації множини статистичних параметрів рівнянням лінійної регресії різними методами.
Завдання
для самостійного розв’язання
Нехай задана таблиця замірів часу на обслуговування клієнтів в супермаркеті
в залежності від кількості товарів в їх кошиках:
-
визначити коефіцієнт кореляції між факторними і
результативними змінними, зробити висновок про тісноту зв’язку між ними.
-
знайти рівняння лінійної регресії залежності часу
обслуговування клієнта від кількості товару різними способами.
-
порівняти отримані регресійні моделі, обчисливши для
кожної величину відхилень теоретичних значень функції від табличних даних ![]() .
.
Кількість товарів, шт. |
Час на обслуг. с |
Кількість товарів, шт |
Час на обслуг. с |
Кількість товарів, шт |
Час на обслуг. с |
|
10 |
56 |
1 |
20 |
1 |
30 |
|
6 |
65 |
7 |
29 |
1 |
55 |
|
10 |
55 |
16 |
79 |
7 |
149 |
|
41 |
142 |
1 |
12 |
39 |
238 |
|
1 |
32 |
22 |
135 |
13 |
60 |
|
52 |
142 |
7 |
35 |
28 |
95 |
|
9 |
66 |
9 |
65 |
1 |
23 |
|
20 |
305 |
12 |
88 |
42 |
133 |
|
23 |
106 |
3 |
50 |
6 |
50 |
|
3 |
27 |
38 |
171 |
1 |
39 |
|
3 |
53 |
16 |
129 |
9 |
46 |
|
4 |
52 |
12 |
74 |
12 |
82 |
По виду знайденої лінійної залежності ![]() робимо висновки:
робимо висновки:
а – вказує на час
(секунди), які затрачуються на сканування штрих-коду одного товару;
b – час, який йде
на отримання готівки за покупку чи опрацювання кредитної картки клієнта. Також
сюди може входити пакування працівником супермаркету товарів, куплених
клієнтом.
З цього випливає, що мінімальний час обслуговування
одного клієнта з одним товаром складає ![]() , с. (Отримані дані є усередненими).
, с. (Отримані дані є усередненими).
Приклад
розв’язання
1.Визначення
тісноти лінійного взаємозв’язку між вхідними і вихідними даними системи за
допомогою кореляційно-регресійного аналізу.
Нехай деяка парна залежність результативної величини від факторної задана
таблицею значень для n дослідів.
Таблиця 1
|
№ досліду |
1 |
2 |
… |
N |
|
Вхідна
величина |
Х1 |
Х2 |
… |
Хв. |
|
Вихідна
величина |
Y1 |
Y2 |
… |
Yn |
Припустимо існування лінійної залежності між вхідними і вихідними змінними:
![]() .
.
Для виявлення сили взаємозв’язку між вхідними і вихідними параметрами в обчислюється парний коефіцієнт лінійної кореляції.
Використовуючи MS Excel за допомогою спеціальної функції КОРРЕЛ (меню Статистичні функції) з
параметрами:
- Масив 1 – масив вхідних даних;
-
Масив 2 – масив вихідних даних
отримуємо
значення коефіцієнта кореляції R в межах від 0 до ±1.
|
Величина
коефіцієнта кореляції |
Характер
зв’язку |
|
до
± 0,3 |
Практично
відсутній |
|
±
0,3 - ± 0,5 |
Слабкий |
|
±
0,5 - ± 0,7 |
Помірний |
|
±
0,7 - ± 1,0 |
Сильний |
2.
Визначимо параметри рівняння регресії ![]() теоретично і засобами MS Excel.
теоретично і засобами MS Excel.
2.1.
Для розрахунку параметрів a i b вибраної емпіричної функції скористаємося методом
найменших квадратів МНК і методом двох точок.
- Для знаходження коефіцієнтів a i b методом найменших квадратів необхідно
скласти систему рівнянь часткових похідних по незалежних змінних a i b функції
суми квадратів різниць значень функції і табличних даних. Для нашого випадку -
розв’язати систему двох рівнянь:
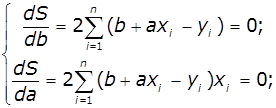
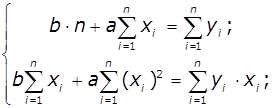
Підставивши значення ![]() знайдемо значення
коефіцієнтів лінійної залежності a i b. Запишемо
вираз для лінійної залежності
знайдемо значення
коефіцієнтів лінійної залежності a i b. Запишемо
вираз для лінійної залежності ![]() .
.
2.2. Для знаходження коефіцієнтів a i b методом двох точок необхідно на
заданому відрізку змінних ![]() обрати дві
точки, які достатньо надійні і, за можливістю, далеко розташовані одна від
одної, наприклад, крайні точки з координатами
обрати дві
точки, які достатньо надійні і, за можливістю, далеко розташовані одна від
одної, наприклад, крайні точки з координатами ![]() і
і ![]() і скласти систему 2 рівнянь
підставивши значення даних точок в вибрану функцію
і скласти систему 2 рівнянь
підставивши значення даних точок в вибрану функцію ![]() :
:
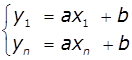
В результаті розв’язання
отримаємо апроксимуючу функцію ![]() .
.
2.3. Порівняємо точність визначення коефіцієнтів апроксимуючої функції
двома методами. Знайдемо відхилення значень теоретичних функцій ![]() і
і ![]() від табличних значень
обрахувавши суму квадратів відповідних різниць:
від табличних значень
обрахувавши суму квадратів відповідних різниць:
![]() ,
, ![]()
При меншому значенні абсолютної похибки функція краще відображає вихідні
дані задачі. Для наочності зобразити графіки вхідних даних і обох функцій ![]() і
і ![]() .
.
2.4. Для таблиці даних, що
описують деякий процес і представлених діаграмою, у MS Excel є ефективний
інструмент регресійного аналізу – додавання лінії тренду до графіка залежності
результативних даних від факторних, що дозволяє:
-
будувати на основі
методу найменших квадратів і додавати в діаграму п'яти типів регресій, що з тим чи іншим ступенем точності моделюють
досліджуваний процес;
-
додавати до діаграми рівняння
побудованої регресії;
-
визначати ступінь
відповідності обраної регресії відображуваним на діаграмі даним.
Покажемо
наявність взаємозв’язоку між масивами xі та yі у вигляді графіка, для чого
використаємо «Мастер диаграмм – Тип –
Точечная».
Для того, щоб на графіку додати лінію
регресії, необхідно поставити курсор на будь-яку точку графіка та натиснути
праву кнопку миші. У меню, яке після цього з’являється на екрані, обрати
команду «Добавить линию тренда».
У діалоговому вікні вибрити тип «Линейная», зайти в
підменю «Параметры» та відмітити команду «показывать уравнение на диаграмме».
В результаті на графіку буде зображено кореляційне поле, лінію регресії та
виведено лінійне рівняння регресії.
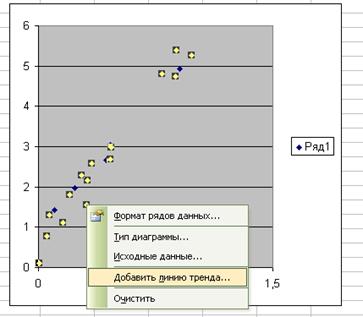
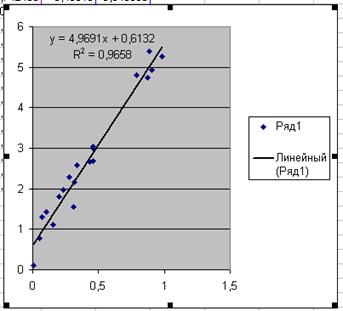
Рис 1. Визначення рівняння регресії за допомогою трендів.
2.5. Для реалізації процедури регресія в
MS Excel (2007+) існує пакет функцій регресійного аналізу даних.
Для розв’язання завдання обираємо у
меню «Сервис» пакет «Анализ
данных» та інструмент аналізу «Регрессия»,
параметрами якого є масиви факторного і результативного показника xі та yі.
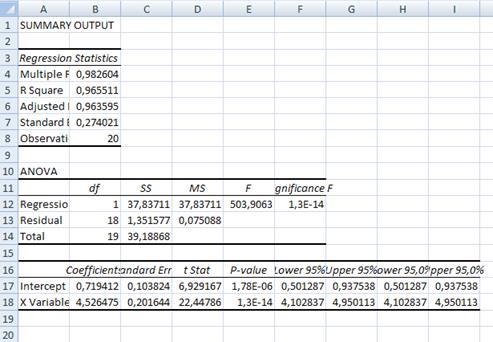
Рис.2.Розрахунок
параметрів регресійно-кореляційного аналізу.
Результати
регресійного аналізу показані на рис.2. Тут розраховані наступні дані:
-
коефіцієнти регресії (на рис. комірки В17, В18) ![]() ;
;
-
лінійний коефіцієнт кореляції (А4) R=0,98;
-
коефіцієнт детермінації (А5)![]() (показує що зміна y
зумовлюється зміною х на 96%);
(показує що зміна y
зумовлюється зміною х на 96%);
-
стандартна помилка (А7) = 0,27;
-
кількість спостережень (А8) =20;
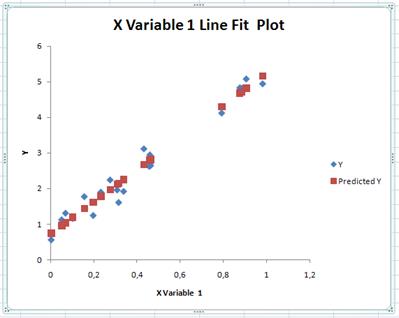
Рис.3. Графік вхідних значень результативного фактору y
та передбачених значень згідно рівняння регресії.
Контрольні
запитання
1.
Завдання кореляційного і регресійного
аналізу.
2.
Апроксимація і інтерполяція
досліджуваних даних.
3.
Встановлення тісноти зв’язку між
змінними за допомогою коефіцієнта кореляції.
4.
Розрахунок параметрів рівняння
лінійної регресії методом МНК.
5.
Розрахунок параметрів рівняння
лінійної регресії методом двох точок.
6.
Як можна оцінити точність
апроксимуючої функції?
7.
Визначення рівняння регресії за
допомогою трендів в MS Excel.