Самостійна робота №5
Ідентифікація закону розподілу
Мета.
Навчитись ідентифікувати закон розподілу випадкових параметрів системи.
Завдання
для самостійного розв’язання
Задача 1. Результати вимірювання діаметрів 200 деталей після шліфування подано в
таблиці.
Частотний
варіаційний ряд діаметрів деталей
|
і |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
xi,
мм |
6,69 |
6,7 |
6,71 |
6,72 |
6,73 |
6,74 |
6,75 |
|
Ni |
3 |
12 |
6+N/3 |
11 |
14+N/2 |
30 |
25+N |
|
і |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
xi,
мм |
6,76 |
6,77 |
6,78 |
6,79 |
6,8 |
6,81 |
6,82 |
|
Ni |
27+N |
31 |
14+N/2 |
8 |
5+N/3 |
6 |
5 |
Необхідно:
1)
визначити основні числові характеристики ряду;
2)
побудувати гістограму емпіричного розподілу;
3)
побудувати теоретичну криву нормального розподілу і перевірити відповідність
емпіричного і теоретичного розподілів по критерію Пірсона. (рівень значимості a
= 0,05)
Задача
2. На одній з міських АТС фіксувалася кількість
телефонних дзвінків в годину. Спостереження велися на протязі 100 годин, їх
результати представлені в таблиці. Чи можна вважати навантаження на АТС
стандартним?
|
Кількість викликів в годину |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Кількість спостережень |
6 |
27 |
26 |
20 |
10 |
5 |
5 |
1 |
Зауваження. Навантаження на АТС можна вважати стандартним, якщо
випадкова величина Х – кількість
телефонних дзвінків, що поступили, підкоряється закону розподілу Пуассона.
Тобто отримання відповіді необхідно перевірити гіпотезу про
закон розподілу випадкової величини.
Задача
3. З метою впорядкування роботи міського суспільного
транспорту фіксувався час очікування в хвилинах пасажирами тролейбусів на
декількох маршрутах. Було проведено 200 вимірювань, їх результати представлені
в таблиці. Чи можна вважати, що перевезення по перевірених маршрутах
забезпечені раціонально?
|
Час очікування, хв |
1 – 3 |
3 – 5 |
5 – 7 |
7 – 9 |
9 – 11 |
11 – 13 |
|
Кількість спостережень |
25 |
30 |
48 |
35 |
42 |
20 |
Зауваження. Можна вважати, що перевезення по перевірених маршрутах
забезпечені раціонально, якщо випадкова величина Х – час очікування пасажирами транспорту підкоряється рівномірному
закону розподілу. Тобто задача зводиться до перевірки гіпотези про закон
розподілу випадкової величини.
Задача 4. Статистичними
спостереженнями встановлено, що у автомобіля КрАЗ-6510 лампочки покажчиків
повороту перегоріли на пробігу (тис. км):
8,3; 18,4; 27,8; 47,1; 74; 19,7; 3; 11,8;
17,4; 14; 9,7; 34,1; 4; 31,9; 42; 7,3; 85,2; 39,6; 53; 57; 21,8; 58,4; 38,1.
Потрібно:
1. Встановити закон, якому
підпорядковується досліджуване явище, розрахувати і побудувати теоретичну криву
частот відмови лампочок.
2. Перевірити правдоподібність
зробленої гіпотези за критерієм згоди Пірсона при рівні значущості a
= 0,05.
Задача
5. В сервісному центрі на протязі 100 днів фіксували
щоденну кількість заявок. Результати спостережень представлені в таблиці. Чи
можна вважати розподіл заявок нормальним?
|
Кількість заявок в день |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
|
Частота |
4 |
5 |
24 |
19 |
26 |
21 |
2 |
1 |
Задача 6.
Проведено сто вимірювань деякої випадкової величини. Побудувати гістограму,
висунути гіпотезу про закон розподілу, перевірити на скільки вона узгоджується
з експериментом.
|
Інтервали значень |
0 - 2 |
2 - 4 |
4- 6 |
6 - 8 |
8 - 10 |
10 - 12 |
|
Частота попадань |
3 |
16 |
28 |
32 |
14 |
7 |
Задача
7.
Час роботи деталі до відмови приведений статистичним рядом див. таблиця. Перевірити гіпотезу про те, що час
роботи розподілений по показниковому (експоненційному) закону.
|
Інтервали часу |
0 - 5 |
5 - 10 |
10- 15 |
15 - 20 |
20 - 25 |
25 - 30 |
|
Число елементів |
133 |
45 |
15 |
4 |
2 |
1 |
Задача 8.
Для вивчення транспортного потоку на шосе провели підрахунок числа автомобілів
за 100 хв. Встановити вид закону розподілу даних.
|
Число автомобілів |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Кількість хв |
14 |
33 |
21 |
14 |
9 |
7 |
2 |
Задача
9.
Проведено вимірювання відхилення деталей від стандарту. Перевірити гіпотезу про
те, що відхилення розподілені по нормальному закону.
|
Границі відхилень, мк |
-30.. -20 |
-20.. -10 |
-10..0 |
0..10 |
10..20 |
20..30 |
|
Число деталей |
1 |
12 |
37 |
32 |
14 |
4 |
Задача
10.
Для дослідження потоку заявок в системі масового обслуговування підрахували
число заявок за 100 хв. Перевірити гіпотезу про те, що дані про кількість
хвилин з заявками розподілені по закону Пуассона.
|
Число заявок за
хвилину |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 і більше |
|
Число хвилин |
19 |
21 |
31 |
12 |
8 |
5 |
4 |
0 |
Приклад виконання завдання:
1. Згенерувати
ряд випадкових чисел по заданому закону. Сортувати ряд в порядку зростання.
|
Інтервали [Хі,
Хі+1) |
Середина
інтервалу, Х*і |
Частота
попадання ni |
Відносна
частота ωі=ni
/n |
Густина
частот ωі/h |
|
|
|
|
|
|
2. Розбити
ряд на k інтервалів, підрахувати число попадань в кожен інтервал. Побудувати
гістограму розподілу частот.
3. По
виду гістограми частот зробити припущення про вид закону розподілу. Провести
оцінку значення математичного очікування і середньоквадратичного відхилення для
цього закону розподілу:
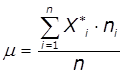 ,
, 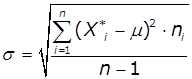
4. Побудувати
теоретичну інтегральну криву розподілу ![]() використовуючи пакет
стандартних функцій MS Excel.
використовуючи пакет
стандартних функцій MS Excel.
НОРМРАСП(x;среднее;стандартное_откл;интегральная)
- функція для нормального закону розподілу;
ЭКСПРАСП(x;лямбда
;интегральная) – функція експоненційного розподілу;
ГАММАРАСП(x;альфа
;бета ;интегральная) – функція гамма розподілу;
ЛОГНОРМРАСП(x;среднее;стандартное_откл) – інтегральний логарифмічний ормальний
рзподіл х, де lnx – нормально розподілена величина;
ПУАССОН(x;среднее;интегральная)
– розподіл Пуассона.
де
x — значення,
для якого знаходиться теоретична імовірність появи – середина кожного інтервалу
з гістограми частот;
Среднее —
середнє арифметичне розподілу;
Стандартное_откл —
стандартне (середньоквадратичне) відхилення;
Интегральная —
логічне значення, що визначає форму функції. Якщо ИСТИНА, то результатом
буде інтегральна функція розподілу, якщо ЛОЖЬ – то функція густини розподілу.
5. Розрахувати
імовірність появи величини в кожному з інтервалів ![]()
6. Здійснити
перевірку гіпотези за критерієм Пірсона:
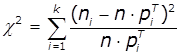
|
Інтервали
спостережень [Хі, Хі+1) |
Спостережувана
частота попадання ni |
Імовірність
попадання в інтервал рі |
Очікувана
теоретична частота nрі |
Доданки
критерію |
|
|
|
|
|
|
|
Всього |
|
|
|
|
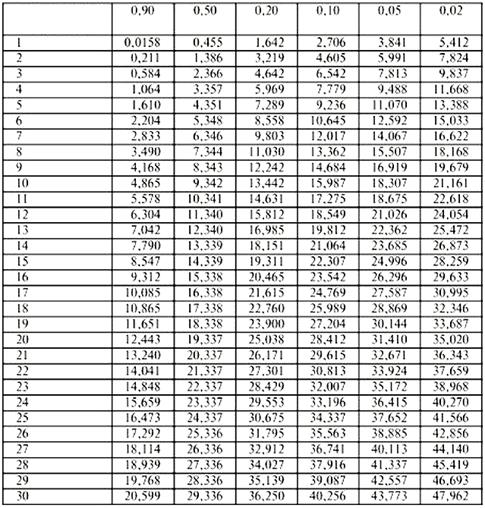
7. Порівняти
розраховане значення ![]() з табличним. Зробити
висновок про правильність прийнятої гіпотези про закон розподілу.
з табличним. Зробити
висновок про правильність прийнятої гіпотези про закон розподілу.
Контрольні
запитання
1. Основні
числові характеристики статистичних рядів.
2. Наведіть
приклади найпоширеніших законів розподілу випадкових величин.
3. Етапи
ідентифікації закону розподілу величини.
4. Побудова
гістограми частот.
5. Перевірка
відповідності експериментальних даних вибраному закону розподілу. Критерій
Пірсона.

