Самостійна робота №7

Багатофакторна і нелінійна регресія

Мета роботи - отримання навичок апроксимації множини статистичних параметрів рівняннями нелінійної регресії.

Завдання для самостійного розв’язання

1. Забудовник оцінює вартість групи офісних будівель в традиційному діловому районі міста. При цьому відому наступні вихідні дані

Ціна будівлі, $	Загальна площа, м²	Кількість офісів	Кількість входів	Час експлуатації, роки
142 000	2310	2	2	20
144 000	2333	2	2	12
151 000	2356	3	1,5	33
150 000	2399	3	2	43
139 000	2402	2	3	53
179 000	2425	4	2	23
126 000	2448	2	1,5	99
142 900	2451	2	2	34
163 000	2494	3	3	23
179 000	2417	4	4	55
149 000	2540	2	3	22

Висунули припущення, що існує множина лінійна залежність ціни будівлі від площі, кількості офісів, кількості входів, часу експлуатації.

Необхідно:

1. Побудувати множину регресійну модель.

2. Оцінити коефіцієнти кореляції та детермінації, стандартну помилку, дати пояснення отриманим результатам.

3. Провести F-тест та t-тест, дати пояснення отриманим результатам.

2. Маємо часовий ряд – Офіційний курс гривні до 100$ США, встановлений Національним банком України, середній за період з 2005 по 2015рр. Визначити, який вид функції найкраще підходить для опису тренду заданого часового ряду. Зробити прогноз на наступний рік.

2005	2006	2007	2008	2009	2010
512,47	505,00	505,00	526,72	779,12	793,56

2011	2012	2013	2014	2015	2016	2017
796,76	799,10	799,30	1188,67	2184,47	2591.18	2712,56

3. Дана динаміка зміни цін на паливо марки А 95, грн./л за місяць липень вказаного року. Визначити, який вид функції найкраще підходить для опису тренду заданого часового ряду. Зробити прогноз на наступний рік.

2005	2006	2007	2008	2009	2010	2011
3,35	3,85	3,98	6,36	6,77	7,74	10,34

2012	2013	2014	2015	2016	2017
10,80	10,91	15,37	20,03	22,32	24,59

За умовами задач 2 і 3 встановити вид залежності між курсом гривні до долара і ціною на бензин в Україні від 2005 по 2017рр. Оцінити коефіцієнт кореляції між даними.

2. Зміни чисельності населення в Україні та місті Києві по роках відображена в таблиці. Визначити оптимальні рівняння регресії для двох графіків. Записати прогноз кількості населення на 2020р.

Рік	1990	1992	1994	1996	1998	2000
Україна	51 838,5	52 056,6	52 114,4	51 297,1	50 370,8	49 429,8
м. Київ	2 624,4	2 651,3	2 653,5	2 638,7	2 629,3	2 631,9

2002	2004	2006	2008	2010	2012	2014	2016
48 457,1	47 622,4	46 929,5	46 372,7	45 962,9	45633,6	45 426,2	42 760,5
2 611,3	2 639,0	2 693,2	2 740,2	2 785,1	2 814,3	2 868,7	2 906,6

Приклад розв’язання

1. Для реалізації процедури множинної (багатофакторної) регресії в MS Excel (2007+) обираємо у меню «Сервис» пакет «Анализ данных» та інструмент аналізу «Регрессия», параметрами якого є масиви і результативного показника. В результаті отримаємо модель множинної лінійної регресії по параметрах х_і , а також:

- коефіцієнт множинної кореляції R – показує тісноту зв’язку вихідної змінної від вхідних;

- коефіцієнт детермінації R² – показує наскільки вихідна змінна, яка визначена на основі побудованої моделі відповідає реальним даним. Якщо R²близький до 0, то це означає низьку значимість моделі, відсутні лінійна залежність між параметрами.

- стандартна помилка - показує середню величину відхилення вихідної змінної y*, яка обрахована на основі моделі, від наявних статистичних значень вихідної змінної y.

- F-тест та t-тест проводять для оцінки значущості моделі. Для цього використовують порівняння так званих фактичних та табличних (теоретичних) значень F-критерію (критерій Фішера) та t-критерію (критерій Стьюдента).

t-тест (або t-критерій) досліджує лінійну залежність між кожною окремою вхідною змінною (Xi) і вихідною змінною (Y), F-тест (або F-критерій) досліджує лінійну залежність для всієї моделі, тобто між НАБОРОМ вхідних змінних (X1, X2,..., Xn) та вихідною змінною (Y) рис.1.

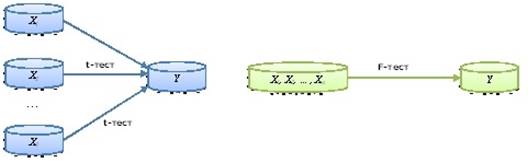
Рис.1. Пояснення критерію Фішера та Стьюдента.

Табличні (критичні) значення F-критерію можна визначити або зі спеціальної таблиці, або за допомогою функції FРАСПОБР в Excel:

1. Стаємо в будь-яку комірку.

2. Запускаємо функцію FРАСПОБР і задаємо:

· «Вероятность» – 0,05

· «Степени_свободы1» – m (m – кількість вхідних змінних X_i).

· «Степени_свободы1» – n-m-1 (n – кількість спостережень).

Якщо, F_факт>F_табл, то між усіма вхідними змінними в цілому та вихідною змінною існує лінійна залежність. Також кажуть, що лінійна модель є значущою.

В t-тесті потрібно співставити фактичні t-критерії та критичний (табличний) t-критерій. Якщо |t_факт|>t_критдля конкретної змінної, то кажуть, що змінна статистично значуща або між даною змінною та вихідною змінною існує лінійний зв’язок.

Обчислення t_крит можна робити за допомогою спеціальних таблиць або функції СТЬЮДРАСПОБР.

Стаємо у будь-яку комірку і запускаємо функцію СТЬЮДРАСПОБР:

- «Вероятность» – 0,05

- «Степени_свободы» – n-m-1 (n – кількість спостережень, m – кількість вхідних змінних X_i).

В результаті отримуємо, що t_крит і порівнюємо з t_фактдля кожної окремої змінної Хі..

2. Для знаходження нелінійного однофакторного рівняння регресії, необхідно побудувати точковий графік по заданих факторних і результативних даних (хі, yi) , поставити курсор на будь-яку точку та натиснути праву кнопку миші. У меню, яке після цього з’являється на екрані, обрати команду «Добавить линию тренда». У діалоговому вікні вибрати тип лінії тренду:

- лінійна;

- логарифмічна

- поліноміальна (вибрати степінь полінома)

- степенева

- експоненційна.

В підменю «Параметры» відмітити команду «показывать уравнение на диаграмме» та «поместить на диаграму величину достоверности аппроксимации (R^2)». На графіку отримаємо вид рівняння регресії і значення коефіцієнта детермінації рис.1.

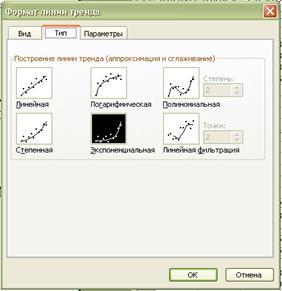
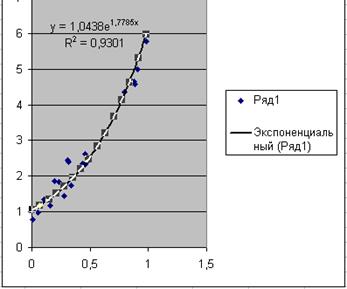
Рис.1. Визначення рівняння нелінійної регресії в функції «Лінія тренду»

Підставивши в отримане рівняння значення факторного параметра хі отримаємо теоретичні значення залежної змінної . Порівняти якість отриманої моделі з різними типами ліній регресії можна порівнявши суми квадратів відхилень результативних даних і теоретичних, отриманих з рівняння регресії : менше значення відхилень показує кращу якість апроксимації.

Контрольні запитання

1. Одно- і багатофакторна регресійна залежність.

2. Лінійна і нелінійна регресійна залежність.

3. Вибір виду функції регресії.

4. Зведення нелінійних апроксимуючих функцій до лінійного вигляду.

5. Застосування методу МНК для побудови множинної лінійної регресії.

6. Оцінка F-тесту множинної кореляції.

7. Оцінка t -тесту множинної кореляції.

8. Визначення рівняння нелінійної регресії за допомогою трендів.

9. Порівняння якості різних типів ліній регресії.