Практична робота № 9

Графічне моделювання Систем масового обслуговування

Мета: навчитися будувати і аналізувати структурні схеми систем масового обслуговування.

Основні теоретичні відомості

Система масового обслуговування (СМО) – це системи виробництва, обслуговування, управління, в яких однорідні події повторюються багато разів, наприклад, на підприємствах побутового обслуговування; у системах прийому, переробки і передачі інформації; автоматичних лініях виробництва і ін. Основні елементи СМО – це об’єкти, що обслуговуються в СМО (вимоги чи заявки), та один або декілька обслуговуючих пристроїв з чергою. У відкритій мережі МО вимоги надходять ззовні мережі і після обробки залишають її. У закритій мережі МО деяка кількість вимог весь час знаходиться в ній, переходячи з однієї СМО до іншої, але ніколи не залишаючи мережу МО.

Мережі масового обслуговування функціонують за наступними простими правилами:

1. Вимоги, що надходять на обслуговування, проходять одну за одною СМО згідно указаного маршруту.

2. На вході кожної СМО вимога намагається знайти один вільний пристрій з декількох паралельно функціонуючих. Правило, за яким вимога обирає той чи інший пристрій за умови, що вони вільні, може бути указано окремо у відповідності до процесу функціонування реальної системи. Якщо всі пристрої однакові, то вимога переглядає пристрої по порядку і займає перший, що виявився вільним.

3. Якщо в момент надходження вимоги до СМО всі пристрої виявились зайнятими, то вимога при наявності черги у СМО намагається в неї потрапити, або залишає мережу масового обслуговування і вважається не обслугованою.

4. Черга у СМО обов’язково одна. Кількість місць у черзі може бути обмежена або необмежена. Якщо в реальному процесі не виникає проблеми з наявністю вільного місця у черзі, то при моделюванні така черга може вважатись необмеженою, навіть якщо місць у ній декілька. Отже, обмеження на кількість місць у черзі вводять, коли потрібно моделювати ситуацію „в даний момент вимога не може бути прийнята у СМО”.

При графічному представленні мережі МО користуються наступними позначеннями:

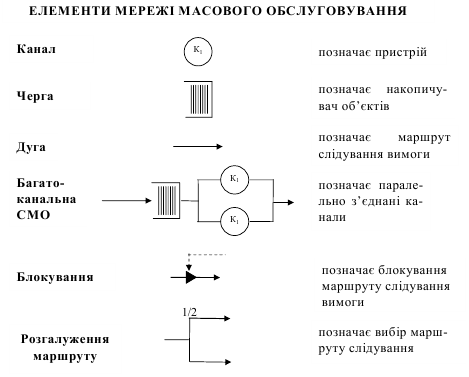
Мережа масового обслуговування може мати такі ускладнюючі елементи, як декілька типів вимог, що обслуговуються, розгалуження та блокування маршрутів, черги із складними правилами упорядкування вимог у них, тощо.

· Декілька типів вимог вводять у разі, якщо потрібно розрізняти час обслуговування у пристроях для різних типів вимог, або маршрути слідування (у тому числі ймовірності слідування від однієї СМО до іншої).

· Розгалуження маршруту означає, що маршрут вимоги може бути визначений тільки з певною ймовірністю. Сума ймовірностей у місці розгалуження маршруту складає одиницю.

· Блокування маршрутів допомагають ввести в мережу МО елементи, що управляють процесом обслуговування. Наприклад, вилучити поламаний пристрій з процесу обслуговування, заборонити подальше просування вимоги до виконання деякої умови, тощо.

· Черги із складними правилами упорядкування розглядаються у випадках, коли потрібно установити пріоритети обслуговування вимог в залежності від, наприклад, типу вимоги, накопленого часу обслуговування вимоги і т.і.

Для того, щоб представити систему засобами мережі масового обслуговування потрібно:

- з’ясувати, що являється в системі об’єктом обслуговування;

- виділити елементи процесу обслуговування об’єктів і кожному елементу поставити у відповідність СМО;

- для кожної СМО визначити кількість пристроїв та наявність черги;

- з’єднати СМО у відповідності до процесу обслуговування;

- визначити маршрут проходження об’єкту обслуговування від однієї СМО до іншої;

- визначити умови надходження в кожну СМО (ймовірність вибору маршруту);

- визначити наявність блокування маршруту та умови блокування;

- визначити числові значення параметрів кожної СМО;

- визначити числові значення параметрів зовнішнього потоку на обслуговування;

- визначити стан мережі масового обслуговування на початку моделювання.

Приклад графічного представлення СМО

Приклад 1. Розглянемо, наприклад, функціонування мережі МО, яка представлена на рисунку 1.

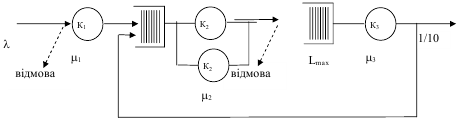
Рис.1. Приклад мережі масового обслуговування.

Усі об’єкти проходять три етапи обробки – СМО1, СМО2, СМО3.

До першої СМО об’єкти надходять на обслуговування з інтенсивністю λ (вимог/од. часу), де обслуговуються пристроєм К1 з інтенсивністю μ1 (вимог/од. часу). Оскільки в першій СМО відсутня черга, то об’єкти, що надійшли в момент часу, коли пристрій зайнятий, отримують відмову в обслуговуванні і вважаються не обслугованими мережею МО.

Ті об’єкти, що пройшли обслуговування у першому пристрої мережі МО надходять до другої СМО. У другій СМО об’єкти обслуговуються в одному з каналів обслуговування К2. Якщо в момент надходження об’єкта до другої СМО обидва канали зайняті, об’єкт надходить до черги другої СМО. Обмеження на довжину черги другої СМО не указане, тому кількість об’єктів, що одночасно знаходяться в цій черзі, може бути будь-якою. Коли закінчилось обслуговування вимоги в одному з каналів другої СМО об’єкт намагається потрапити до третьої СМО. Об’єкт потрапляє на обслуговування в канал третьої СМО, якщо він вільний, в іншому випадку він намагається зайняти місце в черзі третьої СМО. Але черга третьої СМО має обмежену кількість місць Lmax. Це означає, що об’єкт, який намагається потрапити до черги третьої СМО у момент, коли всі місця в ній зайняті, отримує відмову в обслуговуванні.

Об’єкт, який закінчив обслуговування у каналі третьої СМО, з імовірністю 1/10 повертається до другої СМО для додаткової обробки і з імовірністю 9/10 виходить з мережі МО як успішно обслугований. Такі повернення на додаткову обробку зустрічаються, наприклад, у системах з пунктами контролю якості: з імовірністю 9/10 об’єкт проходить перевірку якості успішно і з імовірністю 1/10 в результаті перевірки виявляється, що об’єкт неякісний і потребує додаткової обробки.

Блокування маршруту може здійснюватись з різних причин і може відноситись до різних елементів мережі МО. Наприклад, канал обслуговування блокується, якщо наступний канал обслуговування зайнятий і зайняті всі місця в його черзі. Або, за умови перевищення кількості вимог в черзі основного каналу, блокування резервного каналу знімається. Умова блокування може бути задана також за станом не одного, а декількох елементів мережі МО, і взагалі може бути будь-якою складною.

Мережа масового обслуговування, розглянута на рис 1, має дві точки, де вимога, що обслуговується, може отримати відмову.

Перша – на початку процесу обслуговування, і друга - коли вимога, яка завершила обслуговування у другій СМО і намагається потрапити до третьої СМО у момент, коли всі місця у її черзі зайняті позначається блокуванням маршруту слідування вимоги. Вимога очікує звільнення місця у третій СМО у тому пристрої, в якому завершила обробку.

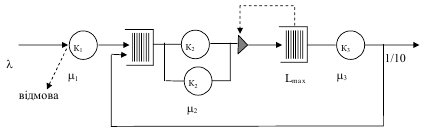
Рис. 2. Приклад ММО з блокуванням маршруту.

Наприклад, у робототехнічних системах робот, що закінчив обробку деталі і не знаходить місце, куди покласти оброблену деталь, змушений тримати її до тих пір, поки місце для деталі звільниться.

Отже, специфічний стан пристрою, коли з одного боку він зайнятий вимогою, оскільки вимога займає місце обробки, з іншого боку – пристрій вільний, оскільки він не виконує роботу по обробці вимоги, називається блокуванням. Блокування маршруту означає, що маршрут слідування вимог у вказаному місці закритий і вимога не може слідувати по цьому маршруту до моменту, коли блокування маршруту буде знято.

Приклад 2. Складіть формалізовану модель системи масового обслуговування для наступної задачі:

Система передачі даних забезпечує передачу пакетів даних із пункту А в пункт С через транзитний пункт В. У пункті А пакети надходять через 10±5 мс. Тут вони буферуються в накопичувачі ємністю 20 пакетів і передаються по будь-якій із двох ліній АВ1- за час 20 мс або АВ2- за час 20±5 мс.

У пункті В вони знову буферуються в накопичувачі ємністю 25 пакетів і далі передаються по лініях ВС1 (за 25±3 мс) і ВС2 (за 25 мс). Причому пакети з АВ1 надходять у ВС1, а з АВ2 - в ВС2. Щоб не було переповнення накопичувача, у пункті В вводиться граничне значення його ємності - 20 пакетів.

При досягненні чергою граничного значення відбувається підключення резервної апаратури і час передачі знижується для ліній ВС1 і ВС2 до 15 мс.

Метою моделювання є визначення ймовірності підключення резервної апаратури, відсотку пакетів, які не передались через завантаження ліній зв’язку, та статистичних характеристик черг пакетів у пункті А та у пункті В.

Розв’язання.

Об’єктом обслуговування є пакети даних, що передаються. Обслуговування здійснюють лінії зв’язку АВ1, АВ2, ВС1, ВС2. Кожній з ліній зв’язку поставимо у відповідність СМО: лінії АВ1 – СМО1, лінії АВ2 – СМО2, лінії ВС1 – СМО3, лінії ВС2 – СМО4.

СМО1 і СМО2, мають спільну чергу, в якій не може міститись більше 20 пакетів. Тому черга має обмеження 20 місць. Канал першої СМО, який відповідає лінії АВ1, обслуговує пакети з часом t_обр=20. Канал другої СМО, який відповідає лінії АВ2, обслуговує пакети з часом t_обр=20±5. Після обробки у першій СМО пакет надходить до третьої СМО. А після обробки в другій СМО пакет надходить до четвертої СМО. Сумарна кількість пакетів у чергах СМО3 і СМО4 - 25 пакетів. Канал третьої СМО відповідає лінії ВС1 і має параметр часу обслуговування:

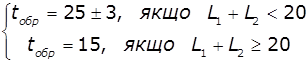
СМО4 відповідає лінії ВС2 і має параметр часу обслуговування:

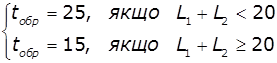
Пакети, які при надходженні у будь-яку СМО не знайшли вільного місця ні в каналі, ні в черзі, залишають мережу не обслугованими.

Пакети надходять в мережу МО з часом t_надх=10±5 до ліній зв’язку АВ1 та АВ2.

З’єднуємо побудовані СМО відповідно до маршруту пакетів і отримуємо мережу МО, що моделює процес передачі пакетів даних:

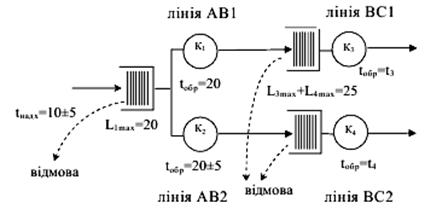
Завдання для індивідуального розв’язання

Задача 1. Складіть формалізовану модель системи засобами мереж масового обслуговування для наступної задачі:

Розглядається модель банку, у якому два касири сидять у приміщенні, а два обслуговують клієнтів, що під'їжджають на автомобілях. Частина клієнтів, що надходять у банк, намагається спочатку обслужитися у автомобільних касирів. Час між надходженнями клієнтів цих клієнтів має експоненціальний закон розподілу з математичним сподіванням 0,75 хвилини. У черзі до першого касира можуть знаходитись три автомобілі, а в черзі до другого – чотири. Час обслуговування першим автомобільним касиром нормально розподілено з математичним сподіванням 0,5 хвилини. Тривалість обслуговування другим касиром розподілена рівномірно на інтервалі 0,2…1,0 хвилини. Якщо клієнт, що приїхав на автомобілі, не може стати в чергу до автомобільних касирів через відсутність вільного місця, він залишає машину на стоянці і йде до касирів, що сидять у приміщенні банку. Інша частина клієнтів йде зразу на обслуговування до касирів у приміщенні банку і стають в одну чергу з клієнтами, що прибули на автомобілях. Інтервал між їхніми прибуттями розподілений за експоненціальним законом з математичним сподіванням 0,5 хвилини. До обох касирів стоїть одна черга. У черзі не може стояти більш 7 клієнтів. Клієнти, що прийшли в банк, коли черга заповнена повністю, не обслуговуються і залишають банк. Час обслуговування в обох касирів у помешканні банку має трикутний розподіл на інтервалі 0,1…1,2 хвилини.

Метою моделювання є визначення завантаження автомобільних касирів і касирів у банку, середніх довжини черг, а також ймовірності того, що клієнт піде з банку не обслугованим.

Задача 2. Складіть формалізовану модель системи засобами мереж масового обслуговування для наступної задачі:

У вузол комутації повідомлень, що складається з вхідного буфера, процесора, двох вихідних буферів і двох вихідних ліній, надходять повідомлення з двох напрямків. Повідомлення з одного напрямку надходять у вхідний буфер, обробляються в процесорі, буферуються у вихідному буфері першої лінії і передаються по вихідній лінії. Повідомлення з другого напрямку обробляються аналогічно, але передаються по другій вихідній лінії. Застосовуваний метод контролю потоків потребує одночасної присутності в системі не більш трьох повідомлень на кожному напрямку. Повідомлення надходять через інтервали 15±7 мс. Час обробки в процесорі дорівнює 7 мс на повідомлення, час передачі по вихідній лінії дорівнює 15±5 мс. Якщо повідомлення надходить при наявності трьох повідомлень у напрямку, то воно одержує відмову.

Метою моделювання є визначення завантаження процесора та вихідних ліній, визначення ймовірності відмови в обслуговуванні через переповнення буфера напрямку.

Задача 3. Складіть формалізовану модель системи засобами мереж масового обслуговування для наступної задачі:

На регулювальну ділянку цеху через випадкові інтервали часу надходять по два агрегати в середньому через кожні 30 хвилин. Первинне регулювання здійснюється для двох агрегатів одночасно і займає біля 30 хвилин. Якщо в момент приходу агрегатів попередня партія не була оброблена, агрегати на регулювання не приймаються. Агрегати, які одержали відмову, після первинного регулювання надходять у проміжний накопичувач. З накопичувача агрегати, що пройшли первинне регулювання, надходять попарно на вторинне регулювання, яке виконується в середньому за 30 хвилин, а ті, що не пройшли первинне регулювання, надходять на повне регулювання, що займає 100 хвилин для одного агрегату. Всі величини, задані середніми значеннями, мають експоненціальний розподіл.

Метою моделювання є визначення ймовірності відмови в первинному регулюванні, завантаження накопичувача агрегатами, що потребують повного регулювання.

Задача 4. Складіть формалізовану модель системи засобами мереж масового обслуговування для наступної задачі:

Філія банку з п’ятьма касами обслуговує клієнтів протягом робочого дня. Інтервали часу між надходженням клієнтів є випадкова величина, що має експоненціальний закон розподілу із середнім значенням 1 хвилина.

Час обслуговування клієнтів є випадкова величина, що має експоненціальний розподіл із середнім значенням 4,5 хвилини.

До кожної каси формується окрема черга. Клієнт, що надійшов на обслуговування, обирає найкоротшу чергу.

В зв’язку з тим, що керівництво банку цікавлять поточні витрати та якість послуг, що надаються клієнтам, ставиться питання про можливість зменшення кількості кас.

Задача 5. Складіть формалізовану модель системи засобами мереж масового обслуговування для наступної задачі:

На складальну ділянку цеху підприємства через інтервали часу, що мають експоненціальний закон розподілу з середнім значенням 10 хвилин, надходять партії, кожна з який складається з трьох деталей. Половина всіх деталей, що надходять, перед зборкою повинна пройти попередню обробку протягом 7 хвилин На зборку подаються оброблена і необроблена деталі. Процес зборки займає усього 6 хвилин Потім виріб надходить на регулювання, що продовжується в середньому 8 хвилин (час виконання має експоненціальний розподіл). У результаті зборки можлива поява 4% бракованих виробів, що не надходять на регулювання, а направляються знову на попередню обробку.

Метою моделювання є визначення можливих місць появи черг та їхніх статистичних характеристик, середньої та максимальної кількість деталей, що находиться на складальній ділянці цеху.