Практична робота № 10
одноканальні СМО
Мета: навчитись розраховувати
основні параметри одноканальних систем масового
обслуговування.
Основні теоретичні відомості
Класифікація систем
масового обслуговування. По числу обслуговуючих каналів
СМО поділяються на:
·
Одноканальні СМО - СМО з одним каналом обслуговування.
·
Багатоканальні - СМО з
декількома каналами обслуговування.
За часом перебування вимог в черзі до початку обслуговування
·
СМО з відмовами - це СМО, в
якій заявка, що поступає в момент, коли всі канали зайняті, дістає відмову,
покидає СМО і надалі в процесі обслуговування не бере участь (наприклад,
телефонна мережа, в якій заявка на телефонну розмову покидає СМО у випадку,
коли канал зайнятий.).
·
СМО з чеканнями (чергою) - це
СМО, в якій заявка, що прийшла в момент, коли всі канали зайняті стає в чергу
на обслуговування. У свою чергу СМО з чеканням (чергою) підрозділяються на:
-
СМО з обмеженою чергою.
-
СМО з необмеженою чергою.
-
СМО з обмеженим часом чекання
(вимога, що поступила, заставши всі пристрої зайнятими, стає в чергу і чекає
обслуговування протягом обмеженого часу. Не діждавшись обслуговування у
встановлений час, вимога покидає систему).
-
СМО з необмеженим часом
чекання.
Розглянемо роботу і основні характеристики
одноканальних СМО, тривалість обслуговування в яких -
випадкова величина, підпорядкована показниковому
закону розподілу. Потік обслуговування є простим пуассонівським
потоком подій.
Показники ефективності таких СМО:
А - абсолютна пропускна спроможність СМО;
Q - відносна пропускна спроможність;
Рвідм - імовірність відмови;
Lсист - середнє число заявок, що знаходяться в системі;
Тсист - середній час перебування заявки в системі;
Lч - середня довжина черги;
Тч - середній час чекання в черзі.
Одноканальна СМО з відмовами
Є один канал, на який поступає потік
заявок з інтенсивністю λ. Потік обслуговування має інтенсивність μ.
Розмічений граф станів представлений на рис.1.
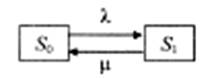
Рис.1. Граф станів
одноканальної СМО з відмовами
Канал може перебувати в двох станах:
S0 - канал обслуговування вільний;
S1 - канал обслуговування зайнятий.
Граничні імовірності станів виражають
середній відносний час перебування системи в стані S0 та S1, тобто визначають відносну
пропускну здатність системи та імовірність відмови:
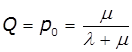 ,
, 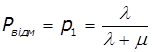 ,
,
Тоді абсолютна пропускна здатність
системи:
![]() .
.
Приклад
У перукарні працює один майстер. Час
обслуговування клієнта розподілений по показниковому
закону з середнім значенням 12 хв. Клієнт, що прийшов в перукарню, коли майстер
зайнятий, не чекає обслуговування, а покидає перукарню. Потік клієнтів -
простий з інтенсивністю 8 клієнтів/год. Знайти показники ефективності роботи
даної перукарні.
Рішення.
Маємо λ=8 (кл/год.),
середній час обслуговування to6.с = 12(хв)= 0,2(год). Отже, інтенсивність
потоку обслуговування μ=1/ to6.с = 5.
Тоді відносна пропускна спроможність
Q=0,38, тобто в середньому 38% клієнтів, що поступають, будуть обслужена.
Відповідно вірогідність відмови в обслуговуванні складе Рвідм=0,62
(тобто 62 %). Абсолютна пропускна спроможність СМО А=8 0,38=3,04, тобто в
середньому в годину буде обслужено 3 клієнти.
Одноканальна СМО з обмеженою довжиною черги
Розглянемо одноканальну систему масового
обслуговування з чеканням, в яку поступає простий потік заявок з інтенсивністю
λ; інтенсивність обслуговування μ (тобто в середньому безперервно
зайнятий канал видаватиме ![]() обслужених заявок в
одиницю часу). Заявка, що поступила в мить, коли канал зайнятий стає в чергу і
чекає обслуговування. Передбачимо, що кількість місць в черзі m, тобто якщо
заявка прийшла в мить, коли в черзі вже стоять m-заявок, вона покидає систему
не обслуженою.
обслужених заявок в
одиницю часу). Заявка, що поступила в мить, коли канал зайнятий стає в чергу і
чекає обслуговування. Передбачимо, що кількість місць в черзі m, тобто якщо
заявка прийшла в мить, коли в черзі вже стоять m-заявок, вона покидає систему
не обслуженою.
Розмічений граф станів представлений на
рис.2.

Рис.2. Граф станів
одноканальної СМО з обмеженою довжиною черги
So - канал обслуговування вільний;
S1 - канал обслуговування зайнятий, але
черги немає;
S2 - канал обслуговування зайнятий, в
черзі стоїть 1 заявка;
Sm - канал обслуговування зайнятий, в черзі всі m заявок, будь-яка
наступна заявка дістає відмову.
Вірогідність станів визначається рівняннями:
![]()
Якщо ![]() , то
, то 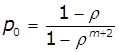
Якщо ![]() , то
, то ![]() .
.
Тоді: ![]() ,
, ![]() , …,
, …, ![]()
![]()
![]() ,
, ![]()
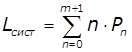 ,
, ![]()
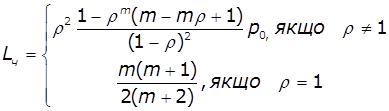
![]()
Приклад.
Автозаправна станція (АЗС) є СМО з одним каналом обслуговування
(однією колонкою). Майданчик при станції допускає перебування в черзі на заправку
не більше п'яти машин одночасно (m = 5). Якщо в черзі вже знаходяться п'ять
машин, наступна машина в чергу не стає. Потік машин, що прибувають для
заправки, має інтенсивність λ = 2 (машини в хвилину). Інтенсивність потоку
обслуговування складає μ = 2.
Рішення.
![]() , тоді
, тоді ![]() - імовірність вільної СМО.
- імовірність вільної СМО.
![]() , звідси
, звідси ![]() .
.
![]() - відмовляють кожному
7 клієнту.
- відмовляють кожному
7 клієнту.
![]() ,
, ![]() маш/хв.
маш/хв.
Середнє число заявок і час перебування
машини в системі:
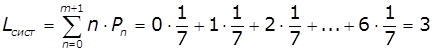 ,
,
![]() хв.
хв.
Середня довжина і час перебування в
черзі:
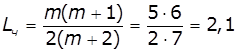 маш.
маш. ![]() хв.
хв.
Одноканальна СМО з необмеженою довжиною черги
Розглянемо одноканальну систему масового
обслуговування з необмеженою чергою, в яку поступає простий потік заявок з
інтенсивністю λ і інтенсивністю обслуговування μ. Заявка, що
поступила в мить, коли канал зайнятий, стає в чергу і чекає обслуговування.
Розмічений граф станів представлений на
рис. 3.

Рис. 3. Одно канальна
СМО з необмеженою довжиною черги
So - канал обслуговування вільний;
S1 - канал обслуговування зайнятий, але
черги немає;
S2 - канал обслуговування зайнятий, в
черзі стоїть 1 заявка;
Sm - канал обслуговування зайнятий, в черзі всі m заявок,
…
Оскільки немає обмеження на довжину
черги, то відмов немає:
![]() ,
, ![]() .
.
Тоді:![]()
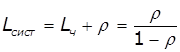 ,
, ![]()
![]() ,
, ![]()
Якщо λ>μ, то черга буде
постійно збільшуватись.
Приклад.
У перукарні працює один майстер. Інтенсивність потоку клієнтів складає
4 клієнти в годину. Інтенсивність обслуговування - 5 клієнтів в годину.
Передбачається, що черга може бути необмеженої довжини. Визначити показники
ефективності роботи перукарні і імовірність того, що чекають своєї черги не
більше трьох клієнтів.
Рішення.
Інтенсивність потоку обслужених заявок ![]() , тоді гранична імовірність того, що перукар простоює:
, тоді гранична імовірність того, що перукар простоює: ![]() , а імовірність того , що він зайнятий
, а імовірність того , що він зайнятий ![]() .
.
Імовірність того, що в черзі не більше трьох клієнтів:
![]() , де:
, де:
![]() ,
, ![]() ,
, ![]()
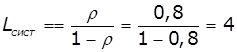 чол.,
чол., ![]() год.
год.
Черга: 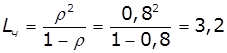 чол.,
чол., ![]() год.
год.
Завдання для індивідуального
розв’язання.
1.
Розглядається цілодобова
робота пункту СТО автомашин з одним каналом. На огляд кожної машини витрачається
в середньому 0,5 години. На СТО поступає в середньому 36 машин за добу. Якщо
машина прибуває, коли пункт огляду зайнятий, вона покидає його не обслуженою.
Визначити граничну імовірність станів і характеристики обслуговування СМО.
2.
На вхід однієї телефонної лінії поступає
простий потік викликів з інтенсивністю 0,4 викликів/хв. Середня тривалість
розмови 3 хв. Знайти граничну імовірність станів і характеристики
обслуговування СМО. Порівняти пропускну спроможність СМО з номінальною, яка
була б, якщо розмова тривала 3 хв, а виклики йшли б один за другим регулярно,
без перерв.
3.
Закусочна на АЗС має один прилавок. Автомобілі
прибувають випадковим чином, в середньому 2 автомобілі за 5 хвилин. Для
виконання замовлення в середньому досить 1.5 хвилини. Знайдіть: а) імовірність
простою прилавка; б) середні характеристики; з) імовірність того, що прибуде не
менше 5 автомобілів.
4.
У магазині встановлено, що потік покупців є
простим з інтенсивністю 1 покупець в хвилину. У цьому магазині встановлений
один касовий апарат, середній час обслуговування одного клієнта складає
приблизно 1,25 хв. Визначити характеристики СМО за умови, що черга обмежена
контролером при вході в зал самообслуговування: m = 3 покупці.
5.
На автомийці
влаштовано один блок для обслуговування і є одне місце для черги. Автомобілі
прибувають з інтенсивністю 5 авто/година. Середній час обслуговування однієї
машини - 10 хвилин. Знайдіть всі середні характеристики СМО.
6.
Платна стоянка для легкових
машин має 7 місць. Знайдіть імовірність того, що нова машина знайде вільне
місце, якщо машини в середньому прибувають через 10 хв. а займають місце на
стоянці в середньому 1 год.
7.
У одноканальну СМО поступають заявки з
інтенсивністю 0,85 заявок в годину. Час обслуговування заявки в середньому рівний
1,05 години. Черга може зростати практично необмежено. Знайдіть показники
ефективності роботи СМО.
8.
У порту є один причал для розвантаження
кораблів. Інтенсивність потоку суден дорівнює 0,4 (суден в добу). Середній час
розвантаження одного судна складає 2 доби. Передбачається, що черга може бути
необмеженої довжини. Знайти показники ефективності роботи причалу, а також
імовірність того, що чекають розвантаження не більше ніж 2 судна.